d라이브러리

수학의 재미를 알리기 위해 앞장서는 사람이 있습니다. 바로 2022 릴라바타상 수상자 니콜라이 안드레예프 러시아 스테클로프 수학연구소의 수학 대중화연구소 소장인데요. 안드레예프 소장은 2002년부터 수학 에뛰드라는 홈페이지를 만들어 수학 대중화에 힘쓰고 있습니다. 그의 이야기를 7월 4일 핀란드에서 들었습니다. 

Q. 대중에게 수학을 널리 알린 사람에게 주는 릴라바티상을 받으셨습니다. 수상 소감을 듣고 싶어요.

2002년도부터 시작한 ‘수학 에뛰드’라는 프로젝트로 릴라바티상을 받았습니다. 상을 받은 것 자체보다는 제 일이  수학의 대중화에 도움이 된다는 것에 기쁩니다. 러시아에 있는 많은 선생님들이 수업에서 제가 만든 홈페이지의 애니메이션을 사용하면서 학생들을 가르친다고 하니까요.

Q. ICM이 자국인 러시아에서 개최되는 것에 대해 기대감을 보이셨는데, 취소돼 아쉬우실 것 같아요.

당연히 ICM이 러시아에서 열렸으면 했어요. ICM에서 할 수학 대중화 행사도 계획 중이었지요. 러시아에서 지난 1964년에 ICM이 열린 뒤, 다시 얻은 기회였는데 좋은 기회를 날린 것 같아서 너무 애석해요. 대회를 유치하기 위해 많은 사람들이 노력하고 기대했는데 정말 아쉽습니다.

Q. 어떤 계기로 수학 에뛰드를 시작하게 됐나요?

수학 대중화연구소에서 일하게 되면서 처음으로 수학 대중화 활동이 있다는 걸 알았어요. 그러던 중 많은 사람에게 수학 원리를 시각화해 소개하면 좋겠다고 생각했지요. 이렇게 만들었던 영상들이 선생님과 학생들에게 굉장히 좋은 반응을 얻어서 계속하고 있어요.

Q. 수학 에뛰드에 대해 설명해 주세요!

수학 에뛰드는 3D 애니메이션을 활용해 수학을 이해하기 쉽고, 흥미롭게 보여주려고 만든 홈페이지예요. 수학 원리가 담긴 여러 사례를 수집해서 3D 애니메이션으로 만들고 짧은 글로 원리를 설명합니다. 3D 애니메이션을 활용하면 직관적이고 명확하게 이해할 수 있다는 장점이 있어요. 어린 아이들도 흥미를 느끼고요.

Q. 3D 애니메이션을 만들 때 한국 홈페이지를 참고하셨다고 들었는데 어떤 홈페이지인가요?

전 세계적으로 수학의 대중화에 대한 사례가 많지 않아요. 그래서 검색하다가 한국의 ‘수학사랑’이라는 홈페이지를 발견했어요. 이 홈페이지를 보면서 여러 수학을 3D 애니메이션으로 만들 수 있겠다고 생각했어요.

3D 애니메이션으로 맛보는 수학! 수학 에뛰드

[감자칩이 길다란 구멍을 통과할까?]

원통에 들어 있는 감자칩을 먹어 본 적 있나요? 이 감자칩을 자세히 들여다보면 말 안장 모양인 ‘쌍곡포물면’ 형태를 띠고 있어요. 쌍곡포물면은 z축에 수직인 평면으로 자르면 쌍곡선, x축과 y축에 수직인 평면으로 자르면 포물선이 생기는 특징이 있어요.

그렇다면 여기서 문제! 감자칩 통 뚜껑에 길다란 직선 모양의 구멍을 내고 감자칩이 깨지지 않도록 통과시킬 수 있을까요? 쌍곡포물면은 직선의 연속적인 움직임으로 면을 이뤄지기 때문에 감자칩을 돌려 가며 넣어주면 깨지지 않고 구멍을 통과할 수 있답니다.

[소시지로 삼각함수를 그리자!]

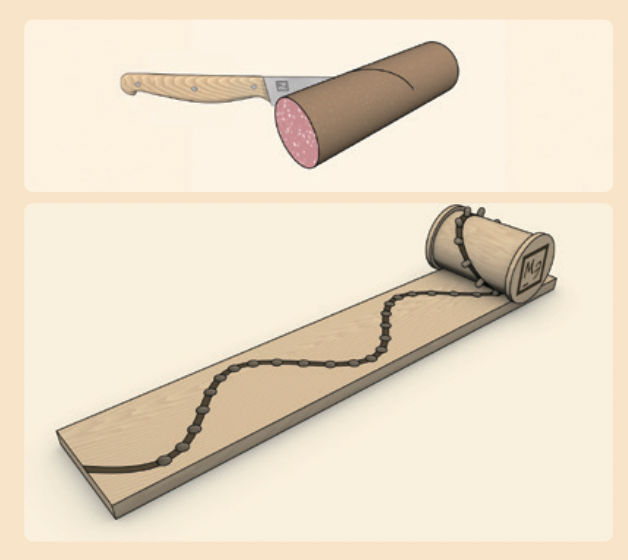
집에 있는 소시지를 이용해 삼각함수를 그려 봅시다. 먼저 원통형 소시지를 비스듬히 45로 잘라요. 그 뒤 길다란 정사각형 모양 판 위에 일직선으로 굴리며 소시지의 자른 부분과 바닥이 닿는 점의 자취를 따라 그려 보세요. 오르락내리락하는 선이 그려질 텐데요. 이때 소시지의 반지름이 1이라면 놀랍게도 삼각함수 y = sinx 그래프와 일치합니다!

소시지의 굵기나 잘린 각도가 달라도 삼각함수로 나타낼 수 있어요. 반지름이 r이라면 y = rsinx 그래프와 같고, 자르는 각도가 45˚가 아닌 α라면 y = tanα×sinx 그래프로 표현할 수 있답니다.

[원기둥 = 원뿔 + 반구]

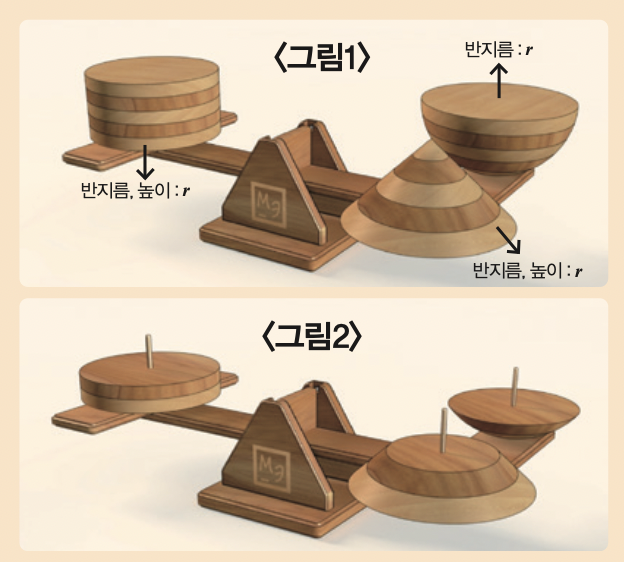
고대 그리스 수학자 아르키메데스는 반지름, 높이가 r로 같은 원기둥과 반지름이 r인 구의 부피 비는 3 : 2라는 사실을 밝혔습니다. 후대 학자들은 반지름과 높이가 r인 원기둥과 밑면의 반지름과 높이가 r인 원뿔의 부피 비는 3 : 1임을 발견했지요.

이 사실을 이용해 양팔 저울 실험을 해 봅시다. 우선 저울의 한 쪽 팔에 높이와 반지름이 r인 원기둥을 놓아요. 다른 쪽 팔엔 높이와 반지름이 r인 원뿔과 반지름이 r인 반구를 놓으면 균형이 맞아요<;그림1>;. 놀라운 점은 세 도형의 높이를 5등분해서 맨 아래 두 조각만 놓아도 여전히 균형이 맞습니다<;그림2>;.

[삼각형 하나로 축구공 만드는 방법]

1970년 멕시코 월드컵 공인구인 ‘텔스타 축구공’은 검은색 정오각형 12개와 흰색 정육각형 20개로 구성된 깎인 정이십면체입니다.

정삼각형 종이와 거울만 있으면 텔스타 축구공을 만들 수 있어요. 우선 한 변의 길이가 3cm인 정삼각형 종이의 세 꼭짓점을 한 변의 길이가 1cm인 정삼각형 모양으로 색칠해요. 그 뒤 두 변의 길이가 9.5cm이고, 밑변이 10cm인 이등변삼각형 모양 거울 3개를 삼각뿔 형태로 붙입니다.

이제 정삼각형 종이를 삼각뿔 형태의 거울 중앙에 붙이면 축구공이 나타납니다. 거울 3개가 모여 삼각형을 비추기 때문에 시선을 움직여도 공 형태가 바뀌지 않아요.