알고 싶은 정보가 2개 이상일 때 연립방정식을 이용하게 되는데요.
오늘은 일차방정식과 일차함수의 관계를 이용해서 미지수가 2개인 연립일차방정식의 해를 구하는 문제들을 살펴볼게요!

중학교 2학년 문자와 식 단원 ‘일차함수와 일차방정식의 관계’에서는 실생활의 다양한 문제를 만나볼 수 있어요. 어떤 유형의 문제가 있는지 살펴보고 해를 구하는 방법을 알아볼게요.
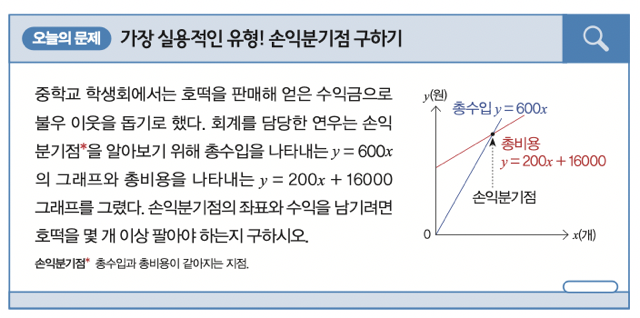
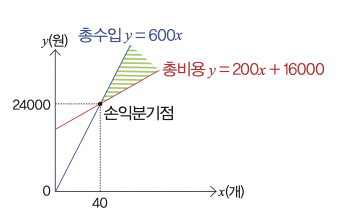
STEP 1. 두 일차방정식을 연립해 손익분기점 구하기
일차함수의 그래프와 일차방정식의 그래프가 같아요. 좌표평면에 그려진 두 일차함수를 미지수가 2개인 일차방정식의 형태로 나타내 보세요.

이 두 함수를 일차방정식으로 나타낸 뒤 연립하면, 두 식을 모두 만족하는 x, y의 값을 구할 수 있어요.
두 일차방정식의 y의 계수가 -1로 같으므로 ㉠ - ㉡을 하면
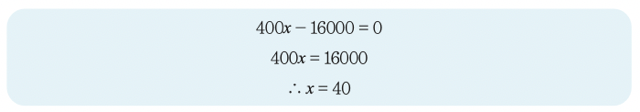
y = 600x 식에 x = 40을 대입하면 y = 24000이에요. 따라서 연립일차방정식의 해는 x = 40, y = 24000입니다. 손익분기점의 좌표는 두 일차방정식의 그래프의 교점의 좌표이므로 (40, 24000)임을 알 수 있어요.
STEP 2. 이익을 얻기 위한 판매량을 그래프로 구하기
호떡을 팔아 이익을 얻으려면 손익분기점에서의 판매량보다 많이 팔아야 하므로 호떡을 41개 이상 팔아야 수익을 남길 수 있어요.