d라이브러리

1931년 오스트리아 출신 미국 수학자 쿠르트 괴델이 발표한 ‘불완전성 정리’는 모순 없는 공리계를 만들고자 노력한 수학자들의 희망을 앗아가 버렸습니다. 그 이유가 무엇인지 알아봅시다.

♥ 증명할 수 없는 문장

괴델의 불완전성 정리는 제1정리와 제2정리로 구성돼 있습니다. 두 정리 중 특히 제2정리는 모순 없는 공리계를 구축하고자 한 ‘힐베르트 프로그램’을 정면으로 반박하는 내용입니다. 제2정리의 증명은 제1정리의 증명으로부터 유도되므로, 이 글에서는 제1정리의 증명을 중점적으로 살펴볼게요.

S를 모순이 없는 어떤 수학 체계라고 합시다. 괴델은 만약 S가 아래와 같은 문장 p를 허용하는 수학 체계라면 어떤 일이 벌어질지를 생각해 봤어요.

p가 거짓이라고 가정하면 p는 증명이 가능합니다. S가 모순이 없는 체계라면 증명 가능한 명제는 참이어야 합니다. 그런데 이는 p가 거짓이라는 가정에 위배됩니다. 결국 p는 참이어야 하고, 이는 p가 참이지만 증명할 수 없는 명제임을 의미합니다.

물론 그렇다고 괴델의 제1정리가 증명된 것은 아닙니다. 왜냐하면 p는 수학의 언어로 적힌 문장이 아니기 때문이지요. p는 일상 언어의 불완전성을 보여 줄지언정, 수학 체계의 불완전성을 보여 주지는 않습니다. 따라서 우리가 수학 체계의 불완전성을 보이고 싶다면 문장 p를 수학의 언어로 번역해야 합니다.

그런데 많은 수학자는 이것이 불가능하다고 생각했습니다. 수학의 언어는 기껏해야 숫자와 기호뿐인데, 단순한 기호들로부터 p같은 문장이 만들어지지는 않아 보였거든요. 때문에 힐베르트 프로그램의 지지자들은 이 문제를 심각하게 고려하진 않았습니다.

그런데 충격적이게도 괴델이 자연수를 포함하는 모든 수학 체계에서는 문장 p를 구성할 수 있다는 사실을 증명해 버린 겁니다.

♠ ‘괴델 수’로 번역하기

괴델은 문장 p를 수학의 언어로 바꾸기 위해서 ‘괴델 수’라는 독창적인 아이디어를 고안했습니다. 괴델 수는 문장을 자연수로 변환하는 기술입니다. 마치 컴퓨터가 한국어 문장을 0과 1의 나열로 변환해서 저장하듯이 말이죠. 그러면 괴델이 컴퓨터에서 영감을 얻은 거냐고요? 사실은 정반대입니다. 1936년 영국 수학자 앨런 튜링이 괴델의 이 증명에서 착안해 0과 1로 모든 문장을 표현하는 컴퓨터를 처음 떠올렸거든요.

수식을 자연수로 변환하는 과정은 다음과 같습니다. 먼저 모든 수학 기호마다 고유한 자연수를 부여합니다. 여기에서는 편의상 수학 기호가 ‘+, =, 1, 2’만 있다고 가정할게요.

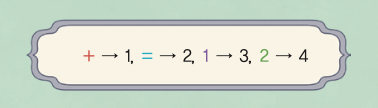
이 대응 관계를 가지고서 ‘1 + 1 = 2’를 자연수로 변환해 보겠습니다. 먼저 이 식에 등장하는 5개의 기호를 모두 괴델 수로 바꿉니다. 그러면 3, 1, 3, 2, 4를 얻습니다. 이 5개의 자연수를 가장 작은 소수부터 차례대로 각 지수로 삼은 뒤 이를 모두 곱합니다. 그러면 2,152,227,000이라는 큰 수를 얻는데요, 이 수가 바로 1 + 1 = 2를 자연수로 변환한 결과입니다. 이것을 1 + 1 = 2의 괴델 수라고 불러요.

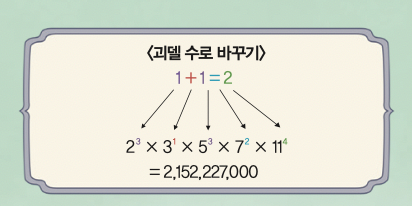
이 과정을 따르면 모든 수식은 고유한 괴델 수를 가지게 됩니다. 또한 괴델 수를 소인수분해 하면 이 괴델 수가 어떤 수식을 의미하는지도 알아낼 수 있지요. 괴델 수를 사용하면 다양한 문장을  수학의 언어로 바꿀 수 있어요. 괴델 수 덕분에 표현력이 어마어마해진 겁니다. 물론 그 과정은 정말 난해하고 까다롭지만요. 괴델은 그의 논문에서 이 과정을 실제로 수행해 보였습니다. 이로써 자연수를 포함하는 수학 체계에서는 참이지만 증명이 불가능한 명제가 존재함이 보여졌지요.

앞에서 제2정리는 제1정리로부터 유도된다고 언급했는데요, 그 아이디어를 아주 간략하게 소개해 볼게요. 이제부터 할 이야기는 정말 수수께끼 같으니 헷갈리지 않도록 주의해야 합니다.

만약 수학 체계 S가 스스로 모순적이지 않다는 사실을 증명할 수 있다면, 다음의 문장 a를 증명하는 것이 가능하다는 의미입니다.

문장 b도 증명이 가능합니다. 그러나 만약 문장 a가 증명 가능하다면, 문장 b에 의해 ‘문장 p는 증명할 수 없다’가 증명됩니다. 그런데 괴델의 제1정리에 의해 ‘문장 p는 증명할 수 없다’는 증명할 수 없는 문장입니다. 이는 모순이므로, 문장 a는 증명이 불가능합니다. 따라서 수학 체계는 스스로 모순적이지 않다는 사실을 증명할 수 없습니다.