d라이브러리

러셀의 역설이 발표되자 수학자들은 이 골칫거리를 제거하기 위해 수학 체계를 수정하고자 했습니다.
그런데 수학 체계를 수정한다는 것이 정확히 무슨 의미일까요?

♥ 수학 = 언어

이론적인 측면에서 보면 수학은 고도로 정교한 언어와 크게 다르지 않습니다. 따라서 언어가 어떻게 작동하는지를 이해하면 수학이 어떻게 작동하는지 또한 쉽게 알 수 있어요.

한국어를 예로 들어 볼게요. 한국어는 한글이라는 문자와 한글을 어떻게 조합할 수 있는지를 규정하는 문법으로 이뤄져 있어요. 한국어 문법에 따르면 ‘나는 사과를 먹는다’는 맞는 문장이지만, ‘먹는다 나는 사과를’은 틀린 문장입니다.

수학도 마찬가지예요. 문자와 문법을 가지고 있죠. 수학의 문자는 기호나 숫자입니다. 수학 문법에 따르면 ‘x ∈ A(x는 A에 속한다)’는 맞는 식이지만, ‘Ax ∈’는 틀린 식이에요. 수학자들은 이런 수학 문법을 ‘공리계’라고 부릅니다. 공리란 증명이 필요하지 않은 명제로 어떤 이론의 기반을 가리키는 말인데, 이 명제들을 하나로 묶은 것이 바로 그 이론의 공리계예요.

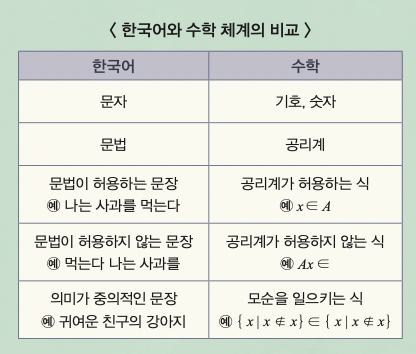
그런데 한국어 문법이 허용하는 문장 중에는 중의적 문장이 있습니다. 이처럼 ‘귀여운 친구의 강아지’라는 문장은 ‘친구가 귀엽다’는 의미일 수도 있고, ‘친구의 강아지가 귀엽다’는 의미일 수도 있어요. 만약 한국어에서 이런 중의적 문장이 나올 가능성을 완전히 없애고 싶다면 어떻게 해야 할까요?

네, 한국어 문법을 수정해야 합니다. 예를 들어 ‘형용사는 바로 오른쪽에 위치한 명사를 수식한다’라는 법칙을 한국어 문법에 추가한다면 친구가 귀엽다는 의미만 있겠지요.

실제로 1987년 논리학자와 언어학자들은 중의적 문장이 없는 인공 언어를 만들기 위해 ‘로지반(Lojban)’이라는 인공 언어를 만드는 ‘로지반 프로젝트’를 진행했어요. 이후 로지반에는 중의적 문장이 없다는 사실을 수학적으로 증명해 밝혔지요.

♠ 모순 없는 체계 만들기

20세기 수학계에서도 로지반 프로젝트와 비슷한 움직임이 일어났습니다. 기존 수학의 공리계는 아래와 같이 모순을 일으키는 식을 허용했기 때문에 문제가 있었어요.

오, 뭔가 엄청 어려워 보이는 식이 등장했는데요, ‘자기 자신을 포함하지 않는 집합들의 집합은 자기 자신을 포함한다.’ 지난 호를 보신 분들은 익숙한 문장이라고 여기실 텐데요. 네, 맞습니다. 우리가 4월호에서 살펴본 러셀의 역설이에요! 위 명제는 참임을 증명할 수도 있고 거짓임을 증명할 수도 있습니다.  따라서 { x | x ∉ x } ∈ { x | x ∉ x }와 같은 식을 허용하는 공리계는 문제가 있어요. 이에 수학자들은 수학에서 모순을 일으키는 식을 제거하기 위해 새로운 공리계를 만들고자 했습니다. 마치 로지반 제작자들이 언어에서 중의적 문장을 제거하기 위해 새로운 언어 체계를 만들었듯이 말이죠.

♣ 모순 안녕!

이 작업에 누구보다 앞장섰던 사람은 바로 독일의 수학자 다비트 힐베르트입니다. 그는 ‘힐베르트 프로그램’이라는 이름으로 수많은 수학자와 함께 모순 없는 공리계를 구축하고자 했어요. 야심찬 프로젝트였고, 많은 진전도 있었습니다. 1930년 오스트리아 수학자 쿠르트 괴델이 ‘1차 논리에서 참인 명제를 항상 증명할 수 있다’는 ‘완전성 정리’를 증명함으로써, 1차 논리라는 단순한 수학 체계에서는 모순이 없다는 사실을 보였습니다.

1차 논리란 명제에서 대상에 대해서만 ∀(= 모든 ~에 대해), ∃(= 어떤 ~가 존재하여) 같은 기호를 붙여 한정할 수 있고, 술어는 한정하지 않는 논리 체계예요. 대상은 명제가 적용되는 주인공을 말하며, 술어는 대상에 대한 속성(개념), 관계 등을 말하는데요. 예를 들면 1차 논리에서는 ‘모든 x가 치킨을 좋아한다’라는 명제가 허용됩니다.

안타깝게도 1차 논리는 너무 단순하기 때문에 자연수를 가장 기초 개념으로 보고 수학의 개념을 확장해 나가는 자연수 이론을 구성할 수 없어요. 그러나 많은 수학자는 완전성 정리를 발판 삼아 자연수 이론까지 구성할 수 있는, 모순 없는 수학 체계도 머지않아 발견할 것이라고 생각했죠. 그리고 정말로 이듬해 괴델이 완전성 정리보다 더 놀라운 정리를 발견했다는 사실이 전해지자 수학계는 다시 한번 떠들썩해졌습니다.