d라이브러리

20세기 수학계를 아수라장으로 만들어 버린 역설이 있어요.

당시 수학계에서는 수학의 기초를 세우기 위한 작업이 한창 이뤄지고 있었는데, ‘러셀의 역설’이 이 야심 찬 작업을 송두리째 뒤흔들어 놓았기 때문이에요. 대체 무슨 일이 있었던 걸까요?

수학 블록 1층은 자연수 이론?

수학에는 다양한 개념이 있습니다. 이 중 대부분은 조금 더 기초적인 개념으로부터 확장된 것입니다. 예를 들어 평면좌표는 실수로부터 나온 것입니다. 평면좌표는 실수 2개를 연달아 쓴 것이기 때문이지요. 실수는 어떨까요? 엄밀한 의미에서 실수는 유리수로 이뤄진 ‘코시 수열’로 정의돼요. 말이 조금 어려운데, 일단은 코시 수열을 이용하면 유리수로 무리수를 구성할 수 있어서 유리수만으로도 실수를 구성할 수 있다는 사실만 알아두세요. 그런데 유리수는 정수/0이 아닌 정수여서 정수로 구성할 수 있어요. 그렇다면 정수는요? 정수는 (자연수) - (자연수)입니다. 따라서 정수는 자연수로부터 나온 것이지요.

이처럼 수학의 이론들은 ‘블록 쌓기’와 같은 형태로 이뤄져 있습니다. 복잡한 수학 이론은 더 단순한 수학 이론에 의해 뒷받침되지요. 그렇다면 블록들의 맨 밑바닥에는 무엇이 있을까요? 수학의 모든 이론을 지탱하는 가장 기초적인 이론은 무엇일까요? 19, 20세기의 수학자들은 이 질문에 대한 답을 찾고자 고군분투했어요.

어떤 수학자들은 ‘자연수 이론’이 블록의 1층이라고 생각했습니다. 1 + 1 = 2와 같은 자연수 이론은 증명이 불가능하며, 그저 자명한 것으로 인정해야 한다고 여겼어요. 그러나 많은 수학자는 자연수 이론을 증명 없이 받아들여야 하는 수학의 기반으로 보는 입장에 반대했습니다. 특히 논리주의 학파는 수학의 기반이 ‘논리학’이라고 생각했어요.

‘집합’으로 자연수 이론 증명?

논리주의를 처음으로 진지하게 주장한 학자는 독일의 수학자이자 논리학자인 고틀로프 프레게입니다. 프레게는 당시 태동하던 ‘집합’ 개념을 사용해서 자연수 이론을 증명하고자 했습니다. 집합이란 특정 대상들의 모임으로, 집합을 구성하는 각각의 대상을 ‘원소’라고 해요. 예를 들어 {에펠탑, 루트2, apple}은 3개의 원소로 이뤄진 집합입니다.

집합으로 이뤄진 집합도 생각할 수 있습니다. 예를 들어 { {1, 2, 3}, {사과, 바나나} }는 2개의 집합으로 이뤄진 집합이지요. 이런 집합의 크기는 무한할 수 있습니다. 모든 짝수의 모임은 원소 개수가 무한한 ‘무한집합’이에요.

프레게는 집합이 자연수를 정의하는 데 최적의 개념이라고 생각했습니다. 자연수를 일일이 세지 않아도 두 집합의 크기 비교가 가능하기 때문이지요. 예컨대 여러분이 숫자를 3까지 셀 줄 모른다고 해 봅시다. 두 집합 A, B에는 원소가 각각 3개씩 있어요. 개수를 셀 수 없기 때문에 두 집합의 원소를 하나씩 짝짓습니다. 그러면 원소를 남김없이 서로 짝지을 수 있다는 사실로부터 두 집합의 크기가 같다고 결론 내릴 수 있지요.

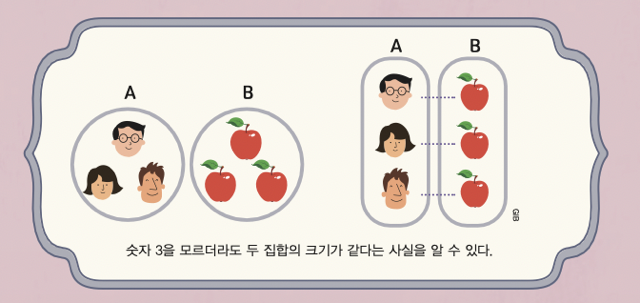
비록 ‘3’이라는 개념을 모르더라도 집합 A와 B가 동일한 크기라는 사실은 알 수 있습니다. 나아가 집합 A와 동일한 크기의 집합들로 이뤄진 집합 또한 구성할 수 있습니다. 프레게에 따르면 바로 이 집합이 자연수 3의 정의입니다.

이처럼 집합을 이용해 자연수를 정의한 뒤, 프레게는 집합과 논리학의 법칙을 이용해 자연수의 모든 성질을 증명해 냈습니다. 1+1=2나 2×3=6은 물론 2+3=3+2=5라는 ‘덧셈의 교환법칙’ 등 산술의 기본 법칙도 모두 증명했지요. 프레게는 이 모든 업적을 무려 600쪽에 달하는 <;산술의 기본 법칙>;이라는 책에 담았습니다. 이로써 논리학이야말로 증명 없이 인정해야 하는 수학의 기반이라는 사실이 입증되는 것처럼 보였습니다. 그러나

러셀, 프레게의 자연수 이론을 무너뜨리다

<;산술의 기본 법칙>; 2권 출판을 앞두고 프레게는 버트런드 러셀이라는 영국의 젊은 수학자로부터 편지를 받았습니다. 바로 이게 ‘러셀의 역설’로 불리는 내용이지요. 프레게는 대수롭지 않게 편지를 읽기 시작했지만, 편지를 다 읽자 바닥에 주저앉을 수밖에 없었습니다. 편지에서 러셀은 프레게의 집합에 큰 모순이 있다는 사실을 지적했거든요. 당황한 프레게는 서둘러 모순을 고치고자 다양한 방법을 찾아봤지만, 결국 모순을 고치지 못하고 자연수 이론의 증명을 포기할 수밖에 없었습니다. 절망한 그는 <;산술의 기본 법칙>; 2권 출판을 없었던 일로 하려고 했지만, 출판사의 설득 끝에 2권을 출판하되 다음과 같은 주석을 책 끝에 남겼습니다.