d라이브러리

색종이 하면 정사각형 모양의 종이가 먼저 떠오르지요? 이번엔 색다르게 원 모양의 색종이로 항상 2시 24분을 가리키는 시계를 만들어 보겠습니다. 어떻게 정확히 그 시각을 가리키는지 그 비밀부터 파헤쳐 볼게요.

정오각형에서 찾은 시각

2시 24분을 가리키는 시계를 상상해 보자. 시침은 2와 3 사이, 분침은 4와 5 사이를 5등분하는 눈금 중 5에 한 눈 금 못 미친 곳에 위치한다. 만약 이런 시계를 만들어야 한다면 시침과 분침이 이루는 각의 크기를 정확하게 알아야 한다. 정오각형에서 그 각도의 비밀을 찾을 수 있다.

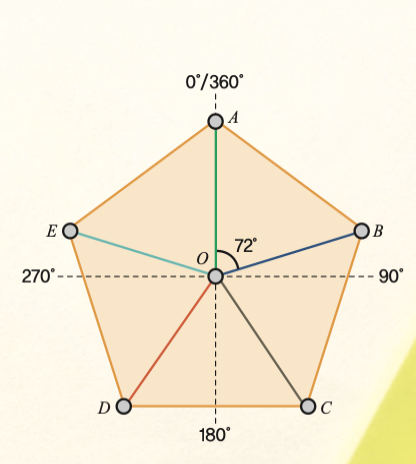
정오각형은 모든 변의 길이와 각의 크기가 같은 오각형으로, 위의 그림과 같이 다섯 개의 합동인 이등변삼각형으로 나눌 수 있다. 이등변삼각형의 꼭지각은 정오각형 중심의 360°를 5등분한 360°÷5=72°다. 5개의 이등변삼각형 중 72°를 이루는 두 변을 잘 골라 그위에 각각 시침과 분침을 놓으면 2시 24분을 나타내는 정확한 시계를 만들 수 있다. 왜 그럴까?

분침은 60분에 360°를 회전한다. 즉, 1분에 6°를 회전한다. 시침은 12시간 동안 360°를 회전하므로, 1시간에 30°, 따라서 1분에 0.5°를 회전한다. 간단하게 계산하기 위해 정각 12시를 알리는 시침과 분침의 위치는 0°고, 시계 방향으로 한 바퀴를 돌면 360°가 된다고 하자. 그러면 n시를 알리는 시계에서 분침은 0°에, 시침은 30°×n에 있다. x분이 흐르면 분침은 6x°에 있고, 시침은 30n° 에 1분에 0.5°를 더 회전하므로 (30n+0.5x)°에 있다.

여기서 시침과 분침이 이루는 각의 크기가 72°가 되는 상황은 2가지로 나눌 수 있다. 분침의 각도에서 시침의 각도를 뺐을 때 72°가 되는 상황, 시침의 각도에서 분침의 각도를 뺐을 때 72°가 되는 상황이다. 이 중 앞의 상황에 대해생각해 보자.

따라서 위의 정오각형에서 OB에 시침을, OC에 분침을 놓으면 정확한 ‘2시 24분’을 가리키는 시계가 된다. 원 모양의 색종이로 정오각형을 접어 이 시계를 만들어 보자.