d라이브러리

매년 12월 31일에서 1월 1일로 넘어가는 시간이 되면 어김없이 들려오는 제야의 종소리! 올해는 코로나19로 인해 67년 만에 처음으로 종을 치지 않는다고 해요. 아쉬운 마음을 담아 보신각 종을 직접 만들어 보겠습니다!

※ 편집자 주
LOL, 오버워치, 배그부터 다양한 인디게임까지 섭렵한 게임 인생 6년차 퓨처킴. 하지만 마인크래프트(이하 마크)는 처음이다. 회사에서 게임하는 게 조금 눈치 보이지만 마크 초고수가 되는 그날까지, 나는 달린다!

댕~댕~. 꼭 웅장한 종소리가 울리는 것만 같아요! 위가 볼록한 게 마치 밥솥을 뒤집어 놓은 것 같은 모양의 종을 보고 있으니 떠오르는 게 있어요. 바로 ‘정규분포’예요.

종 모양의 정규분포란? 

동전 1개를 던져서 나올 수 있는 경우는 앞면과 뒷면 이렇게 2가지예요. 여러 번 던져도 매번 똑같이 2가지 경우만 나오기 때문에 각 면이 나올 확률은 언제나 1/2로 같죠. 그렇다면 동전을 2번 던졌을 때 앞면이 나올 확률은 얼마일까요?　

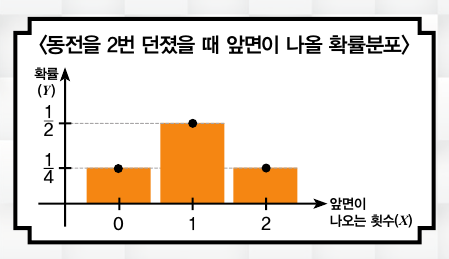
　동전을 2번 던졌을 때 나올 수 있는 경우는 (앞면, 앞면), (앞면, 뒷면), (뒷면, 앞면), (뒷면, 뒷면)으로, 앞면은 0번에서 2번까지 나올 수 있어요. 각 경우가 나올 확률을 구해보면 앞면이 0번 나올 확률은 총 4가지의 경우 중 1가지이므로 1/4이에요. 앞면이 1번 나올 확률은 총 4가지 경우 중 2가지이므로 1/2이죠. 2번 나올 확률 역시 총 4가지 경우 중 1가지이므로 1/4이에요. 

동전을 여러 번 던졌을 때 앞면이 나오는 횟수를 X, 확률을 Y로 두고 그래프를 그리면 이를 ‘확률분포’라고 불러요. 이때의 변수 X를 특별히 ‘확률 변수’라고 합니다.

그리고 동전은 100번, 1000번, 1만 번으로 점점 많이 던질수록 확률분포는 정규분포에 가까워집니다. 정규분포는 확률 변수 X에 대응하는 확률 Y가 평균을 중심으로 좌우가 대칭인 종 모양을 이루는 분포를 말해요.

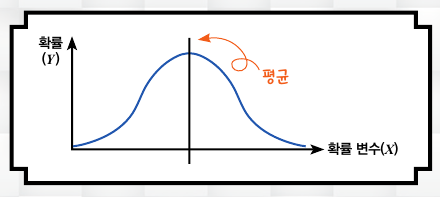
정규분포는 왜 중요할까? 

정규분포는 통계학에서 가장 중요한 분포로 평가되는데요, 그 이유는 자연에서 관찰할 수 있는 많은 현상이 정규분포를 따르기 때문이에요. 

독일 수학자 카를 프리드리히 가우스는 잠깐 나타났다 사라진 소행성 세레스의 움직임을 파악하고자 41일 동안 관측한 22개의 자료로 세레스의 궤도를 추정하는 계산을 했어요. 이때 예측한 값과 실제 값의 차이, 즉 오차를 최소화하고자 노력했는데 그러려면 오차의 분포가 정규분포를 따라야 한다고 판단했어요. 가우스의 이 판단은 지금까지도 옳다고 여겨지며 자연과학뿐 아니라 사회학, 심리학에서도 실험할 때 생기는 오차의 분포를 정규분포로 가정해요. 

 정규분포를 따르는 또 다른 사례도 살펴볼게요. 주위를 보면 성인 남성의 키는 190cm대나 150cm대보다는 170cm대인 경우가 많을 거예요. 성인 여성은 150cm 후반인 경우가 많고요. 그 이유는 우리나라 남녀 평균 키가 각각 170.63cm와 157.11cm이기 때문이죠(국민건강보험공단, 건강검진통계). 우리나라 성인의 키를 남녀로 구분해 그래프를 그리면 이 자료 역시 평균을 중심으로 종 모양을 이루는 정규분포에 가까워요. 

정규분포를 따르지 않는 확률분포도 자료의 개수가 충분히 크면 ‘표준화’라는 작업을 통해 정규분포로 만들 수 있어요. 학교 내신 성적의 등급이나 대학수학능력시험의 등급은 시험을 본 학생들의 원래 점수로 이뤄진 분포를 표준화해 정규분포로 만든 뒤 매긴 거랍니다. 

 1년 추가 연재 기념! 이번에 참여해주시는 분께는 퓨처킴이 준비한 선물을 드립니다. 새해와 관련된 작품을 만들어 보내주세요!