일단 종이접기가 무엇인지 알아보긴 했는데, 종이접기로 수학동아 캐릭터를 접을 수 있는 거야? 종이접기로 원하는 아무거나 접을 수 있냐고~?

단 한 장의 종이로 접는 종이접기를 떠올리면 어떤 작품이 생각나나요? 종이학부터 꽃, 배 같은 우리 주변의 자연과 사물을 접은 모습이 떠오르는데요, 대체 어떤 대상을 종이접기로 만들 수 있을까요? 놀랍게도 모든 물체를 만들 수 있습니다.
2017년 7월 호주에서 열린 ‘계산기하학 심포지엄’에서 미국 매사추세츠공과대학교(MIT)와 일본 도쿄대학교의 공동 연구팀이 컴퓨터에 만들고 싶은 대상 이미지를 입력하면 종이접기로 만들 수 있게 도면을 그려주는 프로그램을 개발해 발표했습니다. 그보다 훨씬 전인 1999년에도 연구팀은 비슷한 프로그램을 선보였습니다. 하지만, 이때는 매우 길쭉한 종이로 접는 것이어서 진정한 종이접기라고 보기 어려웠습니다. 마치 긴 리본을 물체에 두른 것처럼 작품이 만들어졌기 때문에 결과물이 튼튼하지 않았죠.

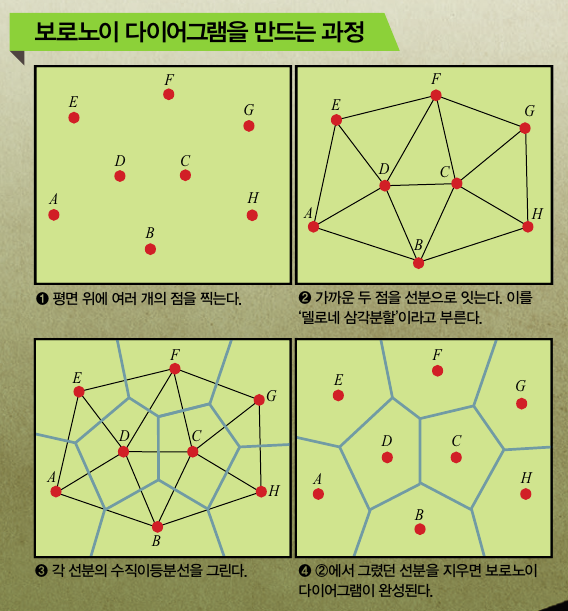
그래서 연구팀은 정사각형에 가까운 종이를 이용해서 더 단단한 구조를 만들 수 있는 종이접기 방법을 고안하고자 했습니다. 먼저 만들고 싶은 3차원 물체의 표면을 삼각형으로 분할했습니다. 물체의 곡선까지 나타낼 수 있을 정도로 작은 삼각형으로 나눈 뒤, 한 장의 종이 위에 이 삼각형들을 적절히 배치했죠. 그리고 종이를 접었을 때 삼각형들이 모여 3차원 물체를 만들 수 있도록 수십, 수백 개의 주름을 삼각형 사이사이에 배치했습니다. 이때 접는 주름은 ‘보로노이 다이어그램’을 이용해 그렸죠.


보로노이 다이어그램은 평면을 수학적으로 나누는 방법입니다. 우선 평면에 고르게 점을 찍고, 그 점 중에서 가장 가까운 점 2개를 모두 연결합니다. 그리고 점을 이은 선들의 수직이등분선을 그어 평면을 나누는 방식이죠. 이 방법을 이용하면 삼각형 사이의 주름을 효율적으로 그릴 수 있습니다. 여기서 수직이등분선이란 주어진 선분을 정확히 2등분하면서, 선분에 수직인 선을 말합니다.