d라이브러리

여러분은 특별히 좋아하는 숫자가 있나요? 행운의 7? 한국인이라면 삼세번의 3? 수학을 좋아하면 누구나 한번쯤 외워보는 원주율? 저도 좋아하는 숫자가 여럿 있지만, 이번엔 그중에서도 군론에서 빼놓을 수 없는 거대한 숫자를 소개하려고 합니다.  

우리 생활에서 흔히 접하는 수는 자연수예요. 이런 자연수 안에도 여러 종류의 수가 있습니다. 짝수, 홀수, 삼각수, 완전수 등이요. 그중에서 가장 중요한 자연수의 모임을 고르라면, 모든 수학자가 아마 ‘소수’라고 외치지 않을까 싶습니다. 1과 자신만을 약수로 갖는 소수는 모든 수를 이루는 기본 구성 요소이기 때문에 수학에서 매우 중요합니다.  

군론의 기본요소, 단순군!

군론에도 소수와 같이 기본요소가 되는 군이 있습니다. 바로 ‘단순군’인데요. 소수가 1과 자신만을 약수로 갖는 수이듯, 단순군 역시 1에 해당하는 ‘자명군’과 자기 자신만을 ‘정규 부분군’으로 갖습니다. 여기서 군이란 주어진 연산에 대해 닫혀 있고, 항등원과 역원이 존재하며, 결합법칙을 만족하는 집합을 말합니다.

이런 단순군이 군론에서 중요하게 된 건 ‘조르당-횔더 정리’ 덕분입니다. 19세기 프랑스 수학자 카미유 조르당과 독일 수학자 오토 횔더는 원소의 개수가 유한개인 모든 ‘유한군’은 단순군으로 분해할 수 있다는 조르당-횔더 정리를 증명했습니다. 수학에 있는 수많은 대칭 구조는 군론을 통해 이해할 수 있는데, 이 정리로 단순군은 군론의 가장 근본적인 구성 요소가 된 겁니다. 

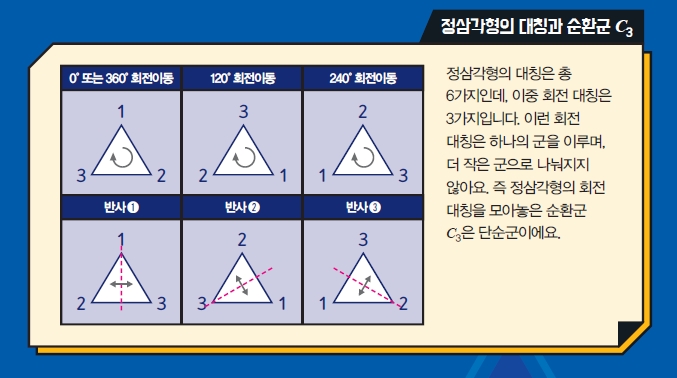
단순군의 가장 쉬운 예로는 소수 p개의 원소를 가진 순환군 Cp가 있습니다. 정p각형의 회전 대칭만을 모아놓은 군이라고 생각하면 쉽습니다. 정삼각형의 회전 대칭은 3개, 정오각형의 회전 대칭은 5개, 정칠각형의 회전 대칭은 7개겠죠? 이들이 모두 단순군입니다.

얼핏 보면 소수 개의 변을 가진 정p각형의 회전 대칭이 단순군인 건 당연해 보입니다. 소수가 1과 자신 외의 다른 수로 나눠지지 않듯이, 소수 개의 원소를 가진 이 군들 역시 더 작은 군들로 나눠지지 않을 테니까요. 하지만 안타깝게도 단순군이라는 이름과 달리 실제 단순군을 예측하는 건 그렇게 단순하지 않습니다. 

대칭 주기율표를 완성하라! 아틀라스

단순군의 중요성이 알려진 뒤 수학자는 자연스럽게 다음 단계로 나아갔습니다. 모든 단순군을 찾아내고 분류하는 일이었죠. ‘유한 단순군 분류 정리(2004)’로 불리는 이 연구는 증명 과정에 기여한 수학자만 100명이 넘고, 논문의 분량이 15,000쪽이 넘는 수학 역사상 전례 없던 가장 거대한 정리가 됩니다. 어떤 유한군이 단순군인지 증명하고, 어떤 성질을 가지는 단순군인지 밝힌 것이죠.

이 정리에는 5차 이상의 방정식은 근의 공식이 없다는 걸 밝히는 데 주요한 역할을 했던 ‘5차 이상의 교대군’과 소수 개의 변을 가진 정다각형의 회전 대칭 군인 순환군 Cp, 비슷한 성질을 가지는 16가지의 리(Lie) 형태의 군, 그 외에 다른 성질을 가지는 26가지의 ‘산재군’이 이름을 올렸습니다. 
분류 정리에 이바지한 수학자를 뽑으라면 많은 사람의 이름이 나오겠지만, 가장 중요한 역할을 한 수학자는 모든 증명을 총괄했던 다니엘 고렌슈타인과 증명을 마무리한 마이클 에셔바허입니다. 

한편 유한 단순군 분류 정리의 끝이 보이지 않던 1970년대 후반 무렵 영국 수학자 존 콘웨이를 필두로 한 수학자들은 유한 단순군을 원소로 생각한 대칭 주기율표 작성에 나섭니다. 바로 ‘아틀라스 프로젝트’입니다. 

유한 단순군 분류 정리에서 가장 어려웠던 것은 26가지의 산재군을 찾는 것이었습니다. 산재군은 다른 군과 성질이 다르고 불규칙해 발견하는 건 물론 원소의 개수가 유한한지 무한한지 알아내는 것도 어려웠거든요. 아틀라스 프로젝트를 시작할 당시 콘웨이를 비롯한 수학자들은 산재군에 대해서 아는 것이 별로 없었습니다.

괴물 같은 정리 속 괴물 같은 군

유한군의 바다에서 ‘보물찾기’를 하는 마음으로 특이한 산재군들을 찾던 콘웨이는 어느 날 어마어마한 크기의 산재군을 예측합니다. 콘웨이의 추측이 맞다면 이 산재군은 무려808,017,424,794,512,875,886,459,904,961,710,757,005,754, 368,000,000,000개의 원소를 갖는 군이었죠. 이렇게 거대한 군이 어떤 분해도 되지 않는 단순군이라니, 처음엔 쉽게 믿을 수 없었지만 그의 추측은 맞았습니다. 미국 수학자 로버트 그리스 주니어와 독일 수학자 베른트 피셔가 이를 증명했거든요. 피셔는 이 거대한 군에 ‘괴물’이라는 이름을 붙였습니다. 

이 괴물군은 26개의 산재군 중 가장 크기가 큰 군으로, 이 군을 관찰할 수 있는 가장 작은 차원은 무려 196,883차원이라고 합니다. 그야말로 괴물이란 이름이 이보다 잘 어울릴 수 없겠죠?

괴물군이 수학사에 중요한 이유는 단순히 거대해서만은 아닙니다. 현대 정수론에서 아주 중요한 모듈러 함수와 깊은 연관이 있다는 것이 밝혀졌기 때문인데요, 이 연구 성과로 영국의 수학자 리처드 보처즈는 1998년에 젊은 수학자가 받을 수 있는 최고의 영예인 필즈상을 받았습니다. 여기서 모듈러 함수란 어떤 정수를 또 다른 정수로 바꿔주는 함수입니다. 

이렇게 거대한 수와 그 속에 숨은 더 거대한 군론을 이야기해봤는데요, 여러분도 각자 기억에 남는 신기한 수나 신기한 정리가 있나요? 이참에 한번 재밌는 수를 찾아보세요!