d라이브러리

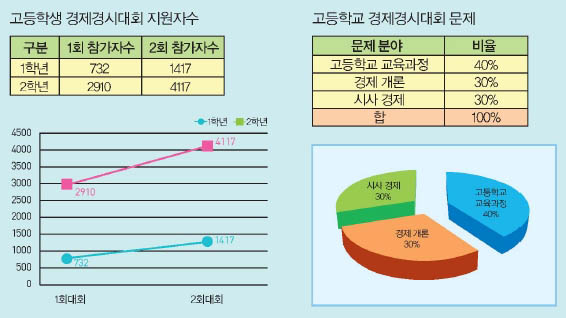
‘클로버 퍼즐’은 위상수학의 한 분야이자 배배 꼬인 매듭을 교차점의 개수에 따라 분류하고 매듭끼리 합성해 그 성질을 파악하는 ‘매듭 이론’과 관련이 깊은 퍼즐입니다. 우리가 흔히 알고 있는 매듭과 수학에서 말하는 매듭은 어떤 차이가 있는지 살펴보고, 클로버 퍼즐의 해법을 분석해보도록 해요!  

※ 편집자 주
KPP(한국 퍼즐 파티)는 ‘퍼즐을 좋아하는 사람들의 모임’입니다. 저희의 퍼즐 이야기를 통해 신기한 퍼즐과 그 속에 숨은 수학을 즐겨보세요!

중국의 퍼즐 디자이너 아론 왕이 고안한 클로버 퍼즐은 세잎클로버 장식이 달린 목걸이에 반지를 걸어놓은 듯한 모습을 하고 있습니다. 정확히 말하면 목걸이 끈을 반지 모양 고리에 통과시킨 뒤 그 고리가 빠지지 않도록 한쪽 끝에 커다란 나무 공을 매달아 놓은 모습이지요. 이 고리를 목걸이로부터 분리하는 게 클로버 퍼즐의 목표입니다.

얼핏 보면 절대 분리할 수 없을 것처럼 보이죠? 하지만 대부분의 퍼즐이 그렇듯 마술 같은 해법이 있습니다. 철사를 엇갈려 만든 세잎클로버를 끈이라고 생각하고 양 끝을 당기면 매듭이 만들어지는데, 이 매듭을 연구하는 매듭 이론이 해법의 핵심입니다.

매듭 하면 우리는 신발 끈을 묶은 것처럼 꼬인 끈을 떠올리는데요, 위상수학의 매듭 이론에서 말하는 매듭은 조금 다릅니다. 아무리 단단하게 묶인 끈도 양 끝이 떨어져 있으면 시간이 걸릴 뿐 언젠가 풀 수 있어 묶이지 않은 끈과 똑같다고 생각합니다. 위상수학에서는 자르거나 구멍을 내지 않고 어떤 물체와 똑같이 만들 수 있으면 두 물체를 같은 것으로 보거든요. 그래서 끈을 아무리 조작해도 풀 수 없도록 양 끝을 이어붙인 끈만을 ‘매듭’이라고 하죠. 이런 매듭의 특징을 살펴보며 클로버 퍼즐의 해법을 찾아봅시다! 

 
세 잎 매듭을 풀려면 매듭을 만들어라!

클로버 퍼즐의 해법이 생각보다 어려우니 단계적으로 생각해볼게요. 우선 나무 공의 지름이 고리의 지름보다 크기 때문에 나무 공 쪽으로 고리를 빼는 건 불가능합니다. 따라서 고리를 세잎클로버 장식의 한쪽부터 통과시켜서 반대쪽 끝으로 빼야합니다. 

이제 고리의 움직임을 방해하는 끈을 어떻게 처리할지 생각해봅시다. 만약 끈을 적절히 움직여 아래 그림①-1처럼 세잎클로버에 딱 붙게 할 수 있다면 아마 고리를 쉽게 분리할 수 있겠죠.

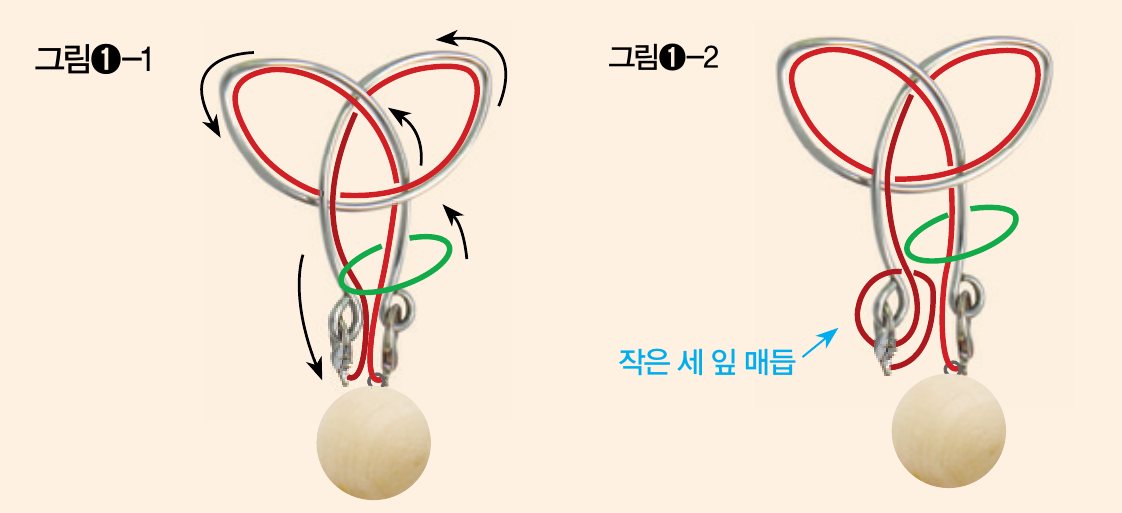
하지만 문제는 끈을 이렇게 만들 수 없다는 겁니다. 그림①-1에서 철사와 끈을 쭉 펴면 오른쪽 그림②처럼 교차점이 없는 ‘영 매듭’이 됩니다. 하지만 클로버 퍼즐은 그림③과 같은 ‘세 잎 매듭’이기 때문에 아무리 변형시켜도 영 매듭으로 만들 수 없죠.

그런데 이 문제는 의외로 쉽게 해결할 수 있습니다. 그림①-2처럼 세잎클로버의 한쪽 끝에 작은 세 잎 매듭이 만들어지도록 하면 철사와 끈이 기존 매듭을 유지하면서도 고리가 통과할 수 있거든요. 그림①-2처럼 만드는 방법은 여러분에게 맡길 테니 도전해보고 궁금한 것이 있으면 폴리매스 홈페이지에서 물어봐 주세요!