d라이브러리

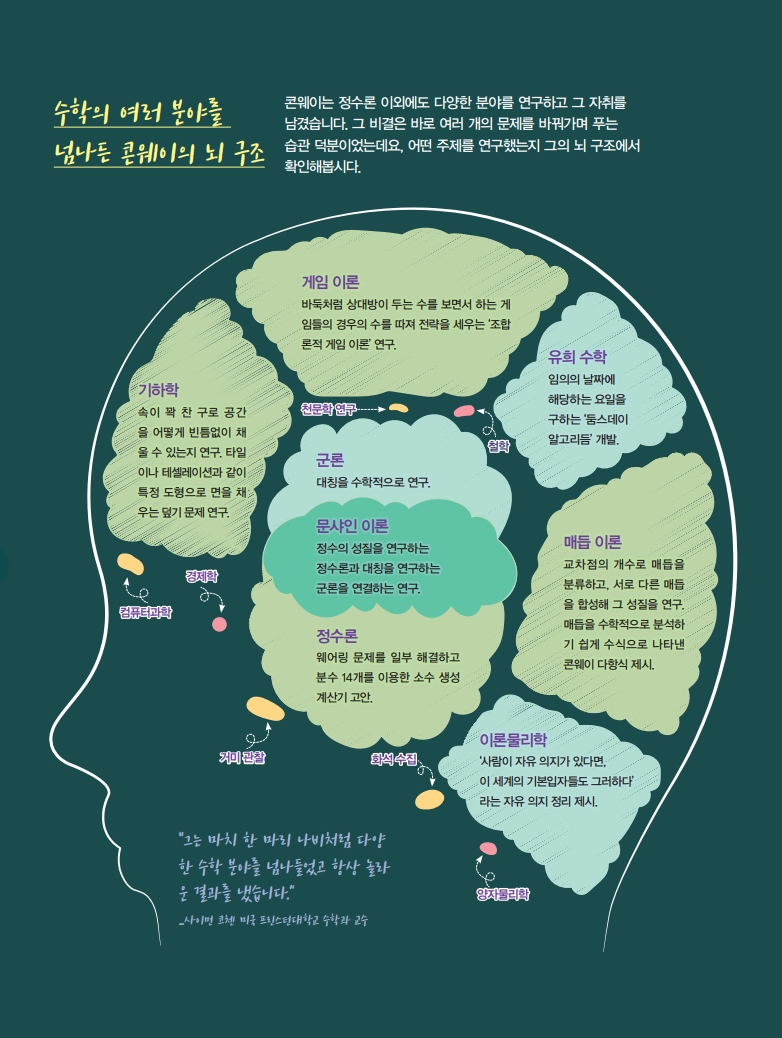
코로나19가 전세계를 한창 할퀴던 4월 11일, 수학계에는 애도의 물결이 일었습니다. 수학의 여러 분야를 넘나들며 놀라운 연구 결과를 발표한 것은 물론, 수학을 대중에게 알리는 데 힘을 쏟았던 영국의 수학자 존 콘웨이의 사망 소식 때문이었습니다. 수학자들이 20세기에 빼놓을 수 없는 수학자로 꼽는 콘웨이의 발자취를 따라가 보겠습니다.

1부 “수학은 재밌어야 한다”

“우리가 학생에게 가르치는 수학은 너무 어렵다. 
이해하기 어려운 이런 바보 같은 수학은 필요 없다.”
살아생전에 이런 말을 한 콘웨이는 누구나 수학을 즐길 수 있는 수학 게임 개발에 앞장섰습니다.

페르마의 마지막 정리를 푼 앤드루 와일스, 게임 이론을 연구해 노벨 경제학상을 받은 존 내시, 다방면에서 활약하는 필즈상 수상자 테렌스 타오까지! 당대 최고의 수학자들이 프린스턴대학교 수학과를 거쳐 갔습니다. 

이곳에서 30년 넘게 교수로 일한 콘웨이는 어려운 수학 연구에만 몰두했을 것 같지만, 실제로는 쉽고 재밌는 수학을 널리 알리기 위해 다양한 활동을 했습니다. 게임이나 퍼즐을 직접 개발해 대중들이 자연스럽게 수학을 접할 수 있도록 힘을 쏟았고, 수학 캠프에서 중·고등학생을 만나 수학의 재미를 알렸습니다.

이런 그를 일컬어 수학을 이용한 놀이와 게임, 퍼즐 등을 개발하고 연구하는 ‘유희 수학자’라고 하는데요, 그를 유명한 유희 수학자의 반열에 올리는 데는 미국의 과학저술가이자 유희 수학자인 마틴 가드너가 크게 기여했습니다. 

둘은 1950년대에 처음 만난 이후로 편지를 주고받으며 유희 수학에 관한 아이디어를 공유했습니다. 가드너는 미국 과학 잡지 ‘사이언티픽 아메리칸’에 수학 칼럼을 연재했는데, 거기에 콘웨이가 고안한 게임을 자주 소개했습니다. 1967년 새싹 게임, 1970년 라이프 게임, 1972년 하켄부시, 1974년 천사와 악마 문제 등이 대표적입니다. 특히 라이프 게임을 다룬 기사는 역대 가장 많은 독자 편지를 받았을 정도로 큰 인기를 누렸습니다.

콘웨이는 가드너를 중심으로 수학, 과학 대중화에 관심이 있는 수학자와 물리학자, 컴퓨터과학자, 철학자, 예술가, 작가 등이 모이는 ‘마틴 가드너의 수학 비밀 정보망’의 일원으로도 열심히 활동했습니다. 

이 모임은 가드너가 세상을 떠난 2010년 이후에는 이름을 ‘마틴 가드너를 위한 모임(G4G)’으로 바꾸고 2년에 한 번씩 모여 유희 수학에 대해 논하는데, 여기서도 콘웨이는 수학의 즐거움을 나누며 마지막까지 유희 수학자로서 활동했습니다.

2부 "수학자의 수학자"

대중들에겐 수학을 쉽고 재밌게 설명한 콘웨이는 수학자들 사이에서는 존경받는 수학자로 꼽힙니다. 수학의 대중화에 힘쓴 것만큼 수학 연구에도 대단한 성과를 냈기 때문이었습니다.

콘웨이가 수학계에 이름을 처음 알린 건 일명 ‘웨어링 문제’라고 불리는 정수론 분야의 난제를 부분 해결한 것입니다. 1770년 영국의 수학자 에드워드 웨어링이 제시한 이 난제는 자연수를 k제곱수의 합으로 표현할 때 필요한 수의 최소 개수 s를 찾는 문제입니다. 예를 들어, 자연수 5는 2²+1², 6은 2²+1²+1²으로 나타낼 수 있습니다. 첫 번째는 k가 2일 때 s가 2이고, 두 번째는 k가 2일 때 s가 3인 경우를 보여주죠.

지금이야 자연수는 모두 제곱수 4개, 세제곱수 9개의 합으로 표현할 수 있고, 19개의 네제곱수의 합 등으로 나타낼 수 있다는 것이 증명돼 알려졌지만, 콘웨이가 연구할 당시에만 해도 다양한 k에 따른 s의 최솟값을 계속 찾아가는 중이었습니다.

콘웨이는 k가 5일 때 s가 37이라는 것을 밝힙니다. 즉 모든 자연수를 다섯제곱수 37개의 합으로 나타낼 수 있다는 겁니다. 이렇게 유명한 난제를 일부 해결해 박사학위를 받음과 동시에 수학계에 이름을 알립니다.

또 콘웨이는 소수를 만들어내는 분수 14개를 정의했습니다. 2를 시작으로 곱했을 때 정수가 되도록 14개의 분수 중 하나를 골라 계속 곱해나가면 2의 거듭제곱 수가 나오는데, 이때 지수에서 소수가 나타납니다.

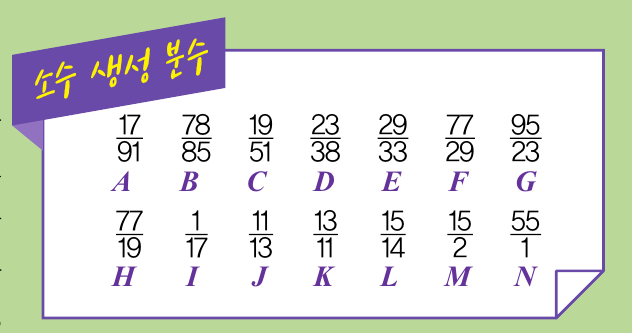
자세히 살펴볼게요. 2에 곱해 그 결과가 정수인 분수는 M(15/2)과 N(55/1)입니다. 둘 중 하나를 골라 계산하면 되는데, 여기서는 순서가 가장 앞인 분수 M을 택해 2에 곱하겠습니다. 그러면 2×M=15가 됩니다. 다음으로 15에 곱해 그 결과가 정수인 분수 N을 찾습니다. 15×N은 825이며, 825에 분수 E(29/33)를 곱하면 725가 됩니다. 이 과정을 반복하면 2의 거듭제곱 수인 4=2²이 나옵니다. 이때 지수인 2가 소수인 것을 알 수 있죠. 

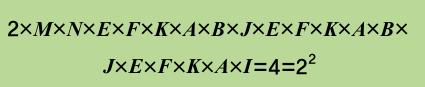
결괏값인 4에서 시작해 50단계를 더 거치면 8=2³이 나와 그다음 소수인 3을 얻을 수 있습니다. 이외에도 콘웨이는 리처드 가이 캐나다 캘거리대학교 수학과 명예교수와 함께 수에 관한 연구들을 정리해 ‘수의 바이블’이라는 책을 내기도 했습니다. ‘수’라는 개념이 발달하는 과정부터 다양한 수의 성질을 한눈에 보기 쉽게 기하학적으로 설명해 ‘수의 백과사전’으로 통하고 있습니다.

학교에 있을 때 콘웨이는 늘 밧줄이나 동전, 카드, 주사위 등을 주머니에 넣고 다녔습니다. 만나는 사람들에게 유희 수학을 선보이며 자연스럽게 관련된 수학에 흥미를 갖도록 하기 위해서였지요. 그리고 연구실보다는 주로 건물 중간의 소파에 앉아 칠판이나 종이, 펜을 써서 학생들과 수학 이야기를 나눴습니다.

그는 비록 코로나19로 안타깝게 세상을 떠났지만, 많은 사람과 수학의 재미를 나누고 싶었던 그 마음은 영원히 남아있을 겁니다.