d라이브러리

피터 테이트 & 조지 데이비드 버코프

의미 없는 ‘개념’은 없다

처음 소개할 신스틸러는 4색정리에 도전했다가 의외의 곳에서 쓰이는 수학 이론을 만든 수학자입니다. 주인공은 바로 스코틀랜드 수학자 피터 테이트와 미국 수학자 조지 데이비드 버코프입니다.
1880년 테이트는 4색정리를 증명하기 위해 문제를 다른 문제로 바꿨습니다. 다리가 없고 모든 점의 차수가 3이며 인접하는 변이 다른 색이 되도록 3가지 색으로 모든 변을 칠할 수 있는 그래프 ‘스나크’를 정의한 뒤, 모든 스나크는 평면 그래프가 아니라는 사실을 증명하는 게 4색정리를 푸는 것과 같다는 걸 밝힌 거죠. 여기서 ‘다리’는 그래프를 이루는 한 변을 없앴을 때 그래프를 2개로 나누는 변이고, ‘차수’는 한 꼭짓점에 연결된 변의 수를 말합니다. 또 평면 그래프는 변들이 꼭짓점 외에는 만나지 않게 평면에 그릴 수 있는 그래프죠.

한편 버코프는 1900년대 초 4색정리를 ‘n색 문제’로 확장해 색이 n개일 때 모든 평면 지도를 칠하는 방법이 1개 이상 있음을 증명하려고 했습니다. n색 문제를 증명하면 n=4인 경우인 4색정리는 저절로 풀리거든요.

결론부터 말하면 두 수학자는 증명에 ‘실패’했습니다. 심지어 4색정리의 증명 과정에서 두 사람의 아이디어가 쓰이지도 않았죠. 

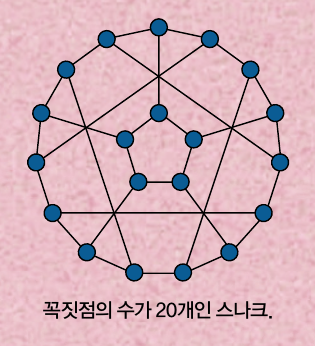
그런데 신스틸러인 이유는 두 수학자가 만든 개념이 현재 그래프 이론과 관련된 여러 수학 문제를 풀 때 유용하게 쓰이기 때문이에요. 현재 수학자들은 꼭짓점의 수를 늘려가며 다양한 모양의 스나크를 찾고, 스나크와 관련된 여러 연구를 하고 있습니다. 

버코프가 문제를 확장해 푸는 과정에서 정의한 함수 P(n)은 어떤 그래프에서 이웃한 꼭짓점을 서로 다른 색으로 칠할 때 n개 이하의 색만 써서 칠하는 방법의 수를 나타내는데, 이 함수는 현재 ‘채색 다항식’이라고 불리며 그래프를 연구하는 데 중요한 도구로 쓰이고 그 자체로도 흥미로운 연구 대상입니다.

피터 테이트

매듭은 거들 뿐!

말이 나온 김에 테이트가 신스틸러로 활약한 사례를 한 가지 더 들어보겠습니다.

1850년대 물리학자들은 물질이 ‘원자’로 이뤄져 있다는 사실을 깨닫고, 원자의 구조를 설명할 수 있는 모형 개발에 열을 올리고 있었습니다. 이에 영국의 물리학자 윌리엄 톰슨은 1867년 원자가 소용돌이로 이뤄졌다는 흥미로운 모형을 발표했죠.

톰슨이 발표한 원자 모형에 영감을 준 사람은 독일의 물리학자 헤르만 폰 헬름홀츠였는데요, 헬름홀츠는 유체의 모든 운동은 작은 소용돌이들의 상호작용으로 만들어지기 때문에 소용돌이의 성질을 분석하면 유체의 운동도 예측할 수 있다고 생각했죠. 이런 생각을 토대로 소용돌이에 관한 몇 가지 논문을 발표했습니다. 이 연구에 영감을 받은 톰슨이 원자가 특정한 모양과 고리의 수를 지닌 소용돌이로 이뤄졌다는 ‘소용돌이 원자 이론’을 완성한 겁니다.

한편 톰슨의 오랜 친구였던 테이트는 소용돌이 모형에 푹 빠져 이를 뒷받침하는 이론을 만듭니다. 원자를 이루는 소용돌이의 모양에 따라 원자의 성질이 결정된다면 소용돌이가 얽힌 모양, 즉 매듭을 종류별로 분류하면 원자를 분류할 수 있다고 생각했죠. 이 아이디어가 ‘매듭 이론’을 만든 겁니다. 테이트는 교차하는 횟수에 따라 매듭을 분류해 1885년 교차점이 10개 이하인 모든 매듭을 발표했습니다. 

1890년대에 이르러 전자가 발견되면서 소용돌이 모형은 점차 잊혀졌습니다. 하지만 매듭 이론은 발전을 거듭한 끝에 공간을 수학적으로 분류하거나 DNA 구조를 설명할 때는 물론 입자를 진동하는 끈으로 설명하는 ‘초끈이론’ 연구에도 응용됩니다. 이쯤 되면 신스틸러가 아니라 주인공이라고 해도 손색없겠죠?

에드바르 프레그먼

수학 돌다리도 두드려야 제 맛! 

마지막 신스틸러를 만나기 위해 프랑스 수학자 앙리 푸앵카레가 다체 문제를 연구하던 19세기로 가보겠습니다. 푸앵카레는 위상수학, 대수기하학, 동역학계 등 현대 수학 전반에 영향을 끼쳤을 뿐 아니라 상대성이론, 열역학, 천체물리학까지 섭렵해 ‘올타임 넘버원’으로 불리는 수학자입니다.

푸앵카레의 대표 업적 중에는 미국 클레이수학연구소에서 100만 달러(약 12억 3000만 원) 상금을 내건 밀레니엄 문제 중 하나인 ‘푸앵카레 추측’을 제시한 것 외에 다체 문제에서 n이 3인 ‘삼체 문제’는 정확한 해를 구할 수 없다는 사실을 증명한 것도 있습니다. 그런데 푸앵카레가 삼체 문제를 푸는 데 결정적인 역할을 한 신스틸러가 있습니다.

1880년대는 힘과 물체의 운동 사이의 관계를 수학적으로 기술하는 ‘고전 역학’이 한창 발전하던 시기입니다. 다체 문제는 태양계 행성들이 특정한 궤도를 따라 운동하는지, 아니면 궤도가 계속해서 변하는지 밝힐 수 있는 중요한 문제였습니다. 하지만 그때까지 n이 3 이상인 경우를 아무도 풀지 못했죠.

때마침 스웨덴 수학자 예스타 미타그레플레르는 스웨덴 국왕의 60세 생일을 기념해 전세계 수학자들을 대상으로 다체 문제처럼 매우 중요한 미해결 문제 4개를 푸는 대회를 열었습니다. 가장 좋은 답을 제출한 수학자에게 상금을 주고 수학 학술지 ‘수학 동향’에 실어 주겠다는 조건을 걸었죠. 물론 수학자들의 관심은 단연 다체 문제로 쏠렸습니다.

이미 천재로 정평이 난 푸앵카레는 참신한 아이디어가 담긴 300쪽짜리 풀이와 함께 풀이 검토를 맡은 심사위원에게 아이디어를 설명한 100쪽 분량의 설명집을 제출했습니다. 푸앵카레의 풀이를 검토한 미타그레플레르는 이내 ‘푸앵카레가 우승했다’고 발표했고, 이제 남은 일은 푸앵카레의 풀이가 담긴 학술지와 설명집을 출판하는 것뿐이었습니다. 미타그레플레르는 자신의 제자이자 편집자로 일하는 에드바르 프레그먼에게 푸앵카레의 풀이를 넘기며 편집을 맡겼죠.

학술지의 책임자 미타그레플레르가 대회를 통해 수학적으로 검증했으니 풀이를 보기 좋게 정리하면 충분했지만, 프레그먼은 그러지 않았습니다. 푸앵카레의 풀이를 처음부터 끝까지 읽으며 본인이 이해하지 못한 부분을 푸앵카레에게 묻고 또 물었죠. 이미 우승이 확정됐는데 계속 질문하니 푸앵카레도 무척 귀찮았겠죠? 그런데 푸앵카레는 프레그먼의 질문에 답하는 과정에서 중대한 오류를 발견합니다. 이 오류를 바로 잡았더니 세 물체가 일정한 궤도가 아닌 무작위로 운동했습니다. 결과가 완전히 뒤바뀌어 버린 거죠.

프레그먼의 꼼꼼함이 없었다면, 잘못된 풀이가 전세계에 퍼지고 우주선의 궤도를 잘못 계산했을지도 모릅니다. 프레그먼이 더욱 돋보이는 이유는 푸앵카레가 풀이를 수정하는 과정에서 동역학계, 카오스 이론 같은 새 연구 분야의 토대를 세웠기 때문이에요!