d라이브러리

삼각형, 사각형 등의 도형들로 평면을 빈틈없이 채우는 테셀레이션(쪽매맞춤)은 동서양을 불문하고 보도블록, 목욕탕 타일, 예술작품, 카펫 등에서 쉽게 찾아볼 수 있습니다. 테셀레이션을 탐구하고 멋진 작품을 만들어 봅시다.

정다각형으로 만드는 테셀레이션

여러 개의 도형을 겹치지 않고 평면이나 공간을 빈틈없이 채우는 것을 ‘테셀레이션’이라고 합니다. 우리말로는 ‘쪽매맞춤’ 혹은 ‘쪽매붙임’, ‘평면 채우기’ 등으로 불리죠. 특히 한 가지의 정다각형으로 만든 테셀레이션을 ‘정테셀레이션’이라고 하고, 정삼각형, 정사각형, 정육각형으로 할 수 있지요. 두 가지 이상의 정다각형을 활용하는 ‘준정테셀레이션’과 ‘반정테셀레이션’도 있습니다. 한 가지 배열을 가지면 준정테셀레이션, 두 가지 이상의 배열이 나타나면 반정테셀레이션이라고
합니다.

물론 정다각형이 아닌 모양으로도 테셀레이션 할 수 있습니다. 또 도형을 거울에 비춘 듯 반사시키고 평행이동하는 ‘미끄럼 반사’ 대칭을 한 뒤 테셀레이션 할 수도 있습니다. 이것을 미술 작품으로 이끈 대표적인 작가가 20세기 초에 활동한 네덜란드 출신의 판화가 마우리츠 코르넬리스 에셔입니다. 이런 다양한 테셀레이션을 만들기 위해서는 먼저 여러 개의 도형이 모여서 360°
를 이룰 수 있는지 알아봐야 합니다.

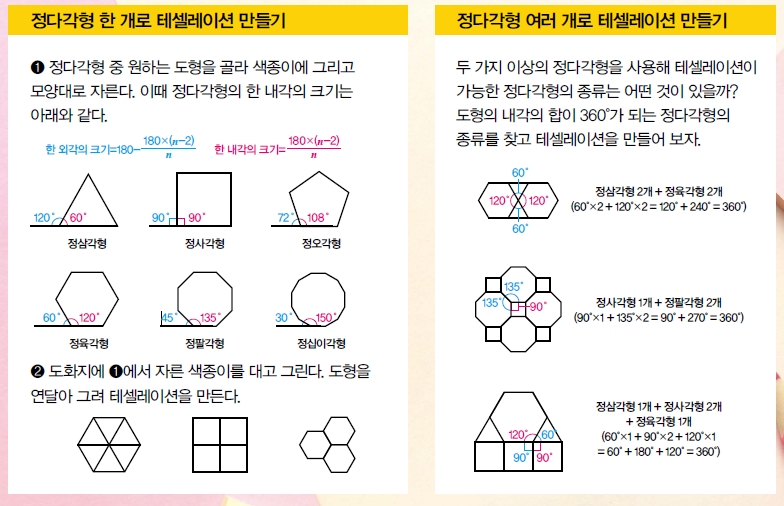
테셀레이션 속 수학 원리

1. 다음 표를 채우고 정삼각형, 정사각형, 정육각형으로 정테셀레이션을 만들 수 있는 이유를 생각해봅시다.

2. 정오각형으로 테셀레이션을 만들 수 없는 이유를 생각해봅시다.

3. 두 가지 이상의 정다각형을 사용하며, 모든 꼭짓점에서 한 가지 배열을 갖는
준정테셀레이션에는 몇 가지 종류가 있는지 알아봅시다.

필자소개

서미나 선생님은 토의와 탐구를 통해 학생들이 수학적 원리를 찾고 발견할 수 있도록 수업하는 방법을 고민하고 이를 실천하는 수학교사입니다. 모둠원끼리 협업을 하며 논리성과 창의성을 키우고, ‘배움-앎-성장’으로 이어지는 수학 수업 디자인에 힘쓰고 있습니다. 또 지역 문화와 명소를
이용한 ‘Math-Tour’ 개발에도 참여하고 있습니다.

※ 수학체험실은 전국수학문화연구회와 함께 합니다.