d라이브러리

렛잇고~ 렛잇고~♬ 안녕, 난 올라프야. 겨울왕국 1편을 본 친구들은 알겠지만, 난 엘사가 ‘Let It Go’ 노래를 부를 때 만들어진 눈사람이야. 1편 이후 뮤지컬, 아이스쇼 등에서 다양한 활동을 하다 드디어 겨울왕국 2편과 함께 영화관으로 돌아왔어. 근데 그거 알아? 애니메이션 겨울왕국을 만든 사람 중에 수학자가 있다는 사실을 말이야.

겨울왕국 1편에서는 자신의 능력을 깨닫고 힘들어하던 엘사가 안나와 함께 두려움을 이겨내는 이야기를 다뤘어. 그런데 궁금하지 않아? 엘사의 놀라운 능력은 어디서 왔을지 말이야. 엘사 역시 마법의 힘에 대해 궁금해하던 순간, 알 수 없는 목소리를 들었어. 그리고 동시에 아렌델 왕국이 위험에 처하지. 의문의 목소리로 평화로운 일상이 흔들리기 시작한 엘사는 안나, 크리스토프, 스벤 그리고 나와 함께 모험을 떠나기로 해. 아렌델 왕국을 떠난 부모님이 왜 영영 못 돌아오게 된 건지 그 이유를 찾고 싶기도 했고 말이야. 그렇게 모험을 시작했어. 

왕국을 다시 평화롭게 만들고 엘사의 힘이 어디서 시작했는지 찾기 위해서 우리는 가장 먼저 트롤들을 찾아갔어. 트롤들은 모든 것을 알고 있으니까. 그런데 트롤 할아버지 파비가 이 일은 과거에서 시작됐다며 엘사의 힘의 비밀과 진실을 찾으려면 북쪽의 마법에 걸린 나라를 지나 미지의 세계로 떠나야 한다고 조언했어. 또 엘사를 부르는 목소리의 주인이 해답을 알고 있을 거라고 했지. 그렇게 멀리 떠난 우리는 거대한 안개에 휩싸였던 마법의 땅을 찾게 돼. 

하지만 “어딜 가든 정령이 나타날 거예요”라는 파비의 마지막 말처럼 순탄치 않을 앞날이 기다리고 있었어. 또 엘사 스스로 자신의 능력이 모험을 하는 데 충분하다고 믿어야 하는데 그게 쉽지 않았지.

과연 우리가 아렌델 왕국을 구할 수 있을까? 그 답을 영화관에서 확인해줘! 그 전에 꼭 알아야 할 게 있어. 아는 만큼 보인다고, 이걸 알면 겨울왕국 2편이 더 재밌을 거야.

겨울왕국을 본 친구라면 누구나 내 귀여운 외모와 엉뚱한 매력에 빠졌을 거야. 어떤 상황에서도 웃음을 잃지 않고 여유를 즐기는 모습이나 통통 튀는 입담도 매력이지만, 그중에서도 빼놓을 수 없는 건 진짜 눈사람 같은 내 모습이지.

진짜 같은 눈을 만드는 알고리듬

겨울에 내리는 ‘눈’을 떠올리면 어떤 모습이 그려져? 하늘에서 펑펑 쏟아져 내리는 함박눈부터 가루처럼 흩날리는 싸라기눈, 눈싸움하기 좋은 잘 뭉쳐지는 눈이 생각나지? 애니메이션의 제목이 ‘겨울’왕국인 만큼 다양한 눈을 잘 묘사해야 해. 

그래서 조셉 테란 미국 캘리포니아대학교 로스앤젤레스캠퍼스(UCLA) 교수팀에게 눈을 묘사하기 위한 알고리듬을 만들어 달라고 부탁했어. 고체지만 쉽게 부서지고, 물처럼 모양을 바꾸기 쉽다는 특징이 있어 기존의 방법으로는 만들기 어려웠거든. 그래서 연속적으로 변하는 대상을 시뮬레이션할 때 많이 쓰는 ‘MPM(Material point method)’ 방법을 새롭게 적용했어. 우리말로 ‘물질 점 방법’이라고 하는데, 당시 이 방법으로 눈을 표현한 게 처음이라 컴퓨터 그래픽스 분야 사람들이 깜짝 놀랐지.

MPM 방법이 뭔지 잠깐 살펴볼까? 먼저 눈은 수많은 눈 결정 입자들로 이뤄져 있어. 움직임을 나타내고 싶은 수많은 눈 입자를 일정한 간격으로 나뉜 격자에 그리지. 여기서 눈 입자를 ‘물질 점’이라고 해. 물질 점들은 가까운 교점으로 묶어서 하나로 생각해. 눈을 원하는 모양으로 바꾸고 싶다면 물질 점과 가까운 격자의 교점에서 속도와 부피, 무게 등의 변화량을 계산하고 다시 물질 점에 반영하는 과정을 통해 눈의 모습을 만들어내지. 이때 처음 물질 점들이 교점에 얼마나 가까운지에 따라 바뀐 정보를 반영하는 정도는 달라져. 

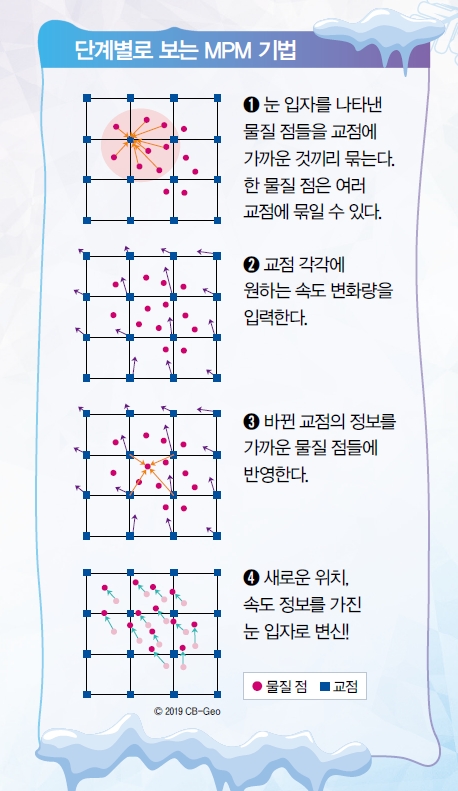
이런 MPM 방법은 오일러와 라그랑지안 방법을 합친 거야. 격자에 있는 눈 입자들을 생각해봐. 라그랑지안 방법은 눈 입자 하나하나에 초점을 맞춰 입자의 성질을 나타내는 거야. 반면 오일러 방법은 입자 대신 격자 같은 고정된 좌표에 집중해. 

MPM 방법에서 처음에는 라그랑지안 방법으로 눈 입자를 나타내. 그러다 교점을 중심으로 눈 입자를 묶으면 라그랑지안에서 오일러 방법으로 바뀌어. 오일러 방법으로 계속 눈 입자의 운동을 계산하다 마지막에 다시 라그랑지안 방법으로 돌아오지. 이 방식을 이용하면 라그랑지안과 오일러 두 방법의 장점을 모두 쓸 수 있어서 더 효과적으로 눈 효과를 만들 수 있어. 

이 방법을 이용하면 입자 하나하나를 매번 그릴 필요 없이 눈의 움직임을 자유자재로 바꿀 수 있지. 그래서 한층 풍성하고 아름다운 엘사의 눈 마법을 표현할 수 있었던 거야.

겨울왕국 2 예고편에서 가장 화제가 됐던 장면은 엘사가 마법을 이용해 파도치는 바다를 얼리며 바다 위를 달려가는 장면이야. 이 예고편은 24시간 동안 1억 1640만 회의 조회수를 기록하면서 역대 가장 높은 애니메이션 예고편의 조회수를 기록하기도 했지.

이 장면은 어떻게 만들었을까? 물과 같은 액체는 형태를 쉽게 바꿀 수 있어. 이렇게 흐르는 성질을 가진 액체나 기체를 ‘유체’라고 하는데, 유체의 운동은 ‘나비에-스토크스 방정식’을 이용해 나타낼 수 있지. 뉴턴의 운동 제2법칙(F=ma)을 유체의 움직임을 나타낼 수 있도록 쪼개서 나타낸 미분방정식으로, 아직 유일한 해가 있는지 조차 몰라. 방정식의 성질도 미지수로 남아있고, 100만 달러 상금도 걸려 있지.

현재 학자들은 이 미분방정식의 해를 근사적으로 찾는 방법을 사용해. 근삿값으로도 물을 표현할 수 있거든. 앞에서 겨울왕국 1편의 눈을 만든 수학자 테란 교수는 디즈니의 또 다른 애니메이션 ‘모아나’ 제작에 참여하며 실제보다 더 생생한 파도를 만드는 ‘APIC 알고리듬’을 개발했어. 나비에-스토크스 방정식의 근삿값을 찾아 역동적인 파도를 나타낼 수 있게 한 거야. 기존에 쓰던 알고리듬은 물방울의 속력을 높이는 데 한계가 있었는데, 새 알고리듬으로 물방울을 격자로 옮겨 더 자연스러운 파도를 만들어낸 거지.

불과 바람의 표현은 ‘등위집합’으로

우리는 물, 불, 바람, 땅의 정령을 만나 위기에 빠져. 이 장면 역시 수학의 힘으로 만들어졌어. 강한 눈보라부터 낙엽이 흩날리는 산뜻한 바람, 그리고 모두 태울 듯한 불까지! 겉으로는 무작위해 보이는 움직임을 나타내기 위해서는 ‘등위집합’을 알아야 해. 등위집합은 유체의 움직임을 수학적으로 기술하는 방법의 하나야. 

바람이나 불의 모양을 한번 생각해봐. 수많은 곡선으로 이뤄져 있지? 이 곡선들은 모여서 곡면을 만드는데, 곡면을 나타내기 위해서는 그 위의 점들을 일일이 추적하는 방법이 있어. 하지만 이 방법을 사용하면 매우 오랜 시간이 걸려. 그래서 생각해 낸 것이 나타내고 싶은 곡면의 점들을 묶어서 함수로 나타내는 등위집합이야. 곡면을 시간에 따라 변하는 함수로 나타내 그 함수를 추적하는 방법이지. 점들을 모두 찍을 필요 없이 함수만 정의하면 돼서 코드로 표현하기도 쉽고, 빠르게 계산 결과를 얻어낼 수 있다는 장점이 있어. 그리고 함수를 조금씩 변형하면 곡면이 두 개로 갈라지거나, 합쳐지는 등 모양이 바뀌는 것도 쉽게 구현할 수 있지. 

덕분에 더 자연스럽고 현실감 있는 장면을 빠르게 만들어 낼 수 있었어. 겨울왕국을 만든 디즈니는 물론 애니메이션을 제작하는 드림웍스, 픽사 등에서도 등위집합을 사용했어. 또 아이디어를 처음으로 제시한 스탠리 오셔 UCLA 교수는 공로를 인정받아 2014 세계수학자대회에서 가우스상을 받았지.

이번에도 ‘렛잇고~♬’에 버금가는 겨울왕국 신드롬을 만들 수 있을까? 제발 흥행해서 다시 바빠졌으면 좋겠어. 나를 만든 제작진들은 1편과 2편이 합쳐져 하나의 이야기를 완성할 거라고 했으니 모두 보라고! 엘사가 부리는 마법의 시작은 무엇인지, 과거 부모님에게 무슨 일이 있었는지 영화관에서 확인하고 곳곳에 숨은 수학도 찾아봐! 1