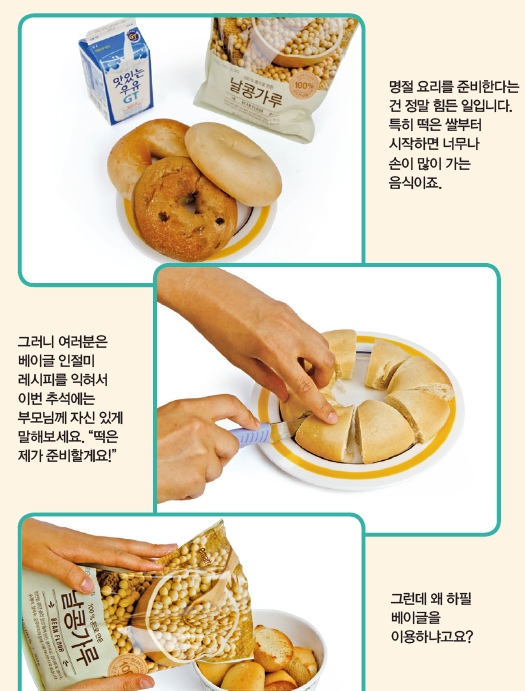
더도 덜도 말고 한가위만 같아라~. 풍성한 한가위가 다가왔습니다. 추석에 먹는 음식이라고 하면 송편이 가장 먼저 떠오르죠? 하지만 늘 먹는 송편은 어딘가 진부하니 저는 특별히 추석맞이 인절미를 만들어보겠습니다. 재료는 한층 더 독특하게 베이글입니다!
위상수학이 무엇인지, 그리고 베이글이 무슨 관계가 있는지 설명하기 전에 먼저 재미있는 퀴즈를 내보겠습니다. 답을 맞혀보고 왜 그런지 이유도 생각해보세요.
초유의 빨대 구멍 개수 논란
‘빨대의 구멍은 1개인가 2개인가?’
이것은 전세계의 네티즌을 떠들썩하게 만들었던 질문입니다. 빨대 구멍 개수를 묻는 이 질문은 우리나라뿐만 아니라 해외 여러나라 게시판을 뜨겁게 달구며 논쟁을 일으켰죠. 여러 달 동안 갑론을박이 이어졌고, 결국 케빈 너드슨 미국 플로리다대학교 수학과 교수가 경제 전문지 ‘포브스’에 기고문을 내고나서야 논란은 종식되었답니다. 너드슨 교수는 뭐라고 답을 내놓았을까요? 또 여러분은 빨대의 구멍이 몇 개라고 생각하시나요?
우선 정답을 발표하기 전에 1개파와 2개파의 주장을 확인해보죠.
2개파 : “위가 뚫려 있고 밑이 하나 더 뚫려있지 않느냐, 딱 보면 답이 보이는데 어떻게 1개냐!”
“건물 앞뒤에 문이 1개씩 있으면 출입구가 2개라고 하지 1개라고 안 한다.”
1개파 : “빨대 구멍은 긴 1개의 구멍이다.”
“빨대 구멍이 2개면 도넛 구멍도 2개냐?”
어때요, 양쪽 의견이 다 그럴듯하죠? 그럼 이제 정답을 발표하겠습니다. 수학적으로 빨대의 구멍은 ‘1개’입니다.
자, 그럼 왜 1개인지 설명하기 위해 빨대를 정의하는 것부터 시작해보겠습니다. 수학에서 빨대는 ‘원과 구간으로 이뤄진 물체’라고 정의할 수 있습니다. 이때 구간이란 빨대 길이만큼의 공간을 나타내는 개념입니다. 그림으로 보면 아래와 같죠.

너드슨 교수는 이처럼 어떤 원을 S¹이라고 할 때 빨대 길이 L에 대해 구간 [0, L]을 I로 표현하고 빨대를 S¹×I라는 식으로 나타냈습니다. 즉 S¹이라는 원을 0부터 L까지 I만큼의 구간으로 늘린 도형이 빨대라는 것이지요. 이 방식을 따르면 구부러진 빨대든 중간이 빙글빙글 꼬인 빨대든 모두 똑같이 S¹×I로 나타낼 수 있습니다. 제아무리 현란하게 생긴 빨대도 원과 구간으로 이뤄져 있다면 위상수학에서는 모두 같은 물체라는 뜻이지요.
물체의 기하학적 성질 고려하는 위상수학
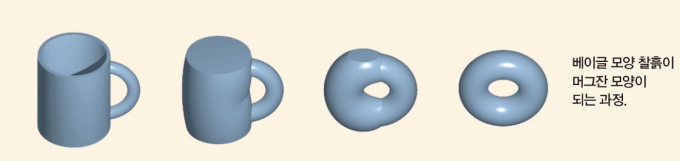
위상수학은 물체의 모양이 바뀌어도 바뀌지 않는 기하학적 성질을 연구하는 분야입니다. 그래서 구멍을 뚫거나 찢지만 않으면 아무리 모양을 바꿔도 수학적으로 같다고 정의합니다. 쉽게 드는 예로 위상수학에서는 베이글 같은 도넛 모양 물체와 손잡이 달린 머그잔이 똑같다고 생각하죠. 아무리 생각해도 베이글이 머그잔과 왜 같은지 모르겠다고요? 그건 우리가 일반적으로 베이글과 머그잔을 구성하는 재료의 성질을 고려하기 때문입니다.
물체의 기하학적 성질만 고려하는 위상수학에서는 머그잔의 딱딱함이나 베이글의 물렁함은 전혀 중요한 사항이 아닙니다. 위상수학에서의 물체는 매우 잘 늘어나는 찰흙으로 이뤄져 있다고 생각합니다. 중간에 구멍을 1개 낸 베이글 모양 찰흙이 있다고 상상해봅시다. 그러면 찰흙을 뜯거나 새로 연결하지 않고 그대로 잘 주물러서 펼치거나 모양을 다듬어 머그잔 모양으로 만드는 건 충분히 가능한 일이겠죠? 이럴 때 위상수학에서는 베이글과 머그잔이 ‘위상 동형’이라고 표현합니다.
그럼 베이글처럼 구멍이 1개인 빨대는 어떨까요? 빨대도 베이글과 위상 동형일까요?
평면상의 어떤 원을 S¹이라고 할 때, 베이글은 S¹×D라고 나타낼 수 있습니다. D는 ‘디스크’를 뜻합니다. 디스크는 구간을 동그랗게 변형시켜 끝과 끝을 맞대면 생기는 도형이죠. 다시 말해 베이글을 잘 펴고 모양을 바꾸면 빨대와 똑같이 만들 수 있습니다. 즉 이 둘은 위상 동형이고, 그러면 기하학적 성질도 같으므로 구멍이 1개인 베이글처럼 빨대도 구멍이 1개인 것이지요. 결론에 도달했군요!
‘구멍’ 들여다보기
하지만 여전히 이렇게 생각하는 분이 있는 것 같네요. “좋아. 위상수학에서 빨대 구멍이 1개라는 건 인정할게. 하지만 대체 그 위상수학에서의 ‘구멍’이란 게 뭐란 말이야?” 좋은 질문입니다. 그럼 여기 자르지 않은 베이글을 들고 구멍을 좀 더 깊이 들여다볼까요?

우리가 일반적으로 ‘구멍’이라고 생각하는 것을 떠올려보죠. 위 그림처럼 얇은 종이에 원을 그리고 그 모양대로 가운데를 잘라냈다고 합시다. 이때 ‘구멍’은 1차원의 선으로 둘러싸인 2차원의 대상이라고 정의할 수 있습니다. 즉 구멍의 수는 ‘폐곡선으로 둘러싸인 공간의 수’로 볼 수 있죠. 구간에는 이런 공간이 있을 수 없으므로 원과 같은 닫혀있는 곡선으로 이뤄진 공간의 수가 구간의 모습과 상관없이 구멍의 수를 결정하는 겁니다. 구간이 빨대처럼 쭉 뻗은 모양이든 베이글처럼 디스크 형태로 말린 모양이든 닫힌 곡선이 1개이므로 구멍이 1개인 것이지요. 어때요, 이제 확실히 이해됐나요?
직관적으로 설명하기 위해 베이글과 빨대 같은 도형을 사용했기에 위상수학이 기하학에만 관련이 있다고 생각할 수 있지만, 사실 위상수학은 오늘날 여러 수학 연구의 기반이 되는 기본 논리에 영향을 주는 분야입니다.
위상수학은 겉모습이 아니라 본질에 집중하는 분야고 이는 문제를 해결하는 접근법으로 활용되기 때문입니다. 수학만이 아니에요. 물리학 문제를 풀 때도 쓰이고 산업 현장에서 회로를 짤 때도 쓰이며, 복잡한 지하철 노선도를 간단하게 만드는 등 실생활에서도 위상수학적 사고는 널리 활용되지요.
당장 너무 어려운 개념부터 알 수는 없으니 이번 방학에는 위상수학적 사고의 바탕이 되는 ‘집합’부터 확실히 익히는 걸 목표로 삼아보세요.