d라이브러리

학생들과 수학 이야기를 나누던 오일러 앞에 맞수가 나타났다. 바로 조선의 수학자 최석정! 누가 진정한 마방진의 고수인지 가리기 위한 대결을 하러 왔단다. 뜬금없이 펼쳐지는 두 수학자의 대결, 과연 최종 승자는 누구일까? 

마방진을 푸는 한 방법인 ‘직교라틴방진’을 연구한 두 수학자 최석정과 오일러의 대결이 시작됐다! 마방진 고수를 가리기 위한 대결은 오각형 마방진 문제인 오일러 프로젝트 68번으로 치르기로 했다. 

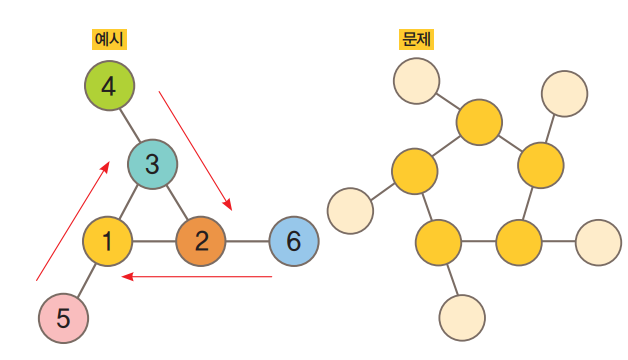
68번 문제는 예시인 삼각형 마방진처럼 오각형 모양의 마방진에 선으로 연결된 세 수의 합이 모두 같게 1부터 10까지의 수를 채우는 것이다. 다만 이럴 경우 답이 여러 개이기 때문에 답안 중 앞으로 소개할 규칙에 따라 수를 모두 이어붙였을 때 가장 큰 16자릿수를 찾는 게 문제다. 예시인 삼각형 마방진은 총 8가지의 답이 가능하다. 같은 선에 있는 수를 화살표 방향에 따라 순서쌍으로 나타낸 뒤, 순서쌍의 첫 번째 수가 가장 작은 순서쌍부터 시계방향 순으로 나열하면 아래 표와 같다. 예를 들어 예시 속 삼각형 마방진 답을 순서쌍으로 나타내면 (4, 3, 2), (6, 2, 1), (5, 1, 3)이다.

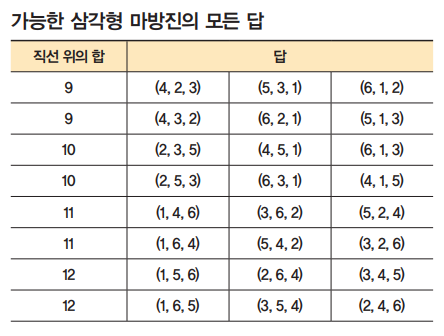
답별로 순서쌍을 모두 이어 붙이면 9자리의 수를 만들 수 있는데, 이 중에서 가장 큰 수는 432621513이다. 이처럼 오각형 마방진에 채운 1~10까지의 수를 이어붙이면 16 또는 17자리의 수가 만들어진다. 이 중에서 가장 큰 16자릿수를 찾는 사람이 이기는 대결이다.

오각형 마방진에 숨겨진 규칙

오일러와 최석정은 너도나도 종이에 숫자를 써가며 고민하기 시작했다. 대결을 지켜보던 학생들도 풀기 시작해 몇 가지 규칙을 찾아냈다. 

먼저 1부터 10까지의 숫자를 차례대로 나열하면 총 11자릿수가 된다. 16자릿수를 만들기 위해서는 중복으로 들어가는 노란색 오각형 위의 수들을 연결한 수가 5자리여야 한다. 따라서 이 수는 모두 1자리여야 하므로 10은 여기에 들어갈 수 없다. 

또 가장 큰 16자릿수를 찾기 위해서는 오각형 바깥에 들어가는 수들 중에 가장 작은 수는 되도록 커야 한다. 따라서 10부터 수가 큰 순서대로 5개의 수를 바깥쪽에 둬야 6으로 시작하는 큰 수를 만들 수 있다. 그리고 나머지인 1부터 5까지의 수는 노란색 오각형에 배열돼야 한다. 이렇게 손으로 써 가며 답을 찾을 수 있지만, 노란색 오각형에 수를 배치하는 경우의 수를 모두 따지자면 시간이 오래 걸린다. 

한편 오일러와 최석정의 대결과는 상관없는 한 학생이 코딩으로 가장 빨리 답을 찾아 세기의 대결이 흐지부지 끝나버렸다. 이렇게 마방진의 고수는 컴퓨터가 돼버렸다. 조금 씁쓸하지만 어떻게 답을 찾았는지, 다음 장에서 배워보자.

▲ PDF파일에서 고화질 이미지를 확인할 수 있습니다.