d라이브러리

동그라미와 세모, 네모, 동그라미, 세모 그리고 다음은? 아마 네모겠죠? 뚜껑을 따자마자 규칙을 찾아 주는 ‘함수’맛 통조림이 나왔습니다. 식과 그래프 소스로 깊은 맛을 더한 신제품 ‘함수’맛 통조림, 지금 바로 따 볼까요?


함수는 초등학교 1학년 과정에서 100까지의 수 배열표에서 수의 규칙을 찾는 활동으로 처음 만납니다. 2학년 때는 여러 가지 물체와 무늬의 다양한 변화에서 규칙을 찾고, 3학년 때는 규칙을 정하여 한 가지 도형으로 여러 가지 무늬를 만드는 활동을 합니다. 4학년 때는 규칙을 말이나 글로 표현하는 방법을 공부합니다. 5학년 때는 밀기와 뒤집기, 돌리기 등의 방법을 이용해 한 가지 무늬로 새로운 무늬를 만들어 봅니다. 6학년 때는 두 양 사이의 비와 비율의 의미와 비례식을 이해하여 활용하는 방법을 배웁니다. 중학교 때는 본격적으로 함수의 개념에 대해 공부합니다. 순서쌍과 좌표를 이해하고 함수를 표와 식, 그래프로 나타내는 연습을 합니다.


규칙, 왜 찾아야 하는 거지?

“도대체 왜 봉투가 더 필요하다는 거야?”
“내가 지난번에 책 4권을 이 봉투에 넣었는데 봉투가 찢어졌거든! 3권은 괜찮았는데…. 그런데 네가 지금 그 봉투에 10권을 넣으려고 하잖아!”
“그래서 봉투 2개를 겹쳤다니까!”
“봉투 2개가 아니라 4개가 필요하다고!”

봉투와 책 사이에는 어떤 관계가 있는 걸까요? 사실 봉투의 수에 따라 찢어지지 않고 넣을 수 있는 책의 개수는 정해져 있습니다. 이번에 만나게 될 주제는 이처럼 주변에서 만날 수 있는 어떤 관계에 대한 이야기예요. 앞서 살펴본 봉투와 책 사이의 관계 같이 일상생활 속에서 만나는 관계나 규칙은 우리가 학교에서 배우는 ‘함수’와 관련된 것입니다.

초등학교에서는 수와 식, 도형의 무늬에서 규칙을 찾는 연습을 통해 문자와 기호를 사용하여 양 사이의 관계를 표현하는 것을 연습합니다. 특히 5~6학년 때 배우는 비와 비례는 중학교에서 공부하는 함수 단원과 연결되는 중요한 개념입니다. 이는 나아가 고등학교에서 수열의 규칙을 찾는 내용으로 발전하게 됩니다.

함수는 대수나 기하 영역에 속하지 않고 이들을 이어 주는 역할을 합니다. 이제 수학의 발전과 통합의 핵심적인 역할을 담당했던 함수를 만나러 떠나 볼까요?


만남1 규칙 찾기
 

초등학교 1~2학년 때는 ‘100까지의 수’ 단원과 ‘곱셈구구’ 단원의 소단원 ‘규칙 찾기’와 ‘규칙을 찾을 수 있어요’ ‘곱셈표에서 규칙을 찾을 수 있어요’를 통해 처음으로 ‘함수’의 개념을 이해하기 위한 기초 공부를 시작합니다. 주로 ‘수 배열표’와 ‘곱셈표’를 이용하며 기본 도형의 일정한 배열에서 규칙을 찾아 문제를 해결하는 연습을 합니다.
 

만남2 규칙적인 무늬 만들기
 

초등학교 3학년이 되면 일정하게 나열된 도형에서 모양의 규칙을 찾는 활동에서 스스로 기본 도형을 정하고 규칙을 만드는 활동으로 발전합니다. 또 달력이나 시계를 도구로 사용하여 일정한 규칙성을 발견하고 날짜와 시각을 알아보는 활동도 합니다. 수의 규칙성을 포함하고 있는 달력을 이용하여 당장 눈에 보이지 않는 다음 수를 찾아보는 활동입니다.
 

만남3 관계를 식으로 나타내기
 

초등학교 4학년이 되면 하나의 수 또는 도형의 나열에서 벗어나 연속된 두 개 이상의 수 또는 도형에서 관계와 규칙을 찾는 활동을 합니다. 또한 둘 사이의 관계를 식으로 나타내기도 합니다. 이러한 활동은 5~6학년 과정의 비와 비례, 비례식 단원으로 발전합니다. 두 양 사이의 관계에서 한 쪽이 변하면 동시에 다른 쪽도 함께 변하는 관계를 배우고, 이에 따른 ‘비’를 공부하게 됩니다.

더 나아가 내년부터 바뀌는 6학년 교육과정에서는 이러한 대응 관계를 문자를 사용하여 식으로 표현하도록 합니다. 특히 비례관계를 정비례와 반비례 관계로 구분해 배우며 관계를 표나 식으로 나타내는 공부를 하게 됩니다.


만남4 다양한 함수의 뜻과 그래프
 

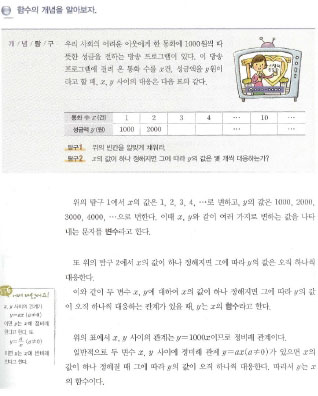
초등학교 6학년 때 공부했던 비례식의 개념은 정비례와 반비례 함수식을 이야기 하며 함수로 발전합니다. 중학교 1학년이 되면 본격적으로 함수의 개념을 배웁니다. 한 쪽의 값이 변함에 따라 다른 쪽의 값이 정해지는 둘 사이의 대응 관계를 이용합니다. 특히 대응 관계를 표와 그래프를 이용해 관계를 눈으로 확인할 수 있게 됩니다.

이러한 함수의 기본 개념을 바탕으로 순서쌍과 좌표를 이해하고 그래프를 공부합니다. 또 실생활에서 함수가 이용되는 예를 배우며 함수에 대한 이해를 높힙니다. 학년이 올라감에 따라 일차함수와 이차함수의 뜻과 성질을 배우고 그 그래프를 공부합니다. 방정식과 함수의 관계에 대해서도 배웁니다.


변화, 어떤 관계가 있는 거지?

밤하늘에 빛나는 별의 밝기와 거리 사이의 관계, 태양과 달 사이의 관계를 통해 과학자들은 어떤 미래를 예측할까요? 학교에서 집까지 걸어갈 때와 뛰어갈 때 걸리는 시간이 달라지는 이유를 수학적으로 나타낼 수 있나요?

이처럼 우리 일상생활 속에서 규칙성을 발견하고 이해하면 다음에 어떤 일이 일어날지 예측할 수 있게 되는 능력이 생겨요. 바로 함수 때문에 가능한 것입니다. 지금부터 우리가 왜 ‘규칙성’과 ‘함수’에 대해 배워야 하는지 알려 드릴게요.


이유1 변화하는 현상을 이해하고 예측하기 위해서

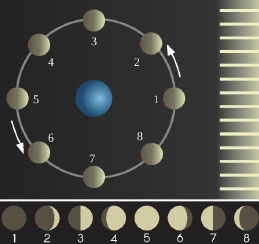
태양과 달이 주기적으로 변하는 현상과 달의 운동에 따라 밀물과 썰물이 생기는 현상은 이미 역사적으로 오래 전에 밝혀진 사실이에요. 이렇게 규칙적으로 반복되는 태양과 달의 움직임을 관찰하면 우리는 보름달이 언제 뜨는지, 썰물과 밀물이 언제 일어나는지, 내일 해가 언제 뜨고 지는지 등 둘 사이의 관계를 이해하고 앞으로 일어날 일을 보지 않고도 예측할 수 있게 됩니다.

함수를 통해 주변의 상황을 이해한다는 것은 어떤 변하는 두 양 사이의 관계를 알게 되는 거예요. 더 나아가 기호를 사용해 식으로 나타내기도 합니다.

함수는 변하는 현상을 관찰하고 예측하는데 많은 도움을 줍니다. 만약 수학이 없다면 둘 사이에 어떤 관계가 있다는 것만 알 수 있을 거예요. 같은 관계라 하더라도 상황에 따라 다르게 해석하거나 비교할 수 없을 것입니다.

하지만 수학적으로 분석하고 해석함으로써 나타낸 식을 이용해, 둘 사이 관계를 비교할 수 있고 더 복잡한 관계로 발전이 가능한 것입니다. 이러한 함수의 개념을 어렵게 생각하지 마세요. 어떤 사물에 이름을 붙이거나 전화번호를 정하는 것, 우리가 살고 있는 집 주소 등 우리는 이미 생활 속에서 함수를 사용하며 살아가고 있으니까요.
 

이유2 수학을 더 잘 이해하기 위해서

함수는 역사적으로 수학의 발전과 통합에 중요한 역할을 했습니다. 수학은 크게 대수와 기하 영역으로 나뉩니다. 대수 영역에서는 수와 연산, 문자를 주로 공부하고 기하 영역은 도형을 다루는 부분입니다.

함수는 이 두 영역을 함께 공부하는 것을 가능하게 합니다. 예를 들어 기하 영역에서 배우는 도형을 좌표평면에 옮겨 그래프를 그리고 대수 영역의 식을 구하는 활동으로 두 영역을 동시에 공부할 수 있게 하는 것입니다. 초등학교에서부터 배우는 다양한 연산은 함수의 기초가 됩니다. 고등학교에서 배우는 확률 함수나 정규 분포도 모두 함수와 관련됩니다. 함수는 초등학교 때부터 배운 기초 연산에서 고등학교 수학 과정까지 알게 모르게 수학을 이해하도록 도와 주는 역할을 하고 있습니다.
 

교과서와 문제집 속에 숨은 의미와 그림자 찾기!

수학 교과서는 정말 중요한 정보를 가득 담고 있습니다. 때로는 그 정보가 보이지 않을 수도 있지만요. 자! 그러면 평소에 잘 보이지 않던 정보와 재미난 활동을 찾아볼까요? 이번 기회에 다른 관점으로 깊게 생각해 보는 시간을 가져 보세요. 여러분의 사고력이 한 단계 업그레이드 될 거예요.


초등학교 수학 교과서 4-2 120쪽
 

초등학교 저학년 때는 어떤 규칙성을 이해하고 예측하는 과정에 초점을 두고 4학년이 되면 수로 표현된 두 양 사이의 관계를 교과서에서와 같이 ♤와 ▣사이의 관계를 식으로 표현합니다. 그리고 중학교 1학년때는 함수를 ‘두 변수 x, y에 대해서 x의 값이 하나 정해지면 그에 따라 y의 값이 오직 하나씩 대응하는 관계가 있을 때, y는 x의 함수’라고 정의합니다. 여기서 중요한 것은 어떤 체계적인 규칙만을 함수라고 말한다는 점입니다. 제시된 교과서에서는 y가 x의 함수인 것을 기호로 y=f(x)와 같이 나타냅니다.

역사적으로 보면 함수는 수학적으로 어떤 대상의 변화를 설명하기 위한 도구로 만들어졌습니다. 그러나 학생들은 움직이는 물체 사이의 관계를 함수라고 생각하기보다는 교과서에서 배우는 식으로 만들어진 관계만 함수라고 생각합니다. 따라서 우리는 규칙성을 바탕으로 함수를 공부하고 있지만 함수가 될 수 있는 다양한 관계를 상상할 수 있어야 합니다.


중학교 2학년 지학사 수학 교과서 116쪽
 

우리는 함수를 표와 함수식 또는 그래프가 전부라고 생각합니다. 하지만 이는 함수의 전부가 아니라 함수를 표현하는 다양한 방법 중 하나임을 잊지 말아야 합니다.

예를 들면 교과서에 주어진 y=2x라는 일차식을 보고, 단순히 함수식이라는 것 외에 x=1일 때, y=2의 값을 갖는다는 정보도 놓치지 말아야 합니다. 또 이 함수식으로 어떤 그래프가 그려지는지, 값에 따라 어떤 규칙을 갖는지 등 다양한 정보를 생각해 보아야 합니다.

표의 경우도 마찬가지입니다. 단순히 표에 나온 내용을 함수라고 생각한다면 일정하게 적어놓은 수의 나열도 함수라고 잘못 생각할 수 있으니 조심해야 합니다. 이러한 작은 생각들이 여러분을 함수 박사로 만들어 줄 것입니다.


중학교 9-가 디딤돌 수학 교과서 117쪽
 

우리는 일상생활 속에서 함수가 이용되는 것이 어떤 것인지 생각해 볼 수 있어야 합니다. 다음은 중학교 3학년에서 배우는 이차 함수에 관한 내용입니다. 교과서는 문제보다 앞서 실제 상황을 설명하고 있습니다. 비행기에서 뛰어내릴 때 걸리는 시간에 따라 변하는 거리를 함수로 만들고 이를 표와 함수식으로 만든 실제 예를 통한 문제입니다. 이처럼 우리는 걸음을 걸을 때도 시간에 따른 걸음의 함수를 생각해 보는 훈련이 필요합니다.


역사, 그리고 실생활 속의 통계​

함수의 유래

주말에 아빠와 자동차를 타고 가며 자동차의 속도 계기판을 봅니다. 할머니 댁까지 가는 데 걸리는 시간이 속도에 따라 달라진다는 것을 알게 됩니다. 지난 주엔 친구와 공원에 날아다니는 나비를 보며 시간이 지남에 따라 그 수가 증가한다는 것을 알게 되었습니다.

이처럼 함수는 학교에서만 배울 수 있는 단순한 학문이 아닙니다. 실생활 곳곳에서 발견되는 어떤 둘 사이의 관계가 모두 함수로 표현될 수 있습니다.

함수는 고대 바빌로니아표(곱셈표, 역수표, 제곱과 세제곱표, 지수표)에서 시작됩니다. 함수의 유래는 천문학과 관련된 것으로 추측합니다. 달과 별 등의 천체 주기를 관찰하고 관찰된 위치의 주기적인 변화를 연구한 것에서 시작했습니다.

17세기쯤 여러 가지 운동 연구에서 지금 사용하는 함수의 개념이 도입됐습니다. 이탈리아의 과학자 갈릴레오 갈릴레이는 일정한 속도로 움직이는 물체는 물체가 움직인 거리와 그 거리까지 움직이는 데 걸린 시간의 제곱에 비례한다는 것을 관찰했습니다. 이와 같이 자연 현상에 따라 변하는 값들 사이의 관계를 탐구하고, 관찰된 현상을 식으로 만들어 수학적 모델링을 하는 데 함수의 개념이 사용된 것이 함수의 유래입니다.


영화 속 함수

고대 천문학과 수학, 건축 등 많은 분야에서 놀라운 업적을 남긴 마야 문명엔 무서운 예언인 종말론이 있습니다. 그들은 지구가 5125년을 대주기로 돌아간다고 믿었고 그 주기에 따라 제작한 것이 마야 달력이었습니다. 주기적으로 나타나는 변화를 근거로 기원전 3114년 8월 13일을 시작으로 2012년 12월 21일 지구의 주기가 끝난다고 미래를 예측한 것입니다.

지난 2000년, 미국의 과학자 테렌스 메케나는 중국 주역의 점괘를 수리적으로 분석해 함수로 나타내 보았더니 2012년 이후의 그래프가 없다는 것입니다. 이러한 배경은 우리의 상상을 자극해 영화 ‘2012’와 같은 이야기를 만날 수 있게 했습니다. 2009년에 감독 롤랜드 에머리히가 이를 배경으로 영화를 만든 것입니다. 이 영화에서는 양자역학을 기초로 태양폭발이 일어나며 중성자 반응으로 지구 내부의 핵이 달구어지면서 지각이 심하게 흔들리는 거대 지진이 일어날것이라는 이야기를 합니다. 또한 지각 변동으로 생겨난 거대한 쓰나미에 의해 육지가 모두 물에 잠길 것이라는 과학적 가설로 종말론을 뒷받침하고 있습니다.

이는 인도의 물리학을 전공한 어느 과학자에 의해 온도 변화와 그에 따른 주기적인 지각변동 연구를 기초로 상황을 예측한 것입니다. 이때 시간에 따른 지구 내부 핵의 온도 변화와 지각 변동의 관계도 바로 함수로 설명할 수 있습니다. 이처럼 영화와 역사, 그리고 우리 주변에 많은 현상들을 함수로 설명할 수 있습니다.