d라이브러리

얼마 전 독자를 만난 피터팍은 “제가 아무리 대충 만들어도 그것보단 잘 만들 것 같아요”라는 말을 듣고 실의에 빠졌다. 모든 요리가 어렵게 보여 다음 아이템을 찾지 못하고 공원에 숨어있던 피터팍. 누군가 말을 거는 소리에 돌아본다. “무슨 일인지 모르겠지만 내 피크닉 요리를 나눠줄 테니 기운 내게.” 그 음식을 본 피터팍은 외쳤다. “이거다! 다음 요리는 이걸로 정했어!”

팀 원들이 싸우지 않게 햄 샌드위치를 한 번의 칼질로 정확히 반으로 잘라야 하는데 과연 가능할
까요? 아주 쉽다고요? 여러분이 떠올린 건 흔히 보는 삼각기둥 샌드위치 반쪽일 거예요. 맞아요.
직육면체 샌드위치라면 대각선 방향으로 칼질을 하면 한 번에 반으로 자를 수 있어요.

하지만 토스트용 식빵처럼 일정하고 네모난 모양이 아닌 샌드위치라면 어떨까요? 한쪽 빵은 삼
각기둥이고 다른 한쪽 빵은 누군가 귀퉁이를 뜯어 먹어서 이빨 자국난 울퉁불퉁한 모양이고 가운데 들어간 햄은 삐뚤어진 타원 모양이라면요? 그런 샌드위치 재료를 마구잡이로 쌓아도 한 번의 칼질로 정확하게 반으로 자를 수 있을까요? 이 문제를 해결하는 것이 바로 ‘햄 샌드위치 정리’랍니다.

솔로몬의 선택, 햄 샌드위치 정리

햄 샌드위치 정리는 ‘n차원 유클리드 공간에 놓인 양의 부피, 혹은 면적을 가진 n개의 물체는 n-1차원의 공간으로 자를 수 있다’는 정리예요.

쉽게 말하면 3차원 유클리드 공간에 놓인 3개의 물체를 한 번에 반으로 자르는 2차원 평면이 있다는 것이고, 2차원 유클리드 공간에 놓인 2개의 물체는 1차원 직선으로 한 번에 반으로 자를수 있다는 거예요. 반으로 자른다는 건 모든 물체가 각각 넓이나 부피가 반이 되도록 나뉘는 걸 말하고요. 간단해 보이는 이 정리가 왜 어려운지 예시를 통해 좀 더 살펴볼까요?

위 그림과 같이 빵 2장과 햄 1장을 가지고 샌드위치를 만들어 볼게요. 먼저 아주 곱게 차곡차곡
쌓았습니다. 이걸 반으로 자르는 건 간단해요. 세로로 2등분 지점에 칼질을 해도 되고 대각선으로
잘라도 되겠군요. 그럼 오른쪽 샌드위치를 정확히 반으로 자르려면 어떤 모양으로 칼질을 해야
할까요?

샌드위치를 놓고 칼을 들어봅시다. 여러분은 위험하니까 빵 칼을 준비해주세요. 먼저 샌드위치를
하나도 가리지 않는 왼쪽편에 칼을 둬요. 그러면 샌드위치는 0:100으로 분배된 상태가 되죠. 이번
엔 칼을 완전히 오른쪽에 가져갑니다. 그러면 샌드위치는 100:0으로 분배된 상태예요.

이제 칼을 천천히 움직여 빵 위 어딘가에서 방향을 맞추고 칼의 각도를 기울여 봅시다. 아마 수
많은 경우의 수를 움직이다 보면 50:50으로 정확히 분배하는 방향과 각도가 분명 있을 거예요. 이
것을 증명한 것이 햄 샌드위치 정리랍니다.

다른 차원에서의 햄 샌드위치 정리

그러면 햄 말고도 양상추, 치즈, 오이 등을 넣어 7개의 구성 요소로 쌓은 샌드위치를 7차원으로 가
져가면 6차원의 공간으로 자를 수 있을까요? 안타깝게도 답은 “NO”예요. 우리가 3차원 공간에서 만든 샌드위치는 7차원에서 부피가 0이 되거든요. 평면에 그린 사각형의 면적이 2차원에서 양수더라도 3차원 공간에 집어넣으면 부피가 0이 되는 것과 같은 원리지요.

따라서 단순히 샌드위치를 7장 쌓았다고 7차원 공간에서 6차원 공간으로 자를 수 있는 건 아니에
요. 하지만 7차원 세계의 물체를 7개 쌓으면 6차원 평면 칼로 자를 수 있어요. 어떤 모양일지 상상
하긴 무척 어렵지만요!

다만 7개의 내용물이 든 3차원에 있던 샌드위치를 7차원에 넣었을 때의 답을 근사적으로는 찾
을 수 있어요. 3차원 샌드위치를 7차원에서 두께를 갖도록 4차원만큼 더 부풀려 7차원 유클리드 공간에 넣고 6차원 공간으로 자른 뒤 해를 3차원에 대응시키는 거예요. 쉽게 설명하면 평면에 팬
케이크(2차원 평면으로 가정)가 3장 놓여있을 때 이것들을 3층으로 쌓고 두께를 약간 부풀리면 돼
요. 이 부풀려진 팬케이크는 부피가 0이 아니므로 3차원 햄 샌드위치 정리로 답을 찾을 수 있어
요. 그 다음 잘린 3장의 팬케이크를 2차원 평면에 대응하면 근사적인 답을 얻을 수 있죠.

집합에서도 쓸 수 있다

그런데 이런 햄 샌드위치 정리는 물체에만 쓸 수 있는 게 아니에요! 이산수학에서는 집합을 정확
히 반으로 나눌 때도 햄 샌드위치 정리를 활용해요. 아래 그림을 보면 파란색 점과 빨간색 점이 흩
어져 있죠? 이를 빨간 점들의 집합과 파란 점들의 집합으로 나눠 생각한다면 평면에 놓인 2개의 집합을 정확히 반으로 나누는 직선이 반드시 있다는 것 역시 햄 샌드위치 정리로 설명할 수 있어요.

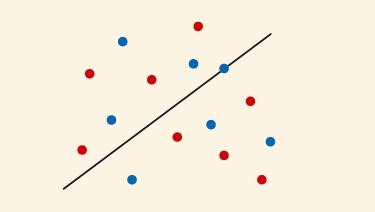
이산수학에서 점들의 집합의 부피는 점의 개수로 정의되기 때문에 똑같은 원리를 적용할 수 있
고, 점들이 아무리 뿔뿔이 흩어져 있어도 직선 하나로 2등분할 수 있어요. 물론 이 경우에도 3개의
집합이 흩어져있다면 각각 반으로 나누는 직선은 없을 수 있어요. 모양을 가진 물체뿐만 아니라 집
합에서도 적용할 수 있다니 정말 유용하죠?

햄 샌드위치 정리는 1968년 폴란드 수학자인 휴고 스타인하우스가 처음으로 제시했고 1942년 영
국 수학자 아서 해롤드 스톤과 미국 수학자 존 튜키가 n차원에서 증명했어요. 그 덕에 저는 팀 원
들에게 아주 공평하게 피터팍의 샌드위치를 나눠줄 수 있겠어요! 기뻐할 수학동아 편집팀의 모습
이 눈에 선하네요. 후훗.

햄 샌드위치 정리에는 한 가지 맹점이 있습니다. n차원의 어떤 복잡한 경우에도 반드시 해가 있지
만, 그 해를 햄 샌드위치 정리가 찾아주지는 않는다는 거예요. 해를 구하는 것은 컴퓨터를 이용하
거나 다른 방법을 통해 계산해야 해요. 저는 칼 한자루만 들고 감으로 잘라야 해서 여러 번 시행착
오를 거쳐야 했답니다. 팀 원들의 표정을 보면 누가 더 큰 조각을 받았는지 검증할 수 있을 것 같습니다. 

도움 박경배(서울대학교 수리과학부 연구교수), 성찬영(한국교원대 수학교육과 교수)