d라이브러리

예술이 꽃 피운 시기를 물으면 흔히 이탈리아를 기반으로 한 르네상스 시대를 떠올리곤 하죠. 정교하고 섬세한 그림으로 유명한 르네상스 회화는 후대의 예술가들에게 영감을 줍니다. 그리고 수많은 예술가들을 홀린 르네상스의 그림 그리는 법에는 ‘수학’이 있습니다. 수학적으로 그림 그리는 법을 알아 봐요.

멋진 광경을 그림으로 남겨보고 싶고 생각한 적이 있나요? 혹은 가족이나 친구들과 보낸 행복한 순간을 사진이나 그림으로 남겨 영원히 간직하고 싶다고 생각해 본 적은요? 
만약 그런 생각한 적이 있는 분들이라면 오늘 잘 오셨습니다. 오늘은 실제 모습 그대로 그림으로 표현하는 법을 알려드릴 거예요. 그림을 사실적으로 표현하려면 무엇이 중요할까요? 여러 요소가 두루 중요하겠지만 그중 하나는 공간을 표현하는 방법입니다. 우리가 사는 3차원 공간의 모습을 2차원 평면에 나타내야 하니, 평면에서도 공간감을 느낄 수 있게 그려야겠지요. 하나의 그림에서 어떤 물체는 가까이 있고, 어떤 물체는 멀리 있는 것처럼 느껴진다면 공간감이 잘 반영된 그림입니다. 

위 그림을 보세요. 한 화면에서 나무는 눈앞에서부터 시작해 길따라 점점 멀어지고, 건물들은 저 멀리에 있는 것 같습니다. 이런 기법이 언제 시작됐는지 아시나요? 바로 르네상스 시대입니다. 거리감을 표현하기 위해 르네상스 작가들은 ‘원근법’이라는 수학적인 방법을 이용해 그림을 사실적으로 묘사했습니다. 

공간을 표현하는 원근법

원근법은 15~16세기 르네상스 시대부터 본격적으로 회화에 이용됩니다. 물론 기존에도 원근법은 있었지만 잘 이용하지 않았습니다. 그러다 15세기 초 이탈리아 건축가 필리포 브루넬레스키가 수학을 이용해서 원근법을 체계적으로 개발한 이후 르네상스 시대에 본격적으로 원근법을 이용했습니다. 덕분에 미술은 인류 최대의 황금기를 맞이했지요. 
원근법의 종류는 다양합니다. 예를 들어 색의 심리 효과를 이용해 원근감을 표현하는 ‘색채 원근법’이 있습니다. 심리적으로 적극적인 인상을 주는 빨강은 가까이 있는 물체에, 소극적인 인상을 주는 푸른색은 먼 물체에 입혀 원근감을 표현하지요. 
원근법 중에서 가장 과학적이고 수학적인 방법은 ‘선 원근법’ 혹은 ‘투시 원근법’입니다. 화가의 눈을 한 점에 고정한 뒤, 그 시점을 기준으로 물체를 마치 카메라로 찍어내듯이 그려내는 것이지요. 그래서 기준이 되는 시점뿐 아니라 실제 거리에 따른 비율이 굉장히 중요합니다.
이탈리아 화가 마사초는 ‘성 삼위일체’에 원근법을 활용했습니다. 작품 속에 인물을 실제 크기와 거의 비슷하게 그린 뒤, 원근법을 활용해 물체에 거리감을 줘 입체적이고 사실적인 그림을 그려낸 것이지요. 그래서 마사초의 그림 속 예수는 마치 바로 눈앞에 바로 있는 듯 생생하게 느껴집니다. 수학미술관이니 이 원근법을 보다 수학적으로 파헤쳐 봅시다. 

원근법 속 닮음과 비례

 
원근법은 닮음과 비례를 바탕으로 그림을 그리는 방법입니다. 아래 그림처럼 같은 크기의 나무가 한 시점에서 거리의 비가 1:2인 위치에 있습니다. 이 두 나무를 눈 앞에 있는 캔버스에 어떤 비율로 그려야 할까요? 한 시점(O)에서 지면과 평행한 수평면 하나를 그리고, 나무의 끝(A₁, A₂)을 지나도록 직선을 각각 그어 보세요. 그럼 눈 앞에 있는 캔버스에 두 선분 QP와  RP를 그릴 수 있습니다. 

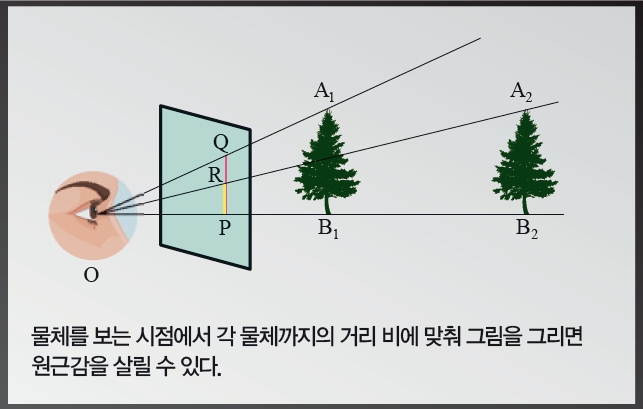
△OQP와 △OA1B1은 대응하는 세 각이 같으니 닮음이고, △ORP와 △OA2B2도 대응하는 세 각이 같아 닮음입니다. 그러니 앞에 서 있는 나무는 QP의 길이로, 뒤의 나무는 RP의 길이로 캔버스에 나타내면 실제와 같은 거리 차이를 표현할 수 있지요. 
점 O처럼 물체의 연장선을 한곳으로 모았을 때 선과 선이 만나는 점을 ‘소실점’이라 합니다. 원근법을 이용한 회화에서는 이 소실점이 확연히 드러나지요. 소실점을 기준으로 선을 연장하고, 그 선을 기준으로 입체를 표현하는 방법을 투시 원근법, 혹은 투시도법이라고 합니다. 

공간감각 살리는 투시도법

투시도법의 종류는 소실점의 개수에 따라 1점 투시, 2점 투시, 3점 투시 등으로 나뉘며 경우에 따라 4점 투시도 있습니다. 기차가 다니는 철도나, 양옆으로 가로수가 늘어져 서 있는 길처럼 시점이 하나로 모여드는 그림을 본 적이 있을 거예요. 이게 바로 1점 투시법을 이용해 그린 겁니다. 2점 투시법과 3점 투시법을 이용할수록 공간의 입체감을 더욱 살릴 수 있지요.
특히 1점 투시법은 그림 혹은 화면을 보는 사람의 시선을 한 곳으로 모을 수 있어 재밌습니다. 한 곳으로 시선을 모으면 몰입도가 올라가, 긴장감을 고조시킬 수 있거든요. 그래서 이 수학적인 표현 기법은 영화를 만들 때도 쓰입니다. 
역사상 가장 완벽하고 혁신적인 영상을 만들어낸 거장으로 뽑히는 영화감독 스탠리 큐브릭의 영화는 1점 투시법을 이용해 촬영한 것으로 유명합니다. 직사각형의 영화 화면에 대각선 두 개를 그어 보세요. 그럼 영화가 소실점을 중심으로 촬영됐다는 사실을 알 수 있습니다. 이 기법은 수많은 영화 제작에 영향을 줬습니다.
이제 오늘 전시에 등장한 멋진 그림들을 다시 한번 보세요. 이제껏 설명한 원근법의 원리가 조금은 보이지 않나요? 여러분도 오늘 배운 그림 그리기로 기본기를 닦아 본인만의 멋진 그림을 그려 보세요.