d라이브러리

오늘은 동글동글한 몸에 털이 잔뜩 나있는 종족이 모여 사는 동글동글 왕국 납세의 날입니다. 빗질해서 때 생기는 가마의 수대로 세금을 내야하지요. 그때 가마가 없다고 주장하는 자가 나타나 소란을 핍니다. 몸이 꼭 완벽하게 동그랗지 않더라도 동글동글 종족은 가마가 2개씩 있는 건 누구나 아는 사실인데, 무슨 일일까요?

“억울하옵니다! 저는 가마도 없는데, 어찌 서리태 두 포대를 세금으로 내란 말입니까!"

“무엄하도다! 가마가 항상 하나 이상 있다는 건 수학적으로도 증명이 가능한데, 어찌 손바닥으로 하늘을 가리려고 하느냐! 뭣들 하느냐, 어서 이놈의 목을 쳐라!”

반발하는 백성에 왕이 노했지만, 가마가 없다고 주장하는 자는 멈추지 않았습니다.

“어느 안전이라고 제가 거짓을 고하겠습니까. 저는 사실을 말할 뿐입니다.”

“좋다. 지금 당장 증명해 보이겠다. 반박할 수 없으면 네 목을 칠 것이고, 만약 내가 틀렸다면 왕위에서 물러날 것이다!” 왕은 왕좌를 내걸고 왕국의 모든 일을 수학으로 설명하는 수설이를 불러옵니다. 수설이는 어렵게 말을 꺼냅니다.

“아뢰옵기 황송하오나….”

가마가 없다고 주장하는 백성의 주장은 ‘푸앵카레-호프 정리’로 따질 수 있습니다. 이 정리는 프랑스 수학자 앙리 푸앵카레와 독일 수학자 하인츠 호프의 이름을 딴 겁니다. 도형 위에 연속적인 벡터장이 있을 때, 즉 동글동글 종족처럼 털이 조밀하게 있을 때 ‘벡터장의 지수’가 ‘오일러 지표’와 똑같다는 신비로운 정리지요. 

털은 방향과 크기가 있어 털 한 올은 하나의 벡터라 볼 수 있습니다. 그리고 벡터장은 이런 벡터들이 모여 있는 영역을 말합니다.

먼저 오일러 지표부터 말씀 드리겠습니다. 오일러 지표는 v를 꼭짓점, e를 모서리, f를 면의 수라고 할 때 ‘v-e+f ’값을 말합니다. 위상수학적 성질이 같은 도형끼리는 항상 같은 오일러 지표를 갖지요. 즉 삼각뿔, 직육면체와 같은 모든 다면체는 구와 위상적으로 같아 그 모양에 관계없이 오일러 지표는 늘 2가 됩니다.

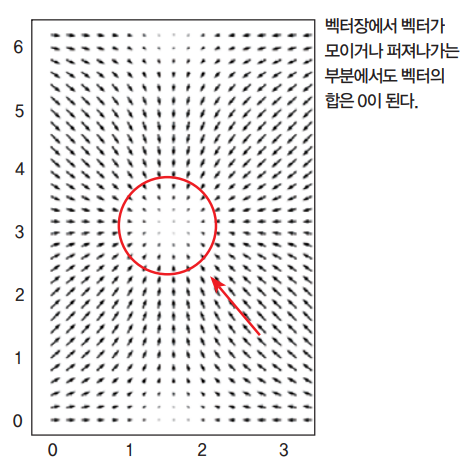
이제 오른쪽 그림처럼 평면의 한 점으로 모든 벡터가 모이는 벡터장을 떠올려 보시지요. 크가 같고 방향이 다른 두 벡터를 합하면 0이 되기 때문에 가마, 혹은 소용돌이처럼 보이는 부분의 벡터 합은 0이 됩니다. 

벡터장의 지수는 이처럼 벡터 합이 0인 점(영점) 주위에 있는 벡터들이 어떤 형태로 퍼져 있는지 알려주는 숫자입니다. 벡터들이 시계방향으로 뱅글뱅글 돌고 있다면 지수가 1, 즉 가마가 한 개 있다면 벡터장 지수의 합은 1이지요. 지수가 2일 때는 시계방향으로 도는 원이 양쪽에 2개 있을 때입니다. 

구 위에 나타나는 쌍가마

동글동글 종족처럼 동그란 구는 오일러 지표가 2입니다. 푸앵카레-호프 정리에 의해 벡터장의 지
수도 2이기 때문에 구에서는 반드시 쌍가마가 나타나게 되지요. 이 경우를 특별히 ‘털난 공의 정리’라고 부릅니다. 즉 털이 촘촘하게 나 있는 공을 모든 점에서 가마 없이 빗는 게 불가능하다는 정리입니다. 

털난 공이라고는 했지만 그것이 꼭 공일 필요는 없습니다. 위상수학에서는 구멍을 뚫거나 찢지만 않으면 같은 도형이기 때문입니다. 따라서 공을 찌그러뜨려도 가마는 늘 2개입니다. 

이 문제는 지구 위 모든 곳에서 동시에 바람이 불게 할 수 있는가의 문제로 바꿀 수도 있습니다. 
털난 공의 정리를 대입해보면 지구는 구의 형태이고, 벡터의 지수가 2일 테니, 두 곳에 벡터 합이 0이 되는 곳이 생겨 바람이 불지 않는 두 장소가 늘 있습니다. 

물론…, 가마 없는 빗질이 가능한 경우도 있습니다. 도넛 모양의 토러스의 경우 오일러 지표가 0이기 때문에, 벡터의 지수도 0입니다. 토러스는 가마 없이 매끄럽게 빗질이 가능하다는 것이지요. 그런데 전하, 아뢰옵기 황송하오나…, 저 자의 배가 뻥 뚫려있습니다.