d라이브러리

작대기가 길어도 실처럼 가늘다면 아주 좁은 공간에서도 작대기를 휘지 않고 한 바퀴 돌릴 수 있다고 합니다. 그렇다면 방에 가까스로 들어가는 큰 가구는 어떨까요? 최근 우리나라를 포함한 다국적 연구팀이 가구를 돌릴 묘수를 내놨습니다.

화장실처럼 좁은 공간에서 길이 1m인 작대기를 한 바퀴 돌리려고 합니다. 이게 가능한 방 모양 중에 넓이가 가장 작은 건 얼마일까요?

1917년 일본 수학자 가케야 소이치가 만든 문제로, ‘좁은 공간에서 갑자기 공격을 받은 사무라이가 창을 한 바퀴 돌려서 공격할 때 필요한 최소 넓39이는 얼마인가’로 소개하기도 합니다.

문제를 단순하게 만들기 위해 방과 작대기를 2차원의 평면 위에 둡시다. 작대기의 중심을 잡고 돌린다면 방의 모양이 지름이 1m인 원이니까 넓이는 π/4m2이 됩니다. 조금만 생각해 보면 더 작은 방도 떠올릴 수 있습니다.

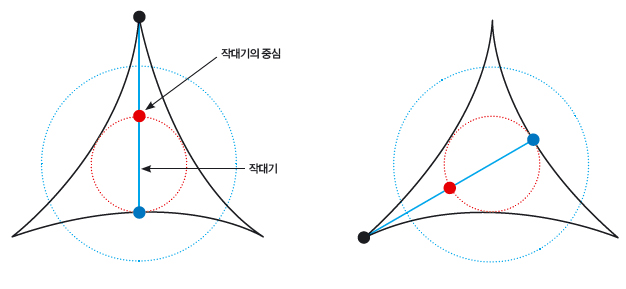
위 그림처럼 작대기의 중심이 작은 원을 그리도록 작대기를 돌리면 작대기 한쪽 끝(검은색 점)이 그리는 자취가 만든 오목 삼각형이 지름이 1m인 파란색 원보다 넓이가 작습니다.

그렇다면 이 방이 최소일까요? 1921년 덴마크-헝가리 수학자 율리우스 팔은 방의 모양이 볼록해야 한다면, 즉 방의 어느 두 점을 잡아도 그 두 점을 잇는 선분이 방 밖으로 삐져나가지 않아야 한다면 높이가 1m인 정삼각형 방의 넓이가

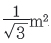
로 가장 작다는 걸 보였습니다.

방의 모양이 볼록하다는 제약이 없으면 어떨까요? 놀랍게도 아주 작은 방에서도 작대기를 돌릴 수 있습니다.

1928년 러시아-영국 수학자 아브람 베지코비치는 0보다 큰 어떠한 c에 대해서도 넓이가 c보다 작은 방을 적당히 잘 만들면 길이가 1인 작대기를 한 바퀴 돌릴 수 있다는 걸 증명했습니다.

예를 들면 40쪽 그림과 같은 방에서도 작대기를 돌릴 수 있습니다. 가는 작대기라 가리키는 방향의 앞쪽과 뒤쪽의 공간은 아주 좁아도 되기 때문입니다. 작대기를 앞뒤로 움직이면서 조금씩 방향을 바꾸는 작업을 계속할 수 있게 방을 만들면 됩니다.

지금까지는 작대기의 두께가 선분처럼 얇을 때 즉 폭이 0일 때 작대기를 돌릴 수 있는 최소 공간의 넓이를 알아봤습니다. 만약 조금 더 두꺼운 작대기를 돌린다면 최소 넓이는 어떻게 바뀔까요?

신기하게도 이 문제에 대한 연구도 이미 있습니다. 폭이 1m고, 높이가 xm(x는 1보다 매우 작은 양수)인 직사각형 작대기를 돌리기 위해서는 넓이가

이상이어야 한다는 것이 증명돼 있습니다.

좁은 방에서 소파 돌리기

이번에는 작대기 대신 소파처럼 좀 더 크고 모양도 다양한 가구를 돌려봅시다. 그런데 이 경우엔 가구 모양이 정삼각형과 정사각형같이 가장 기본적인 도형일 때도 최소 넓이를 갖는 방이 어떤 모양인지 알려지지 않았습니다.

그래서 문제를 다른 관점에서 바라봤습니다. 방의 모양이 볼록할 때 가구를 360°로 돌릴 수 있을 충분조건을 생각해 본 겁니다. 가구를 한 바퀴 돌릴 수 있다면, 가구를 어떤 방향으로 놓더라도 방 안에 들어갈 수 있겠지요? 볼록한 방일 때 가케야 문제를 해결했던 팔은 다음과 같은 문제를 떠올렸습니다.

팔은 1921년에 쓴 논문에서 이같은 질문을 하면서, 마지막 쪽에 덴마크 수학자 하랄 보어가 이 문제의 답은 ‘예’라고 말했다고 적었습니다. 문제는 그 풀이가 적힌 논문을 아직 아무도 찾질 못했다는 겁니다. 과연 풀긴 푼 걸까요? 아니면 찾지 못한 걸까요?

그런데 최근 이 문제가 풀렸습니다. 한국과 슬로베니아, 독일의 다국적 연구팀이 2018년 6월 헝가리 부다페스트에서 열린 계산기하학국제심포지엄에서 문제의 답을 발표했습니다. 아직 학술지에 실린 건 아니지만 이쪽 분야의 권위 있는 학회에서 발표한 겁니다.

배상원 경기대학교 교수와 오트프리트 정(정지원) KAIST 교수, 정 교수의 석사과정생인 최윤성 학생, 삼성디스플레이 소속 윤상덕 박사, 세르기오 차벨로 슬로베니아 류블랴나대학교 교수, 파비안 슈텐 독일 바이로이트대학교 교수는 2017년 일본에서 열린 계산기하 워크숍을 계기로 이 문제를 연구하기 시작했습니다. 그리고 원래보다 더 강력한 문제를 증명했습니다.

연구팀은 가구의 크기를 마음대로 몇 배 늘렸다 줄였다 할 수 있는 신기한 가구가 있다고 가정했습니다. 그리고 가구를 각 θ 방향으로 놓았을 때 가구를 최대 몇 배 늘리거나 줄였을 때 방에 넣을 수 있는지 잰 값을 f(θ), 가구의 중심을 어디로 잡아야 방에 넣을 수 있는지 그 좌표를 알려주는 함수를 (x(θ), y(θ))라고 정했습니다. 이때 f(θ)가 연속함수인 것은 쉽게 알 수 있습니다.

연구팀은 f(θ) 뿐만 아니라 x(θ), y(θ) 모두 연속함수가 되게 잡을 수 있다는 걸 보입니다. 즉 가구를 한 방향으로만 연속적으로 회전시키는 동시에 방 크기에 딱 맞게 확대·축소하며, 가구를 한 바퀴 돌릴 수 있다는 걸 증명한 겁니다.

팔의 문제로 돌아가서 생각해보면 항상 f(θ)≥1 이므로, x(θ), y(θ)로 중심을 움직여가면서 가구를 확대 축소하지 않고 돌리면 가구를 360°로 회전하는 방법이 됩니다. 여러분도 문제가 풀리지 않을 때 관점을 바꿔 생각해보세요. 의외로 쉽게 문제가 풀릴 수도 있습니다.

# 엄상일 교수는 KAIST 수학과를 졸업하고, 미국 프린스턴대학교에서 박사 학위를 받았습니다. 현재는 KAIST에서 강의와 연구를 하고 있습니다. 그래프이론과 이산수학, 조합적 최적화가 주요 연구 분야입니다. 2012년에는 젊은과학자상(대통령상)을 수상했고, 2017년에는 한국차세대과학기술한림원 회원으로 선정됐습니다.