d라이브러리

실베스터-걸러이 정리
평면에 서로 다른 n(n≥2)개의 점이 있다.

모든 점이 한 직선에 있는 것이 아니라면

이 중 정확히 두 점만 지나는 직선이 반드시 있을까?

1893년 영국인 수학자 제임스 실베스터는 위와 같이 질문했습니다. 50년이 지난 1943년 헝가리 수학자 에르되시 팔이 이 문제를 다시 발견하고 미국수학회에서 만든 잡지 ‘월간 아메리칸 매스매티컬’에 소개했지요. 이후 헝가리 수학자 걸러이 티보르가 딱 두 점만 지나는 직선이 반드시 있다는 것을 증명해 흔히 이 문제를 ‘실베스터-걸러이 정리’라고 부릅니다. 이를 통해 다음 정리도 쉽게 증명할 수 있습니다.

더브라윈-에르되시 정리
평면에 n개의 서로 다른 점이 있을 때, 모든 점이 한 직선에

있지 않다면 2개 이상의 점을 지나는 직선이 n개 이상 있다.

왜 그럴까요? 만약 n-1개의 점이 한 직선에 있고, 한 점(점 A)만 다른 곳에 있다면 어떨까요? 점 A와 나머지 n-1개 점을 각각 이으면 직선이 n-1개 생기고, n-1개의 점을 동시에 지나는 직선까지 총 n개의 직선이 있게 됩니다.

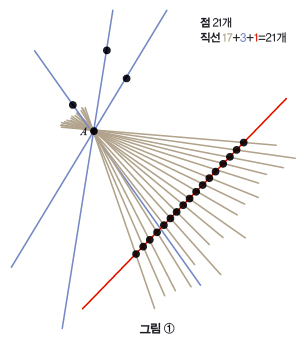
만약 어떤 한 점을 지워도 나머지 모든 점이 한 직선에 없다면 딱 두 점만 지나는 직선에 있는 점 중 하나를 지웁니다. 모든 점이 한 직선에 있을 때까지 이런 점들을 지운 다음 직선에 있는 점들과 밖에 있는 점을 이어 직선을 만듭니다. 그러면 지운 점이 만드는 직선까지 적어도 n개 이상의 직선이 생깁니다.(그림 ① 참고)

1943년 에르되시는 실베스터-걸러이 정리를 쓰지 않고 이 문제를 풀려고 노력했습니다. 결국 1948년 네덜란드 수학자 니콜라스 더브라윈과 함께 문제를 풀어 현재는 이 문제를 ‘더브라윈-에르되시 정리’라고 부르지요.

더브라윈-에르되시 정리는 더 높은 차원으로 확장할 수 있습니다. 2차원 평면이 아닌 3차원 공간에 점이 있고, 그 점으로 결정되는 평면이 몇 개 이상일지 따져보면 됩니다. 이 문제를 정확하게 이해하려면 점이 어떻게 평면을 결정하는지 알아야 하지요.

점 2개는 평면 하나를 결정하지 못합니다. 두 점을 지나는 평면은 무수히 많으니까요. 점 4개가 아무렇게나 있을 때도 불가능합니다. 점 4개를 모두 포함하는 평면이 없을 수 있으니까요.

반면 점 3개가 한 직선에만 없다면 정확하게 하나의 평면을 결정합니다. 카메라를 고정할 때 쓰는 삼각대 다리가 3개인 이유가 바로 이것입니다.

★참고

다소 어려운 개념인 사영공간에 대한 설명을 생략하기 위해 점을 0차원으로 설명했습니다. 본래 사영공간에서는 점이 1차원, 직선이 2차원으로, 이 글에서 설명한 것과 차원을 나타내는 숫자가 1씩 차이 납니다.

따라서 더브라윈-에르되시 정리를 3차원으로 확장한 문제에서는 n개의 점 중 일부 점으로 만들어지는 평면의 수를 물어봅니다.

물론 3차원 공간에 점이 n개 있다고 해서 그 점으로 결정되는 평면이 항상 n개 이상이라고 말할 수는 없습니다. 운이 없다면 n개의 점이 모두 같은 평면 위에 있을 수도 있으니까요. 심지어 모두 같은 직선 위에 있다면 결정되는 평면은 하나도 없습니다.

d차원에서도 더브라윈-에르되시 정리 가능할까?

그런데 1951년 독일 수학자 테오도레 모츠킨은 3차원뿐만 아니라 d차원에서도 더브라윈-에르되시 정리가 가능하다고 증명했습니다. d차원 공간에서 점 n개가 있을 때, 그 점을 모두 포함하는 초평면★이 없다면, 그 점으로 결정되는 초평면이 적어도 n개 이상 있다는 것을 보인 것이지요. 1970년 미국 수학자 커티스 그린은 조건을 하나 더 추가해 문제를 풀었습니다. 먼저 n개의 점을 원소로 하는 집합과 그 점으로 결정되는 초평면의 집합을 정의했습니다. 그리고 점 집합의 원소를 초평면 집합의 서로 다른 원소로 보내는 함수 중에 각점을 그 점을 포함하는 초평면으로 보내는 함수가 있다는 것을 증명했습니다.

초평면★ 유한 차원 공간에서 초평면은 그보다 1차원 낮은 부분 공간을 말한다.

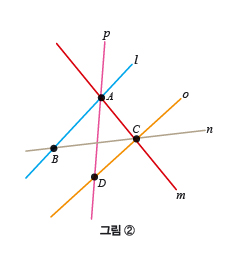
예를 들어 그림 ②와 같이 점이 4개, 직선이 5개 있다면 더브라윈-에르되시 정리를 만족한다는 것을 쉽게 알 수 있습니다. 점 A를 직선 n, 점 B를 직선 l, 점 C를 직선 p, 점 D를 직선 m에 대응시켜 점의 개수보다 직선의 개수가 같거나 많다는 것을 보일 수 있지요. 그런데 그린은 점 A를 직선 p나 직선 l처럼 점 A를 포함한 직선에 대응시켜도, 즉 각점을 그 점을 포함하는 서로 다른 직선으로 대응시켜도 점의 개수보다 직선의 개수가 같거나 많다는 것을 보일 수 있다고 밝힌 겁니다.

다울링-윌슨 추측
2d≥p일 때 d차원 공간에 있는 점 n개가 초평면
하나에 모두 포함되지 않는다면, 그 점으로 결정
되는 (p-1)차원 공간의 수는 점 n개로 결정되는
(d-p)차원 공간의 수보다 클 수 없다.

예를 들어 d=2이고 p=1이면 이 추측은 정확하게 더브라윈-에르되시의 정리가 됩니다. d의 값은 상관없고, p=1이면 모츠킨이 해결한 문제가 되지요. 여기서 0차원 공간은 점에, 1차원 공간은 직선에 대응됩니다.

2016년 미국 고등과학원의 허준이 박사와 보통 왕 미국 위스콘신대학교 매디슨캠퍼스 교수는 다울링-윌슨 추측을 해결한 논문을 인터넷에 공개했습니다. 증명뿐 아니라 점으로 결정되는 (p-1)차원 공간을 이 점으로 결정되는 서로 다른 (d-p)차원 공간에 잘 대응시키면 앞서 말한 그린의 정리처럼 각각의 (p-1)차원 공간이 대응되는 (d-p)차원 공간에 포함되도록 대응시킬 수 있다고 밝혔지요.

이 논문은 수학 학술지 ‘악타 매스매티카’에 실릴 예정입니다. 1974년 만들어진 추측이 무려 40여 년 만에 해결된 겁니다. 이 문제를 해결하는 데는 대수기하학자도 까다로워서 잘 쓰지 않는다는 도구를 사용했습니다.

세계 수학계가 주목하는 허준이 박사

허 박사는 2014년 박사학위를 받은 새내기 수학자입니다. 하지만 조합론 분야의 오래된 미해결 문제를 대수기하학 도구를 사용해 여럿 해결하는 등 수학의 여러 분야를 연결하는 좋은 연구를 하고 있어 많은 수학자의 관심을 받고 있습니다.

허 박사는 대학에서 수학이 아닌 물리천문학을 공부했습니다. 이후 석사과정부터 수학을 본격적으로 공부했고, 석사 학위를 받은 뒤 미국으로 떠났습니다. 지도 교수도 없던 박사과정 1년차 때 조합론의 유명한 문제인 ‘리드의 추측’을 해결해 학계의 주목을 받았지요. 리드의 추측은 1968년 영국 수학자 로날드 리드가 제기한 문제입니다. 채색 다항식의 계수의 절댓값을 앞에서부터 따져봤을 때 증가하다가 감소할 수는 있지만 감소하다가 증가할 수 없다는 겁니다. 채색 다항식이란 어떤 그래프에서 이웃한 꼭짓점은 서로 다른 색이 되도록 꼭짓점을 q개 이하의 색으로 칠하는 방법의 수를 나타내는 식입니다. 예를 들어 채색 다항식 χG(q)가 q4-4q3+6q2-3q라면 1, 4, 6으로 숫자의 크기가 증가 했다가 3으로 한 번 줄어들 수 있습니다. 즉 뒤이어 나오는 계수는 절댓값이 무조건 3 이하여야 하지요.

허 박사의 첫 논문이기도 한 이 문제는 2012년 ‘미국수학회저널’에 실렸습니다. 허 박사가 앞으로도 좋은 성과를 계속 이뤄 나가길 기대해봅니다.