d라이브러리

“군부대 6곳에서 총 36명의 장교를 뽑았다. 군부대마다 소위와 중위, 대위, 소령, 중령, 대령을 한 명씩 선발한 것이다. 뽑힌 장교 36명을 가로와 세로 6줄로 세울 때, 어떤 가로와 세로 줄에서도 부대와 계급이 겹치지 않게 세울 방법이 있을까?”


스위스의 수학자 레온하르트 오일러는 1782년 위와 같은 ‘36 장교 문제’를 떠올렸어요. 고심끝에 이런 배치는 불가능하다고 추측했지요. n이 5일 때, 즉 군부대 5곳에서 계급이 다른 장교 5명씩을 뽑아 부대와 계급이 겹치지 않게 5줄씩 줄을 세우는 건 쉬워요. 하지만 6일 때는 좀처럼 답을 찾기가 어려웠어요. 이 문제는 무려 120년 동안 풀리지 않았답니다.

마침내 1901년 프랑스의 수학자 개스톤 태리가 수천 가지 경우를 일일이 따져 36 장교 문제의 답이 없다는 걸 증명했어요. 1984년에는 캐나다 수학자 더그 스틴슨, 1994년에는 미국 수학자 스티븐 도허티가 다른 증명 방법을 찾았지요. 안타깝게도 이 증명 모두 고급수학을 사용했어요. 대학생도 아는 기초 지식만을 이용한 증명법은 아직 밝혀지지 않았지요. 여러분도 36 장교 문제에 도전해 보세요!

다시 오일러의 추측으로 돌아갈게요. 오일러는 n이 6일 때뿐만 아니라 10, 14, 18처럼 n이 4k+2인 배열에서도 가로, 세로 n줄에 부대와 계급이 겹치지 않게 장교를 세울 수 없다고 추측했어요. 하지만 1959년 인도 출신 미국 수학자 라즈 찬드라 보스와 제자인 샤라드찬드라 쉬리칸데, 미국 수학자 어니스트 파커가 n이 10일 때 줄 세우는 방법을 찾으면서 오일러의 추측이 틀렸다는 게 밝혀졌지요. 이후 n이 2와 6일 때를 제외한 모든 경우에서 줄세우기가 가능하다는 것이 증명됐어요.


오일러보다 먼저 ‘직교라틴방진’ 연구한 최석정

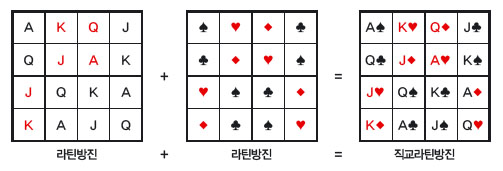
수학에서는 오일러의 추측과 같은 줄 세우기를 ‘직교라틴방진’이라고 불러요. 가로, 세로, 대각선의 합이 같도록 1부터 n까지 숫자를 적는 퍼즐을 마방진이라고 부르지요. 라틴방진은 마방진의 변형으로, 가로, 세로 줄마다 같은 숫자나 기호가 있지만 한 줄 안에서는 한 번만 나오도록 적는거예요. 마치 스도쿠처럼요. 이런 라틴방진 두 개를 하나로 합쳐 놓은 것이 직교라틴방진이에요. 다시 말해 두 라틴방진의 원소로 이뤄진 모든 순서쌍을 라틴방진의 조건에 맞게 나타낸 거예요.

직교라틴방진 연구를 ‘조합론’의 효시로 꼽기도 하는데, 유럽에서는 오일러가 1776년 직교라틴방진에 관한 논문을 써 가장 먼저 연구했어요. 그런데 최근 들어 우리나라의 최석정이 오일러보다 61년 먼저 연구했다는 사실이 밝혀졌어요. 조선시대에 영의정까지 올랐던 최석정은 1715년 ‘구수략’이라는 수학책에 9×9 배열로 이뤄진 직교라틴방진을 세계 최초로 만들어 소개했어요. 이를 이용해 9차 마방진도 만들었지요. 최석정의 연구는 자랑스러운 ‘수학 문화유산’이랍니다.

1258게임은 4차 직교라틴방진 찾기!

그런데 대체 1258게임과 직교라틴방진은 무슨 관계일까요? 눈치 빠른 독자라면 알아챘겠지만 1258게임은 1, 2, 5, 8로 이뤄진 4차 직교라틴방진의 가로와 세로에 있는 값을 찾는 게임이에요.

수학에서는 라틴방진을 n차 행렬로 표시합니다. n차 행렬이란 n×n 정사각형 안에 수나 문자를 쓴 다음 큰 괄호로 묶은 거예요. 따라서 1, 2, 5, 8을 이용해 라틴방진을 만들면 다음과 같이 행렬 A 또는 B로 나타낼 수 있어요. 이제 두 라틴방진을 합쳐야겠지요. 두 행렬의 원소가 만드는 서로 다른 순서쌍을 모두 모아 행렬로 만들면 행렬 C가 돼요.

행렬 C에서 가로 줄인 행이나 세로 줄인 열을 살펴보면 일의 자리에 1, 2, 5, 8이 한 번씩, 십의 자리에 1, 2, 5, 8이 한 번씩 나타나요. 대각선을 살펴봐도 마찬가지예요. 즉 행렬 C의 원소 각각을 두 자리 숫자 카드로 나타내면 행렬 C의 각 줄은 1258게임에서 찾아야 하는 4장의 카드가 되지요. 이제 본격적으로 1258을 즐기면서 그 속에 숨은 수학적 성질을 직접 발견해 보세요!