d라이브러리

제주는 화산활동으로 만들어진 아름다운 섬입니다. 제주 올레는 이 아름다움을 여유롭게 눈으로 즐기면서 여행할 수 있는 길입니다. 올레를 걸으며 아름다운 자연경관뿐 아니라 그 속에 숨어있는
수학을 찾아보는 여행을 시작해보려고 합니다.



‘올레’는 제주 방언으로 ‘거리에서 대문까지, 집으로 통하는 아주 좁은 골목 비슷한 길’을 뜻합니다. 옛날에는 ‘오라’ 또는 ‘오래’라고 불렀는데, 문(門)을 뜻하는 순우리말 ‘오래’가 제주에서 ‘올레’로 굳어진 것으로 보입니다.

아름다운 바다와 오름, 돌담, 곶자왈, 사시사철 푸른 들, 평화로운 마을을 품고 있는 올레는 세상에서 가장 아름답고 평화로운 길입니다. 구멍이 숭숭 난 현무암으로 이뤄져 있으며, 곳곳으로 구불구불 이어져 있습니다.

올레를 따라 걷다보면 제주도를 한 바퀴 돌 수 있습니다. 2007년 9월 8일에 시흥초등학교에서 광치기 해변에 이르는 제1코스가 개발됐고, 2012년 11월까지 총 21개 코스가 문을 열었습니다. 각 코스의 길이는 15km 이내이며, 한 코스를 걷는 데 평균 5~6시간 걸립니다.

올레는 주로 해안지역을 따라 골목길, 산길, 들길, 해안길, 오름 등으로 이어집니다. 제주도 주변에 있는 작은 섬을 체험할 수 있는 길도 있습니다. 올레를 걸으며 제주 중산간의 숨은 비경과 여러 섬의 매력을 발견해 보세요.

올레 8코스에는 수학이 있다

21가지 올레 코스에는 각각 서로 다른 특색이 있습니다. 그중 올레 8코스는 해안을 따라 작은 바닷가 마을인 안덕면 대평리로 이어지는 대표적인 바다 올레길입니다. 여미지 식물원과 테디베어 박물관이 있는 중문 관광단지를 끼고 있어 관광객 사이에 인기가 많습니다.

이 길을 걷다보면 해병대 군인들이 거친 바윗길을 평평하게 골라 해녀들이 편하게 다닐 수 있도록 만들었다는 해병대 길, 용암과 바다가 만든 주상절리도 만날 수 있습니다. 이곳에서는 자연의 수학적인 비밀을 찾아볼 수 있을 뿐만 아니라 간단하지만 신기한 수학 실험도 할 수 있습니다. 올레 8코스를 걸으며 올레 속에 숨어있는 수학을 함께 찾아볼까요?



서귀포시 중문동에 있는 관광단지 동쪽 해안가에 도착하면 시원스레 부서지는 파도 소리에 답답한 가슴이 탁 트입니다. 바다 쪽으로 가까이 가면 검붉은 육각형의 돌기둥이 병풍처럼 펼쳐져 있는 절벽을 볼 수 있습니다. 이 돌기둥은 어떻게 신이 다듬은 것처럼 정교한 육각형 모양을 하게 됐을까요?

지삿개 주상절리 알아보기

바다와 부딪치는 절벽은 대개 거대한 암석 덩어리입니다. 하지만 중문 해안가에 서 있는 이 절벽은 마치 누군가 다각형 기둥을 조각해 나란히 붙여놓은 것 같은 모양입니다. 이런 암석 구조를 ‘주상절리’라고 합니다.

절리는 온도가 약 1100℃인 용암이 화구로부터 흘러나와 빠르게 식으면서 부피가 수축한 결과 만들어집니다. 부피가 줄면서 사이사이에 틈이 생기는데, 오랜 시간 바람이 암석을 깎아 틈이 더 깊어집니다. 주상절리는 절리가 수직 기둥 모양인 경우를 말합니다. 지표면과 평행하게 자른 단면은 보통 사각형, 오각형, 육각형입니다.

중문 해안가의 주상절리는 중문동의 옛날 이름인 ‘지삿개’를 따 ‘지삿개 바위’, ‘지삿개 주상절리’라고도 부릅니다. 지삿개 주상절리는 높이가 30~40m, 폭이 약 1km 정도로 우리나라에서 최대 규모를 자랑합니다. 2004년 12월 27일에는 천연기념물 제443호로 지정돼 자연의 위대함과 절묘함을 동시에 느낄 수 있는 천혜의 자원으로 인정받기도 했지요.



지삿개 주상절리에 가장 많은 도형은?

드넓은 지삿개 주상절리에서 암석의 단면을 관찰할 구역을 정하고, 그 구역에 있는 돌기둥의 단면이 어떤 모양인지 관찰해 봅시다.

사각형, 오각형, 육각형을 볼 수 있는데 아주 짧은 선분도 놓치지 않고 세심하게 관찰해보면 육각형이 가장 많다는 것을 알 수 있습니다. 왜 그럴까요? 두 가지 활동을 통해 지삿개 주상절리에 육각형이 많이 나타나는 이유를 알아봅시다.
 
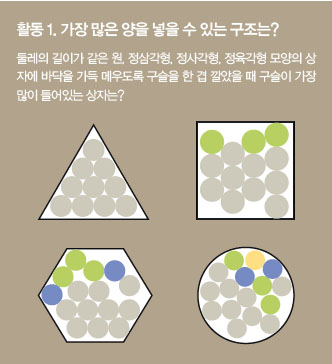
첫 번째 활동에서 원, 정육각형, 정사각형, 정삼각형 순으로 많은 구슬이 들어간다는 사실을 알아냈나요? 실험이 어렵다면 원 모양 상자에 구슬을 먼저 넣고 바닥을 평평하게 만든 다음, 구슬을 빼 육각형 상자에 넣고 같은 과정을 반복해 보세요. 정사각형, 정삼각형 모양의 상자에도 마찬가지로요. 그러면 상자별로 구슬이 얼마나 들어가는지 알 수 있습니다. 실험을 통해 가장 많은 구슬을 담기 위해서는 원 모양 상자를 선택해야 한다는 것을 알 수 있습니다.
 
하지만 원으로 평면을 가득 채우면 어떻게 될까요? 원 모양 접시를 겹치지 않도록 바닥에 늘어놓아 보세요. 그러면 접시 사이사이에 빈 공간이 생깁니다. 만약 암석 사이에 빈 공간이 있으면 암석이 안정적으로 서 있지 못할 것입니다.

반면 정육각형 모양의 색지는 바닥을 빈틈없이 덮을 수 있습니다. 내각이 120°인 정육각형 3개가 한 점을 중심으로 모여 빈틈을 만들지 않기 때문입니다. 지삿개 주상절리도 안정적으로 서 있기 위해 육각형 구조를 선택하지 않았을까요?




주상절리를 지나 다음 목적지까지 얼마나 남았을까요? 얼마나 걸었는지 잴 수 있는 도구가 없을 때 대략적으로 우리가 걸어온 거리, 앞으로 남은 거리를 구하고 싶다면 보폭을 이용하면 됩니다.

보폭으로 거리 재기

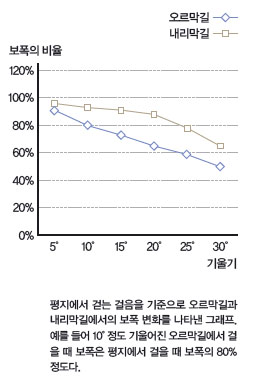
앞발 뒤축에서 뒷발 뒤축까지의 거리, 즉 ‘보폭’으로 거리를 재는 방법을 ‘보측’이라고 합니다. 거리를 알고 싶은 두 지점 사이를 걸어 보고, 걸음 수에 자신의 평균 보폭을 곱하면 됩니다.

평균 보폭을 곱하는 이유는 우리가 항상 똑같은 보폭으로 걷지 않기 때문입니다. 그래서 일정한 거리를 몇 번씩 걸어본 다음 평균을 구하는 방법을 씁니다. 예를 들어 100m를 평균 154걸음 안에 걸었을 경우 평균 보폭은 100m÷154=0.65m, 즉 65cm가 됩니다.

지삿개 주상절리를 나와 씨에스 호텔로 가던 중 일정 구간의 거리를 재봤습니다. 먼저 100cm 줄자를 바닥에 붙여놓고 줄자 위를 여러 번 걸어 보폭을 잰 다음 계산기로 평균 보폭을 구했습니다. 그리고 거리를 잴 구간의 끝 지점까지 몇 걸음을 걸었는지 각자 세 보는 겁니다. 보폭이 작은 친구는 끝 지점까지 걸음 수가 많고 보폭이 큰 친구는 걸음 수가 적었지요. 그 다음 총 거리를 계산하기 위해 각자 걸음 수와 자신의 평균 보폭을 곱했습니다.

그런데 구간의 거리를 잰 값은 사람마다 큰 차이를 보였습니다. 아마 거리를 재야겠다고 생각하면서 걷는 바람에 자신이 측정한 평균 보폭보다 크게 또는 작게 걸었을 겁니다. 걸음 수를 세다가 놓친 친구도 있을 겁니다. 만약 충분히 먼 거리를 걸었다면 어느 순간 자연스럽게 걷게 돼 오차가 줄었을 겁니다. 걸음 수를 재는 만보기를 들고 걷는다면 걸음 수를 빼놓지 않고 셀 수 있으니 더 정확하게 거리를 잴 수 있을 겁니다.