d라이브러리

올해 중국에서 열리는 광저우아시안게임에서 바둑은 처음으로 정식종목이 됐다. 금메달이 3개나 걸려 바둑이 또 하나의 스포츠로 인정받은 셈이다. 이 글에서는 바둑을 전혀 모르는 사람도 바둑을 쉽게 이해할 수 있는 원리를 설명하고자 한다. 바둑돌을 전기를 띤 알갱이로 비유하는 방식으로 말이다. 평소 생각을 정리한 것이지만 필자의 바둑 실력이 아마추어 3, 4단밖에 안 돼 기고를 망설여왔다. 하지만 수치적 결과들이 재미있고 명쾌해 감히 소개해 보기로 한다.


우주를 담은 스포츠, 바둑

바둑판은 가로세로가 똑같이 19줄로 총 19×19=361집을 갖는다. 한가운데 있는 ‘천원’이라는 점을 제외하면 모두 360집이 되는데, 이는 1년이 약 360일이라는 천문학적 사실에서 비롯한 것이다. 흑과 백이 어우러지는 바둑은 음양오행 이론에 기반을 두고 우주를 형상화한 스포츠다. 그래서 ‘신선놀음’ 또는 ‘선비놀음’ 하면 가장 먼저 떠오르는 것 역시 바둑이다. 서양의 체스가 동양의 장기에 해당한다고 볼 때, 서양에는 동양의 바둑에 해당하는 스포츠가 없다. 이 사실만 봐도 우주에 대한 동양의 애착이 서양보다 더 깊다고 한다면 과언일까?

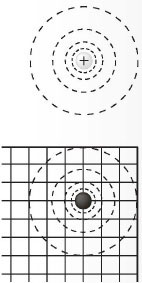
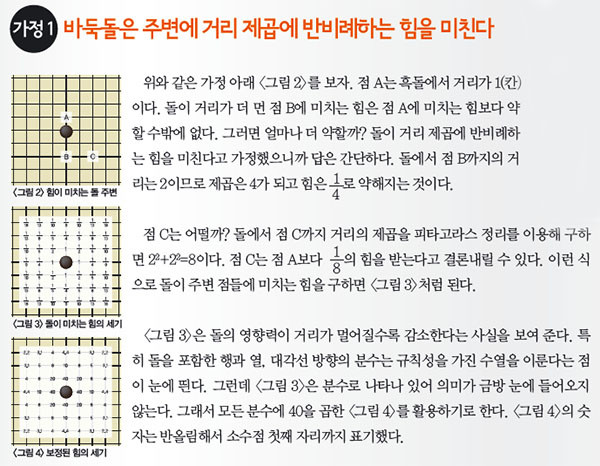
심오한 바둑의 원리를 수치적으로 설명하기 위해 이 글에서는 바둑돌을 전기장을 형성하는 전하에 비유하고자 한다. 즉 <;그림 1>;처럼 주변에 거리 제곱에 반비례하는 전기력을 미치는 *전하와 바둑돌을 동일시하겠다는 뜻이다. 바둑을 전혀 모르는 사람도 이 글을 읽는 데 지장이 없을 것으로 믿는다.
 

가정2 여러 바둑돌이 미치는 힘은 숫자의 합으로 구한다
 

두 번째 가정은 계산을 최대한 단순하게 만들기 위해서 도입했다. 필자는 계산기를 쓰지 않고, 심지어 지루한 국제선 비행기 안에서도 손으로만 계산해 이 원고를 작성했다. 힘의 세기는 단순한 숫자의 합이 아니라 방향도 같이 고려해야 한다. 하지만 방향의 합은 계산기를 쓰지 않고는 구할 수 없을 뿐 아니라 값이 크게 다르지 않으므로 이 가정을 받아들이기로 한다.
 

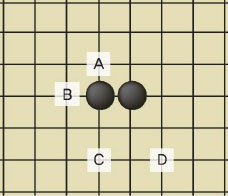
두 바둑돌이 나란히 놓인 <;그림 5>;를 보자. 두 돌이 점 A에 미치는 힘은 어떻게 구할까? <;그림 4>;에서 왼쪽 돌이 점 A에 미치는 영향은 40, 오른쪽 돌이 미치는 영향은 20임을 알 수 있다. 따라서 가정 2에 따라 두 돌이 점 A에 미치는 힘의 세기는 40+20=60이 된다.
 

마찬가지로 두 돌이 점 B에 미치는 힘은 40+10=50, 점 C에는 10+8=18, 점 D에는 5+8=13이 된다. 이런 식으로 나란히 놓인 두 돌 주변의 힘의 세기를 구하면 <;그림 6>;과 같이 된다.
 

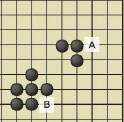
이번에는 <;그림 6>;의 경우보다 두 돌의 간격을 더 넓힌 <;그림 7>;과 <;그림 8>;의 경우를 보자. 주어진 숫자의 크기를 보더라도 <;그림 7>;의 경우가 <;그림 6>;이나 <;그림 8>;의 경우보다 더‘효율적’임을 알 수 있다. 효율적이란 말은 두 돌이 미치는 힘이 더욱 넓고 크게 퍼져나갈 수 있다는 뜻이다. 여기서 <;그림 7>;의 두 돌 간격이 적당하다는 사실을 깨닫게 된다. 실제 바둑에서도 <;그림 6>;이나 <;그림8>;처럼 두 돌을 놓는 경우는 흔치 않다. 마찬가지 원리로 <;그림 9>;의 A와 같은 ‘빈삼각’ 모양이나 B와 같은 ‘포도송이’ 모양을 피하는 이유도 잘 설명된다.
 

가정3 흑과 백은 서로의 힘을 소멸시킨다
 

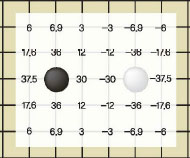
바둑은 둘이 두는 스포츠다. 따라서 흑이 놓으면 다음은 백의 차례가 된다. 흑의 돌이 <;그림 4>;처럼 어딘가에 놓여 바둑판 전체에 힘을 미치고 있다고 하자. 백은 어디에 둬야 할까? 백돌도 <;그림 4>;처럼 주변에 힘을 미쳐야 하지만 가정 3에 따라 우리는 백돌이 미치는 힘에 (-) 부호를 붙이기로 한다. 즉 <;그림 10>;처럼 흑돌이 주변에 (+) 값의 숫자로 힘을 미친다면 백돌은 (-) 값의 숫자로 흑돌의 힘을 상쇄시키는 것이다.
 

이 가정을 도입하면 원리적으로는 바둑 소프트웨어를 만들 수 있다. 흑이 첫 수를 두면 바둑판에서 돌이 놓인 점을 제외한 나머지 360점에 미치는 힘의 크기를 모두 (+) 숫자로 부여한다. 다음으로 백이 두면 359점에 (-) 숫자를 부여해 흑돌이 부여했던 (+) 숫자들을 상쇄시키는 것이다. 즉 백이 놓아야 할 곳은 흑의 힘을 최대한 상쇄시키는 점이 된다. 물론 처음에는 답이 여러 개 나오겠지만 경기를 진행할수록 개수는 줄어들 것이다.

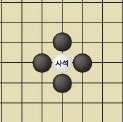
가정 3은 <;그림 11>;처럼 사석, 즉 죽은 돌을 정의하는 데도 자연스럽다. 즉 사방이 막혀 힘을 잃은 돌을 죽었다고 정의하는 것이다.
 

바둑에서는 한 점을 들어낸 모양을 ‘빵때림’ 했다고 표현한다. ‘빵때림 30집’이라는 말이 있듯이 빵때림의 위세는 대단하다. <;그림 4>;처럼 숫자로 표현하면 빵때림의 위세는 <;그림 12>;에서 보는 바와 같다.
 

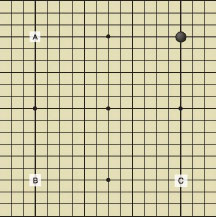
문제는 계산대로라면 흑이 첫 수를 무조건 바둑판의 한가운데인 *‘천원’에 둘 수 밖에 없다는 점이다. 그래야만 백이 다음 수를 어디에 두더라도 (+)값이 남기 때문이다. 이것만 보더라도 먼저 두면 유리하다는 사실을 깨닫게 된다. 하지만 실제 바둑에서는 바둑판의 가운데보다는 *‘변’에, 변보다는 *‘귀’에 먼저 돌을 놓는다. 예를 들어 바둑 초반, 즉 포석단계에서는 <;그림 13>;에서 보는 바와 같이 첫 수를 흑이 *‘화점’에 두고 백은 다른 화점 A, B, C 주위 어딘가에 두게 된다.
 

이뿐 아니다. 포석단계에서 <;그림 14>;에서 보는 바와 같이 가장자리로부터 5번째 줄부터 중앙 방향으로는 돌을 놓지 않는다. 따라서 우리는 귀와 변에 가산점을 부여할 수밖에 없다. 그리고 변보다는 귀가 가산점이 더 커야 한다.

가정4 바둑판의 가장자리는 힘을 반사하는 '거울'이다
 

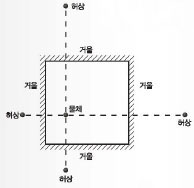
문제는 귀와 변에 어떻게 가산점을 주느냐에 있다. 필자는 그 방법의 하나로 바둑판의 가장자리를 거울로 가정하는 아이디어를 제시하고자 한다. <;그림 15>;에서 보는 바와 같이 사방이 거울로 둘러싸인 한 점에 물체가 놓이게 되면 물체 하나에 4개의 *‘허상’이 맺힌다. 이것을 바둑판에 적용해 보자.

필자의 생각은 바둑돌의 허상 4개의 힘을 합해 주자는 것이다. 이를 고려하면 <;그림 16>;에서 보는 바와 같이 힘의 크기가 마치 거울에 반사해 보태지는 것처럼 자연스러워진다.
 

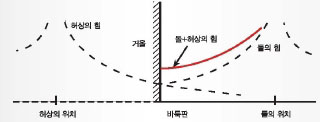
그뿐 아니라 돌이 귀에 가까이 놓일수록 허상 2개가 더욱 접근하므로 귀는 자연스럽게 변보다 더욱 큰 값을 갖게 된다. <;그림 15>;에서는 바둑판을 위에서 내려다 보는 것이고 <;그림 16>;에서는 바둑판을 옆에서 보는 것임에 유의하자.
 

이런 식으로 돌이 ‘33’에 놓인 경우를 <;그림 4>;처럼 나타내면 <;그림 17>;이 된다. 비교하면 값이 분명하게 보정됐음을 알 수 있다.

이제 사람이 먼저 흑을 두고 컴퓨터가 백을 두는 소프트웨어를 생각해 보자.
 

더욱 정확한 소프트웨어를 만들려면 가정 2를 버리고 방향의 합을 함께 고려하는 방식으로 바꿔야 할 것이다. 하지만 근본적으로 바둑돌의 힘이 거리에 따라 얼마나 달라지는지 소프트웨어를 만들어 돌려보기 전에는 알 길이 없다. 또한 거울의 반사율도 문제가 될 것이다. 일단 완성된 소프트웨어가 바둑을 두는 정석들을 잘 구현하는지 여부에 따라 미세하게 조정해야 할 것이다.

위대한 바둑 9단

프로 바둑기사가 아무리 잘 해도 9단이 끝이다. 여러 가지 이유가 있겠지만, 동양에서 하늘을 9개로 나누는 ‘9천사상’ 때문이다. 워낙 9라는 숫자를 받들다 보니 봉우리가 많은 산은 죄다 ‘9봉산’이라고 이름을 지어 우리나라에 9봉산이 몇 개나 있는지 모른다. 이처럼 ‘9단’은 위대한 것이다.

* 전하: 물체가 띠고 있는 정전기의 양, 양전하와 음전하로 나뉜다.
*귀, 변, 화점, 천원 : 바둑판의 네 귀퉁이 부분을 ‘귀’라 하고, 귀와 귀 사이의 가장자리 부분을 ‘변’이라고 한다. 따로 표시된 9개의 점을 ‘화점’이라고 하는데 특히 중앙의 것을 ‘천원’이라고 한다.
*허상 : 빛이 거울에 반사될 때, 그 반사되는 방향과 반대의 방향으로 연장한 곳에 맺히는 가상적인 상.