
인생은 선택의 연속입니다. 살다보면 우리는 항상 갈림길 위에 서 있습니다. 어떤 길을 가는지에 따라 해피엔딩을 맞을 수도 있고 비극의 주인공이 되기도 합니다. 하지만 누구도 그 결말을 미리 알진 못합니다. 그렇다고 마구잡이로 선택하고 모든 걸 운에 맡길 수는 없습니다. 그래서 확률이 필요합니다. 확률이 앞날을 100% 맞히지는 않지만, 최소한 어떤 ‘가능성’이 있는지 말해 줍니다. 만약 어떤 길이 무너질 확률이 70%라면, 그 길을 피해서 가는 편이 좋습니다. 험난한 미래를 확률로 내다보기 위해선, 먼저 어떤 길이 있는지부터 모두 파악해야 합니다.
경우를 알아야지!
주사위를 굴리면, 1에서 6까지 모두 여섯 가지 경우가 나옵니다. 이렇게 일어날 수 있는 모든 사건의 수를 ‘경우의 수’라고 합니다. 확률 계산은 경우의 수를 구하는 일부터 시작합니다. 주사위를 굴려 짝수가 나오는 경우의 수는 3가지(2,4,6)입니다. 따라서 주사위 게임에서 짝수가 나올 확률은 3(짝수가 나오는 경우의 수)/6(모든 경우의 수), 즉 50%죠. 주사위가 2개가 되면 어떨까요? 이젠 손가락만으로는 벅찹니다. 도구가 필요하죠.
이항정리는 경우의 수를 구하는 가장 기초적인 도구입니다. 이항정리는 두 항의 합을 거듭제곱한 결과를 나타내는 공식입니다. 예를 들어, (a+b)를 제곱하면 a²+2ab+b²이 나옵니다. 이항정리를 이용하면 그 이유를 알 수 있습니다.
a와 b가 하나씩 들어 있는 주머니 두 개를 떠올려 봅시다. a+b를 제곱한다는 건, 두 주머니에서 a와 b를 하나씩 뽑아서 곱한 뒤 더하는 일과 마찬가지입니다. a²은 두 주머니에서 모두 a를 뽑으면 됩니다. ab는 주머니 중 한 곳에서만 a를 꺼내는 경우죠. b²은 b를 2개 꺼내는 경우지만, a를 0개 뽑는다고 생각해도 똑같습니다. 이항정리를 사용하면 다음같이 정리할 수 있죠.
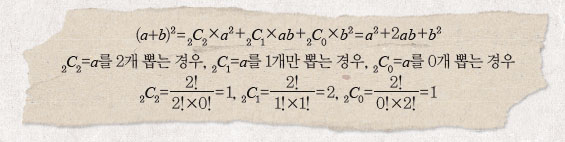
C는 조합을 뜻하는 영어단어 ‘combination(콤비네이션)’의 약자입니다. 수학에서 조합이란 여러 개 가운데에서 몇 개를 순서에 관계없이 뽑는 경우를 뜻합니다. nCr은 서로 다른 n개에서 r개를 순서에 상관없이 뽑는 가짓수를 말합니다. *계산도 어렵지 않습니다. 이항정리를 이용하면 복잡한 거듭제곱도 쉽게 구할 수 있습니다. 가능한 a×b의 꼴을 모두 적어 놓고, 조합 공식으로 각 경우에 맞는 수를 구해 써주기만 하면 됩니다.
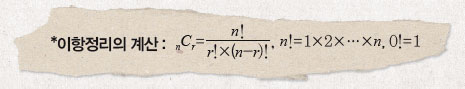
이항정리로 미래를 엿본다
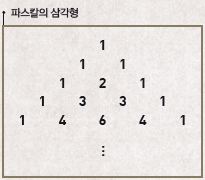
이항정리를 이용하면 아름다운 삼각형을 만들 수 있습니다. 바로 파스칼의 삼각형입니다. 파스칼의 삼각형은 이항계수(nCr)를 순서대로 늘어놓은 삼각형 꼴의 모형을 말합니다. 단순하게 생겼지만 그 수학적 의미는 결코 가볍지 않습니다.
자연수의 수열에서 피보나치의 수열까지 다양한 수열이 파스칼의 삼각형 속에 숨어 있습니다. 삼각형의 가로 방향의 합은 항상 2의 거듭제곱입니다. 서로 다른 n개를 조합하는 모든 경우를 더하면 2ⁿ개라는 뜻입니다. 삼각형의 대각선 방향의 합은 마지막 수의 반대 방향 아래에 있는 수와 같습니다. 짝수와 홀수 자리마다 서로 다른 색을 칠하면 신비로운 프랙탈 무늬가 나타납니다.
파스칼의 삼각형을 유리수 영역으로 확장하면 더욱 흥미로운 결과가 나옵니다. 확률이 정확히 1/2인 동전 던지기를 이항정리로 정리하면 종모양의 그래프를 얻을 수 있습니다. 단위를 조금만 맞춰 주면, 이 곡선은 통계학의 뿌리를 이루는 정규분포가 됩니다.
정규분포는 값이 평균 근처에 모여 있고, 평균을 중심으로 양쪽으로 대칭인 종 모양의 확률분포를 말합니다. 정규분포를 보면 왜 세상에 중간이 많은지 알 수 있습니다. 어떤 종류의 시험이든 0점이나 100점보단 60점이나 70점이 많죠. 성적이 정규분포를 따르기 때문입니다. 키와 몸무게에서 수면 시간과 식사 시간까지 우리 주변의 많은 현상이 정규분포를 따릅니다. 여론조사를 할 때도 자료를 정규분포로 분석합니다. 이항정리를 이해하면 앞날까지 내다 볼 수 있는 셈이죠.
이항정리의 저작권은 누구에게?
파스칼의 삼각형이라는 이름 때문인지, 파스칼이 처음 발견한 것 같지만 이항정리는 아주 오래 전부터 알려져 있던 사실입니다. 이미 기원전 400년 무렵 그리스의 유클리드가 (a+b)²에 대한 이항정리를 언급한 기록이 있습니다. 그로부터 100년 뒤 인도의 수학자 핑갈라는 더욱 높은 차수의 이항정리까지 풀어 놓았습니다.
삼각형 모양의 전개식도 파스칼이 태어나기 훨씬 전부터 있었습니다. 송나라 수학자 양휘는 이항정리의 개념을 파스칼의 삼각형과 거의 비슷한 모양으로 설명했습니다. 11세기 페르시아의 수학자 오마르 카이얌도 임의의 정수 n에 대한 이항정리를 제시해 놓았습니다. 이항정리의 저작권은 인류의 역사가 갖고 있다고 해도 지나치지 않습니다.
조합의 맛, 커리
우리가 즐겨 먹는 카레는 걸쭉한 소스 형태지만, 카레의 할아버지뻘인 인도의 커리는 묽은 국물에 가깝습니다. 끈적한 커리, 카레의 고향은 일본입니다. 19세기말 일본은 영국의 모든 걸 닮고 싶어 했습니다. 영국 사람이 즐겨 먹는 커리도 마찬가지였죠. 그런데 묽은 커리는 일본사람이 주로 먹는 밥과 어울리지 않았습니다. 한 요리사가 묽은 커리에 밀가루를 섞어 끈적하게 만들자는 생각을 합니다. 결과는 대성공이었죠. 끈끈해진 카레는 찰기 있는 밥알과 찰떡궁합을 이룹니다. 우리나라도 일본의 영향으로, 커리보다 일본식 카레를 즐겨 먹게 됐습니다.
인도에서 커리란 카레처럼 특정한 소스가 아니라, 갖은 재료에 수많은 향신료를 섞어 만든 국물 있는 요리를 의미합니다. 인도는 어느 나라보다 향신료 문화가 발달했습니다. 더운 기후에 향신료를 쓰지 않으면, 음식이 쉽게 상하기 때문이죠. 처음엔 음식을 오래 먹기 위해 향신료를 썼지만, 인도사람들은 점점 향신료만의 독특한 맛에 빠져들었습니다. 시간이 흘러 이슬람의 음식문화까지 전해지면서, 인도는 ‘향신료의 천국’이 됩니다. 오죽하면 영국이 인도를 침략한 이유가 ‘양념’ 때문이라는 농담이 있을 정도죠.
커리의 맛은 향신료를 어떻게 섞는지에 따라 정해집니다. ‘향신료의 조합’이 커리 맛의 비결인 겁니다. 인도에서는 다양한 향신료를 섞어 만든 혼합양념을 ‘마실라’라고 부릅니다. 마실라는 정해진 형태가 없습니다. 자신이 원하는 향신료를 알아서 섞어 만들면 됩니다. 계피, 육두구, 정향, 강황, 후추, 소금, 고추…. 차마 이 글에 다 적을 수 없을 만큼 인도의 향신료는 무궁무진합니다. 그만큼 그 조합인 마실라의 종류도 셀 수가 없죠.
당연히 커리의 종류도 상상 이상으로 다양합니다. 인도인이 커리의 종류가 자신들의 인구(13억)만큼 있다고 하는 건 결코 허풍이 아닙니다. 매일 먹는 카레가 아니라, ‘조합의 맛’ 인도식 커리에 도전해 보는 건 어떨까요?











