d라이브러리

※ 편집자 주
2018년 8월 1일 열리는 브라질 리우데자네이루 세계수학자대회 개막식에서 만 40세 미만의 젊은 수학자가 받을 수 있는 최고 영예, 필즈상 수상자가 정해 집니다. 올해는 누가 수상의 영광을 누리게 될까요? 7개월간 필즈상 후보자 10명을 뽑아 소개합니다.

아홉 번째 필즈상 후보는 브라질 수학자 페르난도 코다 마르케스 교수입니다. 2014년 서울 세계 수학자대회의 기조강연자로, ‘윌모어의 추측’이라는 미분기하학의 유명한 난제를 풀어 수학계 눈도장을 확실히 찍은 수학자입니다.

하지만 마르케스 교수가 처음부터 수학을 공부했던 건 아닙니다. 대학교 학부 전공은 토목공학인데, 대학 때 수학에 매료돼 수학자로 진로를 바꿨습니다. 아주 어릴 때부터 수학을 좋아했지만 수학자가 어떤 일을 하는지 몰라서 수학자를 꿈 꿔 본 적은 없다고 합니다. 그래서 브라질 학생들에게 수학자가 어떤 일을 하는지 제대로 알려주고 싶다고 언론 인터뷰를 통해 밝히기도 했습니다.

마르케스 교수의 대표 업적은 앞서 이야기한 윌모어의 추측입니다. 1965년 영국 수학자 톰 윌모어는 유클리드 공간이 어떤 모습일 때 가장 효율적으로 휘어있는지, 즉 다양체가 어떤 모양일 때 곡률(휘어 있는 정도)이 가장 작은지에 관해 관심을 가졌습니다. 그리고 다양체의 각 점의 평균 곡률을 제곱해 다 더한 함수식인 ‘윌모어 에너지’를 통해 그 다양체를 알아내려고 했지요.

윌모어는 도넛 모양의 원환면과 위상동형인 다양체 중에서 윌모어 에너지가 최소인 것, 즉 가장 효율적으로 휘어진 것을 찾아 나섰습니다. 하지만 계산이 너무 복잡하고 어려워서 모든 경우를 알아보기가 힘들었고, 결국 울퉁불퉁하게 생긴 모양은 제외하고 원환면의 두께가 뚱뚱한 것과 날씬한 것만 살펴봤지요.

그 결과 윌모어 에너지가 2π2인 원환면이 가장 효율적으로 휘어져 있다는 걸 알아냈습니다. 그리고 울퉁불퉁하게 생긴 모양까지 다 포함해도 이 윌모어 에너지가 최소일거라고 추측했지요.

미분기하학 난제, 새 관점으로 해결

2012년 마르케스 교수는 안드레 네베스 영국 임페리얼 칼리지 런던 교수와 함께 ‘스테레오 투영법’을 써서 이 문제를 재해석해 윌모어의 추측이 참이라는 걸 밝힙니다. 스테레오 투영법이란 평면 위의 모든 점을 구면에 일대일 대응시키는 방법입니다. 이 방법을 쓰면 3차원 유클리드 공간의 문제를 3차원 초구, 즉 2차원 곡면인 속이 빈 구를 3차원으로 확장시킨 공간의 문제로 바꿀 수 있습니다.

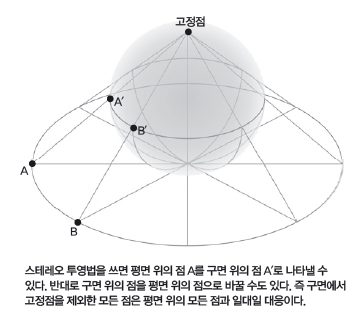
같은 분야를 연구하고 있는 서검교 숙명여자대학교 교수는 “윌모어는 아주 특별한 경우에만 최솟값이 2π2이라는 걸 알았다”면서, “스테레오 투영법이라는 아이디어로 공간을 바꿔 미분기하학의 난제를 푼 것”이라고 설명했습니다.

한편 마르케스 교수 하면 ‘의리’를 빼놓을 수 없습니다. 지도교수가 암에 걸려 박사학위를 받기 전에 세상을 떠날지도 모르는 시한부 선고를 받았음에도 불구하고 끝까지 지도교수 옆에서 연구를 이어갔기 때문입니다. 뛰어난 연구 성과로 미국 코넬대학교 대학원생이 받을 수 있는 최고 영예인 베티그상도 수상하고, 무사히 박사 학위도 받았습니다.

올해 세계수학자대회는 브라질에서 열립니다. 운동선수는 자국에서 하는 대회에서 메달을 딸 때 더 뜻깊게 생각하죠? 수학자도 예외는 아닐겁니다. 역사상 자국에서 필즈상을 받은 수학자는 단 4명뿐입니다. 마르케스 교수도 그 대열에 합류할 수 있을까요? 8월 1일에 그 결과를 지켜봐 주세요.