크루아상을 만드는 모습은 예술에 가깝다. 보따리 싸듯이 버터를 소중하게 감싼 반죽을 여러 번 밀고 접어 층을 내고, 편평해진 반죽을 지그재그로 자른다. 이등변삼각형으로 자른 반죽을 넓은 부분부터 좁은 부분까지 돌돌 말아 오븐에 구우면 ‘맛있는 초승달’이 탄생한다.

완성된 크루아상을 반으로 잘라보면 커다란 구멍이 숭숭 뚫려 있다. 이스트가 밀가루 반죽을 발효시키면서 이산화탄소를 내뿜은 증거다. 공기가 빠져나가면서 빵이 주저앉지 않고, 예쁘게 부풀어 오를 수 있는 건 반죽 안에 글루텐이 생겼기 때문이다. 게다가 크루아상이 숨기고 있는 쫄깃하고 하얀 속살도 글루텐 덕분이다.
글루텐은 밀가루에 물을 붓고 반죽할 때 생기는 그물구조다. 밀가루 단백질 중 반죽을 끈적이고 탄탄하게 하는 글루테닌과 잘 늘어나게 하는 글리아딘이 사슬모양으로 재결합한 것이다. 글루텐이 많으면 쫄깃하고 부드러운 빵이 되고, 글루텐이 적으면 바삭바삭하게 부서지는 과자가 된다. 크루아상의 안쪽은 식빵처럼 쫄깃하지만 표면은 쿠키처럼 부서져야 제맛이다. 글루텐이 많은 강력분으로만 만들면 표면이 질겨지고, 글루텐이 적은 박력분으로만 만들면 안쪽까지 바삭바삭해진다. 크루아상을 만들 때는 식빵을 만들 때의 60% 정도만 글루텐을 만들면 된다. 그래서 강력분과 박력분을 섞어서 반죽한다.
그렇다면 강력분과 박력분을 얼마나 섞어야 제대로 된 크루아상을 만들 수 있을까? 프랑스빵을 과학적으로 연구하는 캐나다의 제빵연구가 베리 파라는 밀가루 반죽이 쫄깃한 정도와 쭉 늘어나는 정도를 계산하는 식을 만들어 답을 찾아냈다. 밀가루 단백질 중 글루테닌은 반죽의 탄성★을, 글리아딘은 점성★을 결정하기 때문에 그 비율을 계산하면 알 수 있다는 것이다. 글루테닌 양과 글리아딘 양의 비율은 글루텐의 두께(P)와 길이(L)의 비로 알 수 있다.
[탄성★ 반죽을 늘이거나 비틀었을 때 원래 모습대로 되돌아오려는 성질.
점성★ 반죽이 길게 늘어나는 성질.]
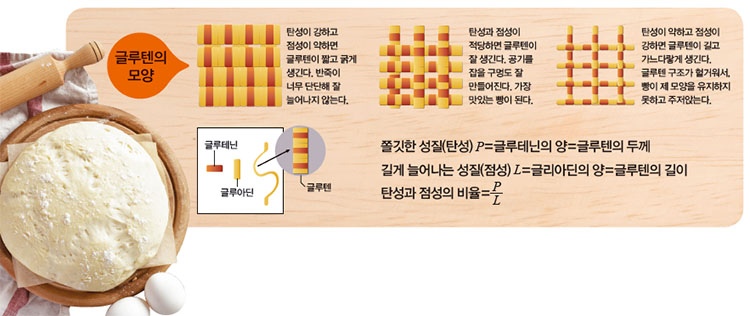

식빵이나 소보루빵처럼 푹신푹신한 빵을 만들 때는 P/L의 값이 0.6에서 0.68 사이가 되는 것이 좋다. 글루텐의 탄성과 점성이 좋아 반죽이 부풀면서 생기는 이산화탄소를 붙들 만큼 적당한 크기로 구멍이 뚫리기 때문이다. 만약 P/L가 0.5보다 작으면 점성이 강하기 때문에 반죽이 늘어진다. 이산화탄소를 붙들지 못해 반죽이 잘 부풀지 않는다. P/L가 0.68보다 크고 0.9에 가까우면 탄성이 강하고 점성이 약해 구멍이 크게 뚫린다. 이 경우 이산화탄소가 구멍으로 다 새어나가 반죽이 주저앉아 버린다.
하지만 일반 빵과 달리 크루아상은 점성이 커야 한다. P/L의 값이 0.42 정도면 적당하다. 여러 번 접어 층을 겹겹이 만들려면 반죽이 쭉쭉 늘어나야 하기 때문이다. 수학자들은 실험을 통해 강력분과 박력분을 3:1의 비율로 섞어 반죽하면 맛있는 크루아상을 만들 수 있다는 것을 알아냈다.

크루아상의 표면이 바삭바삭하게 바스러질 수 있는 것은 빵이 종이보다 얇게 켜켜이 여러 층으로 되어 있기 때문이다. 손가락으로 잡아 살짝 당겨보면 한 층 한 층 벗겨진다. 어떻게 층마다 엉겨 붙지 않고 나눠져 있는 걸까? 그건 층과 층 사이에 얇은 버터 층이 있기 때문이다. 크루아상은 버터 층이 생명이기 때문에 버터가 녹지 않도록 차가운 밀가루에 차가운 우유를 붓고 서늘한 곳에서 반죽한다.
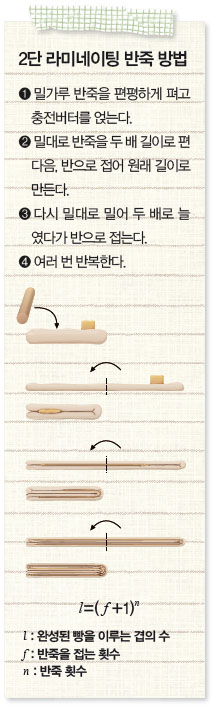
밀가루 층 사이사이에 얇은 버터 층을 만드는 비결은 바로 ‘라미네이팅 반죽’이다. 발효를 마친 반죽을 편평하게 민 다음 적당히 접어 정사각형을 만든다. 반죽 위에 충전버터★를 올려놓고 3등분을 한 듯이 양 옆을 접어 덮는다. 그 다음 밀대로 밀어 처음 길이만큼 반죽을 늘이고, 다시 양 옆을 접는다. 이것을 여러 번 반복하면 버터가 반죽 사이사이에 들어간다. 제빵사가 얼마나 반죽을 접었느냐에 따라 크루아상 겹의 수가 73~730장 정도 된다. 크루아상이 총 몇 겹으로 돼 있는지는 반죽을 접는 횟수를 알면 구할 수 있다.
라미네이팅 반죽을 하면 양옆을 포개서 접기 때문에 한 번 반죽했을 때 3겹, 두 번 했을 때 9겹, 세 번 했을 때 27겹, 네 번 했을 때 81겹이 된다.
그런데 이렇게 반죽을 접기만 해도 버터가 골고루 섞일 수 있을까? 수학자들은 크루아상을 만들 때 하는 3단 접기보다 단순한 2단 접기만으로도 버터가 충분히 골고루 섞인다는 것을 알아냈다. 수학자들은 2차원 평면에 놓인, 한 변의 길이가 1인 정사각형 모양의 반죽을 생각했다. 그리고 버터 한 조각을 반죽 위에 올려놨다. 반죽을 밀고, 접는 과정에서 버터가 어디로 이동하는지 알기 위해서다. x는 정사각형의 밑변에서 수직으로 잰 버터의 높이다.
그리고 반죽을 밀어 길이가 두 배가 되도록 한 뒤 반으로 접어 원래 길이로 만드는 과정을 반복했다. 이때 버터가 퍼지지 않도록 버터의 아랫부분에 있는 반죽을 위쪽으로 밀었다. 그 결과 한 번 반죽을 밀고 반으로 접었을 때, 처음 버터의 높이 x가 어떻게 바뀌는지를 식으로 나타낼 수 있었다(f(x)는 버터의 나중 높이).
밀가루 층 사이사이에 얇은 버터 층을 만드는 비결은 바로 ‘라미네이팅 반죽’이다. 발효를 마친 반죽을 편평하게 민 다음 적당히 접어 정사각형을 만든다. 반죽 위에 충전버터★를 올려놓고 3등분을 한 듯이 양 옆을 접어 덮는다. 그 다음 밀대로 밀어 처음 길이만큼 반죽을 늘이고, 다시 양 옆을 접는다. 이것을 여러 번 반복하면 버터가 반죽 사이사이에 들어간다. 제빵사가 얼마나 반죽을 접었느냐에 따라 크루아상 겹의 수가 73~730장 정도 된다. 크루아상이 총 몇 겹으로 돼 있는지는 반죽을 접는 횟수를 알면 구할 수 있다.
라미네이팅 반죽을 하면 양옆을 포개서 접기 때문에 한 번 반죽했을 때 3겹, 두 번 했을 때 9겹, 세 번 했을 때 27겹, 네 번 했을 때 81겹이 된다.
그런데 이렇게 반죽을 접기만 해도 버터가 골고루 섞일 수 있을까? 수학자들은 크루아상을 만들 때 하는 3단 접기보다 단순한 2단 접기만으로도 버터가 충분히 골고루 섞인다는 것을 알아냈다. 수학자들은 2차원 평면에 놓인, 한 변의 길이가 1인 정사각형 모양의 반죽을 생각했다. 그리고 버터 한 조각을 반죽 위에 올려놨다. 반죽을 밀고, 접는 과정에서 버터가 어디로 이동하는지 알기 위해서다. x는 정사각형의 밑변에서 수직으로 잰 버터의 높이다.
그리고 반죽을 밀어 길이가 두 배가 되도록 한 뒤 반으로 접어 원래 길이로 만드는 과정을 반복했다. 이때 버터가 퍼지지 않도록 버터의 아랫부분에 있는 반죽을 위쪽으로 밀었다. 그 결과 한 번 반죽을 밀고 반으로 접었을 때, 처음 버터의 높이 x가 어떻게 바뀌는지를 식으로 나타낼 수 있었다(f(x)는 버터의 나중 높이).

아무리 늘여도 반죽은 2를 넘지 않고, 2가 되면 다시 반으로 접어 1이 된다. 이를 여러 번 되풀이하면 버터 입자들이 아주 멀어지면서 반죽에 골고루 섞인다. 결국 애써 마구잡이로 주무르지 않고 단순한 동작을 반복하는 것만으로도 버터는 반죽에 골고루 섞인다는 뜻이다.
크루아상은 17세기 말, 헝가리에서 통통한 초승달 모양의 발효빵으로 탄생했다. 그 후 헝가리에서 오스트리아로 전해지고, 오스트리아의 공주였던 마리 앙투아네트가 루이 16세와 결혼하면서 1774년에 프랑스로 전해졌다. 지금처럼 수많은 겹을 가진 크루아상은 1920년대 초 프랑스 제빵사들이 만들었다. 버터를 고루고루 섞어 질감이 더욱 다양해지고 풍미가 훨씬 진한 빵을 만들려는 노력에서 비롯된 것이다. 우리나라에서는 팥이나 잼, 인절미 등을 품고 붕어빵으로 태어난 크루아상이 앞으로는 어떤 모습으로 재탄생할까? 크루아상의 맛있는 변신이 기대된다.
[충전버터★ 페이스트리를 만들 때 반죽 안에 채워 넣는 버터. ‘롤인버터’라고도 부른다.]