
전쟁과 환경오염으로 지구가 걷잡을 수 없이 망가진 2115년 지금, ‘화성 이주’는 더 이상 상상이 아니다. 운명이다. 인류에게 남은 선택지는 화성뿐이다. 무작정 간다고 살 수는 없다. 인간답게 살기 위해선, 기본부터 갖춰야 한다. 해답은 수학 속에 있다.
Part 1 새로운 문명의 출발
천리길은 시뮬레이션부터
화성으로 이주한다는 건 옆 동네로 이사가는 일과는 차원이 다른 문제다. 무작정 떠났다간 우주미아가 되거나 화성에 닿기도 전에 연료가 바닥날 수 있다. 무사히 화성에 도착하기 위해선 정확한 길을 알아야 한다. 해법은 수학을 이용한 치밀한 시뮬레이션이다. 벡터와 미적분, 타원을 바탕으로 수백만번의 가상 연습을 거쳐야, 단 한 번의 기회를 성공으로 이끌 수 있다.
화성과 가까워지는 ‘그 때’
화성으로 가는 길을 알려면 정확한 ‘때’부터 알아야 한다. 화성과 가장 가까울 때 떠나야, 가장 빨리 도착할 수 있다. 연료를 아끼고 무중력과 우주방사선에 노출되는 시간을 줄이려면 여정을 가능한 짧게 해야 한다.
지구와 화성 사이의 거리는 태양과 두 행성이 일직선에 있을수록 가깝다. 이때를 ‘충’이라 한다. 약 780일에 한 번씩 이때가 돌아온다. 그런데 ‘충’마다 거리가 다르다. 그중에서 지구가 태양에서 가장 먼 곳에 있고, 화성은 태양에 가장 가까울 때 둘 사이가 가장 가깝다. 이 순간을 ‘대접근’이라 한다.
최근 화성과 지구가 사이가 가장 좁았던 건 2003년의 일이다. 무려 5만 년만의 ‘대접근’이었다. 두 행성 사이의 거리가 5575만 8000km에 불과했다. 평균보다 2000만 km 이상 짧았다. 다행히 2105년부터 10년 동안 2003년 정도로 화성이 가까이 오는 기회가 두 번이나 더 찾아왔다. 2112년 7월과 2114년 9월이다. 지구와 화성 사이의 거리는 6000만 km 정도였다.
이런 예상은 행성의 위치를 좌표로 정확히 구할 수 있기에 가능하다. 행성의 공전 궤도는 주위 중력의 영향을 받아 조금씩 달라진다. 벡터와 미적분은 미세한 변화를 푸는 열쇠다. 중력 같은 힘은 방향과 크기를 갖는 벡터다. 벡터는 미분과 적분이 가능하다. 힘에서 구한 가속도를 시간에 따라 적분해 주면 행성의 위치를 구할 수 있다. 실제 계산은 이보다 훨씬 복잡하지만, 벡터와 미적분을 기초로 한다.
중력을 타고 화성으로~
추진력이 강한 원자력 로켓을 이용하면, 큰 고민 없이 화성으로 곧장 날아갈 수 있다. 하지만 핵전쟁이 일어나면서 지구에서 쓸 만한 원자력 로켓은 이미 모두 무기로 써버렸다. 낡은 방식이지만, 중력을 이용해야만 한다. 21세기엔 중력의 도움이 있어야 화성에 갈 수 있었다. 로켓의 힘이 화성으로 바로 가기엔 부족했기 때문이다.
화성에 가려면 지구의 중력을 벗어나 화성의 중력권으로 들어가야 한다. 강력한 에너지가 필요한 일이다. 중력을 이용한 길을 따라가면, 조금 돌아가더라도 적은 에너지로 화성까지 갈 수 있다. 바로 ‘호만 전이궤도’를 이용하면 된다.
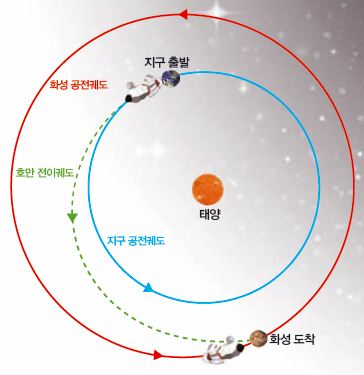
호만 전이궤도는 지구와 화성을 연결해 주는 타원 모양의 길이다. 지구 주위를 돌다 적절한 속도를 더해 주면 이 길에 접어들 수 있다. 다시 이 길을 따라 돌다가, 화성과 만나는 곳에서 다시 알맞은 속도를 더해 주면 화성 중력권으로 미끄러지듯 들어갈 수 있다.
인류는 수백만 번의 시뮬레이션을 통해, 정확한 시간과 알맞은 타원 모양의 길을 구할 수 있었다. 그리고 마침내 만반의 준비를 갖춘 선발대가 길을 떠났다.
숫자로 보는 화성
686.96일
화성의 공전주기다. 화성의 1년은 지구(365일)보다 두 배 가까이 길다. 자전주기는 24.62시간(화성)과 23.93시간(지구)으로 큰 차이가 없다. 하루는 비슷하게 흘러가겠지만, 지구 달력을 그대로 쓸 수는 없다.
-63℃
화성의 평균 기온이다. 지구의 평균 기온은 14℃다. 화성에서 지구의 옷을 입었다간 그 자리에서 온몸이 얼어버린다. 이 온도에선 농사도 지을 수 없다.
11°~49°
화성의 자전축이 변하는 범위다. 주변 중력의 영향으로 이런 현상이 생긴다. 지구는 달의 영향이 워낙 지배적이라 기울기 변화 (22°~24°)가 적다.
3.69m/s²
화성의 중력가속도다. 지구의 3분 1 정도다. 같은 힘으로 지구에서보다 훨씬 높이 뛸 수 있다. 마냥 좋아할 일은 아니다. 약한 중력은 근육과 뼈를 약하게 한다. 지구에서 보다 운동을 훨씬 더 많이 해야 한다.
95% vs 0.13%
화성의 대기 중 이산화탄소와 산소의 비율이다. 지구에선 각각 0.038%, 21%다. 산소는 절대적으로 부족하고, 이산화탄소가 대부분이다. 화성에서 살아남기 위해선, 이산화탄소를 산소로 바꾸는 기술이 필요하다.
일차함수로 1년을 버텨라
진짜 문제는 지금부터다. 화성은 사람이 살 수 없는 땅이다. 산소와 물은 없는 것이나 마찬가지고 땅은 붉은 먼지투성이다. 영하 수십 도의 온도와 강한 우주방사선도 생존을 위협한다.
선발대에겐 1년의 여유가 있다. 지구에서 1년을 버틸 수 있는 자원을 실어왔다. 1년 안에 화성을 사람이 살 수 있는 곳으로 만들어야 한다. 한정된 자원으로 1년을 무사히 버텨내려면 계획부터 철저하게 세워야 한다. 무작정 쓰다보면 자원은 금세 바닥을 보일 것이다. 마냥 아낄 수도 없는 노릇이다. 충분히 먹고 재료를 써야 지치지 않고 정해진 시간 안에 정착지를 완성할 수 있다.
답은 직선에 있다
선발대는 가져온 자원을 이용해 두 가지 영양 캡슐을 만들 수 있다. 가장 적은 재료로 필요한 캡슐을 만드는 방법은 무엇일까? 단, 캡슐은 꼭 섞어 먹어야 한다.
최적의 식단이 갖춰야 할 조건을 정리해 보자.
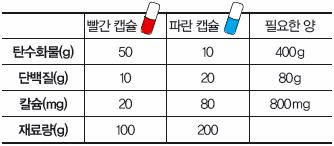
➊ 빨간 캡슐($a$개)과 파란 캡슐($b$개)을 모두 먹어야 한다.
➋ 탄수화물(50$a$+10$b$)은 400g 이상 섭취해야 한다.
➌ 단백질(10$a$+20$b$)은 80g 이상 섭취해야 한다.
➍ 칼슘(20$a$+80$b$)은 800mg 이상 섭취해야 한다.
목표: 가장 적은 재료($k$=100$a$+200$b$)로 이 조건을 모두 만족하도록 캡슐을 만들어라!
조건들은 모두 일차부등식으로 쓸 수 있다.
➊ $a, b$≥1
➋ 50$a$+10$b$≥400
➌ 10$a$+20$b$≥80
➍ 20$a$+80$b$≥800
목표: 이 범위를 만족하는 가장 작은 $k$값을 찾아라!
위 식을 이용해 그래프를 그리고 방정식을 풀면, $a=\frac{120}{19}, b=\frac{160}{19}$이 최적의 답임을 알 수 있다. 캡슐의 수는 자연수여야 하므로 빨간 캡슐과 파란 캡슐을 각각 7개, 9개씩 만드는 경우가 가장 경제적인 방법이다.
이처럼 일차함수와 방정식, 부등식을 이용해 최적의 답안을 찾는 방법을 ‘선형계획법’이라 한다. 일차식을 그리면 직선이기 때문에, 선형이라는 이름이 붙었다. 사회 곳곳에서 활약 중인 다양한 최적화 기법의 대부분이 바로 선형계획법에서 비롯됐다.
최고보다 최적을
선형계획법은 2차 세계대전 당시 효율적으로 군수 물자를 보급하고 경제적인 작전을 세우는 과정에서 탄생했다. 전쟁에 참가했던 많은 수학자들도 자연스레 선형계획법에 관심을 갖게 됐다. 미국 공군에서 통계관리 업무를 맡았던 조지 댄치그도 그 중 한명이다.
전쟁이 끝난 뒤, 댄치그는 획기적인 선형계획법을 발표한다. 바로 ‘단체법’이다. 단체법은 답일 가능성이 있는 경우부터 시작한다. 가까운 곳에 더욱 좋은 답이 있다면, 그곳으로 이동한다. 더 이상 나은 답이 보이지 않을 때, 마지막으로 머물던 곳이 최적의 답이 된다. 단체법은 정답일 가능성이 있는 경우만 찾아다니기 때문에, 풀이 시간이 크게 줄어든다.
단체법은 과정이 단순하고 응용하기가 편하다. 그래서 어떤 문제에도 적용하기 좋다. 덕분에 경영학이나 산업공학처럼 최적화가 중요한 분야에선 없어선 안 될 존재가 됐다. 수학적으로 완벽한 풀이는 아니지만, 지금 당장 필요한 답을 빨리 구할 수 있기 때문이다. 화성에서도 마찬가지다. 정해진 시간 안에 한정된 자원을 효율적으로 사용하기 위해선, 최고보다 최적이 필요하다.
남극 전문가의 조언 “화성생활, 마음먹기에 달렸다”
➊ 긍정적인 태도
스트레스는 생존율을 떨어뜨립니다. 또한 극한 환경에선 항상 돌발 상황이 생기죠. 당황하지 않고 침착하게 대응해야 큰 사고를 막을 수 있습니다.
➋ 책임감
어려운 상황일수록 ‘나 하나쯤이야’하는 생각이 공동체를 붕괴시킬 수 있습니다. 모두가 맡은 임무를 다해야, 척박한 화성에서 살아남을 수 있습니다.
➌ 존중과 배려
조그만 자극에도 반응이 커지게 됩니다. 별일 아닌 일에도 다툼이 생길 수 있죠. 어느 때보다 서로를 존중하고 배려하는 마음이 필요합니다.
Part 2 문명의 기반을 닦아라
화성 생활의 필수 요소, BIG 4!
정착할 땅을 찾은 화성인의 다음 목표는 도시 건설이다. 새로운 문명을 세우기 위해선, 도시가 필요하다. 자원과 땅이 부족한 화성에서 지구처럼 마구잡이로 도시를 지을 수는 없는 일. 합리적인 방법으로 경제적인 도시를 세우려면, 수학의 도움이 필요하다. 화성만의 도시는 어떻게 만들어야 할까? 화성 정착에 힘쓰고 있는 수학자의 이야기를 들어보자.
1 지오데식돔 보호막
화성에는 자외선과 태양풍을 막아줄 대기가 부족하고 자기장은 아예 없다. 우리는 살아남기 위해 지오데식돔 모양의 보호막을 만들기로 했다. 지오데식돔은 다면체의 면을 삼각형으로 만들어, 모양을 구에 가깝게 만든 입체 도형이다.
지오데식돔으로 만든 보호막은 튼튼하다. 어떤 방향에서 힘을 받아도, 빈틈없이 메워진 삼각형이 서로를 지탱하며 무게를 나눠 갖는다. 기둥 없이도 안정적인 구조를 유지할 수 있다.
작은 겉넓이로 가장 큰 부피를 에워싸는 구 모양이라 경제적이기도 하다. 표면적이 작아 건축 재료가 적게 필요하고 바깥으로 빠져나가는 열도 얼마 되지 않는다. 똑같은 삼각형 모양의 재료만 쓰여서, 공사 기간도 줄일 수 있다.

지구와 화성의 엇갈린 운명
지구는 자외선과 태양풍을 막아주는 대기와 자기장으로 둘러싸여 있다. 화성에는 이런 보호막이 없다. 크기가 작다보니 대기권을 붙잡아줄 중력이 약하고, 자기장을 만들어 내는 행성 내부의 운동도 오래 전에 멈췄기 때문이다. 보호막이 사라지면서, 자외선과 태양풍이 화성 표면을 깨끗이 씻어 버렸다. 그 결과, 화성 표면에는 붉은 먼지만 가득하다. 화성과 지구의 크기가 반대였다면, 운명은 달라졌을지 모른다.
2 그래프로 만든 수도 시설과 도로
화성의 수도 시설과 도로는 그래프이론을 바탕으로 만들었다. 그래프이론은 점과 점 사이를 연결하는 경로에 대해 말해준다. 수도 시설과 집은 점, 수도관과 도로는 선이라 보면 각 점을 어떻게 연결해야 할지 그래프이론으로 생각할 수 있다.
우리는 오일러 경로와 해밀턴 경로에 주목했다. 오일러 경로는 모든 선분을 한 번씩만 지나서 다시 제자리로 돌아오는 길이다. 해밀턴 경로는 모든 꼭지점을 한 번씩만 지나서 다시 출발점으로 돌아오는 길이다. 둘 다 모든 곳을 최적의 경로로 이어주기에 알맞는 모델이다. 우리는 두 가지 경로를 활용해 화성의 수도 시설과 도로 시스템을 만들고 있다. 흐르는 물체의 움직임을 알려 주는 유체 방정식도 큰 힘이 되고 있다. 자동차의 움직임도 흐르는 물과 다르지 않기 때문이다.

3 산소 만들기는 인내심 싸움
화성이 식물로 뒤덮인다면, 화성도 지구처럼 생명이 숨 쉬는 푸른 행성이 될 수 있다. 식물의 광합성이 이산화탄소를 산소로 바꿔주기 때문이다.
가장 유력한 후보는 이끼다. 화성에 가득한 이산화탄소를 먹고 자라는 이끼는 남극처럼 혹독한 환경에서도 잘 버틴다. 하지만 이끼가 화성을 뒤덮는다고 세상이 바로 달라지진 않는다. 간단한 계산을 해 보면 오랜 인내가 필요하다는 걸 알 수 있다.
화성에 필요한 산소의 질량부터 구해 보자. 화성에 필요한 대기층의 질량은 지구 대기층의 25% 정도다. 화성의 표면적이 지구의 약 4분의 1이기 때문이다. 지구의 대기가 약 5.15×10$^{18}$kg이므로, 화성에 필요한 대기는 1.29×10$^{18}$kg 정도다. 산소의 비율이 지구(21%) 같다면, 2.7×10$^{17}$kg 가량의 산소가 필요하다고 할 수 있다.
이제 화성을 뒤덮으려면 얼마나 많은 이끼가 필요한지 알아 보자. 이끼 하나가 덮을 수 있는 면적은 1cm² 남짓이다. 화성의 표면적은 1.47×10$^{8}$km²인데, 화성을 뒤덮으려면 1.47×10$^{18}$개 만큼의 이끼가 필요하다.
이끼 하나가 한 시간에 생산할 수 있는 산소량은 3.25×10$^{-10}$kg 정도다. 따라서 화성을 뒤덮은 이끼밭이 만들어 내는 산소는 시간당 4.78×10$^{8}$kg 남짓이다. 이 값으로 필요한 산소량을 나눠 주면, 5억 6500만 시간이 나온다. 지구의 시간으로 약 6만 4500년이다. 단군이 나라를 세운 다음 흐른 시간보다 훨씬 더 길다. 쑥과 마늘만 먹고 지내는 것보다 훨씬 큰 인내가 필요하다.

4 화성만의 달력
화성의 공전주기는 지구 날짜로 686.96일이다. 지구의 달력을 그대로 쓰면, 1년하고도 11개월 더 흐른 시간이다. 화성의 자전주기는 24.62시간이다. 지구의 하루보다 39분 35초 남짓 길다. 한 달은 조금 더 복잡하다. 화성에는 2개의 위성(포보스와 데이모스)이 있다. 포보스와 데이모스의 공전주기는 각각 7.66시간과 30.35시간이다. 어느 것 하나 달의 후보로 삼기 힘들다.
인류는 수천 년 전부터 1분은 60초, 1시간은 60분, 하루는 24시간, 한 달은 약 30일이라는 기준으로 살아왔다. 시계는 물론, 사회와 문화의 많은 부분이 이 습관에 따라 정해져 있다.
이 기준을 무리하게 바꿀 수는 없지만, 화성 상황에 맞게 조금 고칠 필요는 있다. 지구의 시간에 맞춰서 살다간, 달력과 계절이 상관없게 돼 버린다.
화성의 하루(24.62시간)를 24시간으로 만들어 보자. 화성의 1시간을 지구의 1시간 1분 40초로 정한다. 과거 화성탐사선들이 썼던 방식이다.
달력은 더 손질이 필요하다. 우선 새로운 1년은 668화성일(1화성일=1.027지구일)로 정했다. 12에 익숙한 우리는 24개월로 새로운 1년을 짜기로 했다. 습관을 따라, 1달은 28일 남짓으로 정했다. 6개월을 기준으로 5달은 28일, 마지막 달은 27일이 된다. 이렇게 4번 반복되면 1년이다. 약간의 오차는 2년에 한 번씩 윤년을 넣어 맞추기로 했다. 이렇게 우리는 화성의 달력을 만들었다.
Part 3 압축이 답이다
도시가 건강해야 문명이 산다
세월이 흐르면 인구는 늘고 돔은 점점 비좁아질 것이다. 문명의 성장은 한계에 부딪히고 삶의 질은 점차 나빠질 것이다. 돔만 계속 짓는다고 해결될 문제가 아니다. 선택이 필요한 순간이다. 그때부터는 도시의 몸집을 키워야 한다.
커지면 더 적게 먹고 더 많이 움직인다
도시가 커지면 여러 가지 문제가 생긴다. 마구잡이로 키운 도시는 자연 환경을 파괴한다. 숲은 사라지고 온실가스는 넘쳐난다. 대도시에선 범죄와 빈곤 같은 사회문제도 많이 일어난다. 자연스레 사람 사이와 국가 사이의 갈등이 늘어나고 전쟁까지 일어 날 수 있다.
도시의 성장이 꼭 나쁜 결과만 낳는 건 아니다. 과거 지구의 통계물리학자들은 도시의 크기와 특허출원수, 전력생산량, 임금 같은 다양한 가치들 사이의 관계를 그래프로 그렸다. 기울기가 1보다 컸다. 도시가 만들어 내는 가치가 도시의 크기보다 더 빨리 증가한다는 의미다.
도시가 2배 커지면, 한 사람당 필요한 주유소, 전력선 같은 사회기반시설은 15%씩 줄었다. 대신 임금, 특허, 저금 같은 경제적 가치는 한 사람당 약 15%가 늘었다. 1인당 전화통화량도 12% 정도 많아졌다. 한 마디로 도시는 커질수록 더 적게 먹는 대신 더 많이 움직였다. 이론대로라면, 화성에서 문명을 키우려면 도시의 몸집부터 불려야 한다.
도시도 몸무게 관리가 중요
영양이 부족하면 아이는 키가 크지 않는다. 대신 너무 뚱뚱해도 성장에 문제가 생긴다. 도시도 건강하려면 적당한 몸무게를 유지해야 한다. 예를 들어 인구가 2배가 된다고 해서 도시의 면적까지 똑같이 2배로 늘어날 필요는 없다. 1.5배만 커져도 충분하다. 수도관이나 도로 같은 시설도 마찬가지다. 양은 83%, 길이는 67%만 보충하면 문제없이 2배 늘어난 시민을 만족시킬 수 있다. 도시의 몸무게는 인구, 도로면적, 생산량 같은 수치로 알 수 있다.
몸무게를 알면 도시의 미래도 점쳐볼 수 있다. 2012년 미국 산타페 연구소의 루이스 베텐코트 교수는 임금, 특허, 통화량처럼 도시가 만들어내는 긍정적 가치(Y)와 범죄, 질병 같은 도시의 부정적 요소(W)를 뺀 수치(Y-W)와 도시의 몸무게(G) 사이의 관계를 그래프로 그렸다.
이 그래프는 도시의 몸집이 너무 커지면 도시의 활력이 떨어진다는 걸 보여 준다. 어느 이상을 넘어가면 아예 도시가 위험에 빠진다. 대신 적당한 선까지는 몸집이 커질수록, 더 많이 일한다는 사실도 확인할 수 있다. 다이어트 스트레스에는 시달리겠지만, 건강한 도시를 위해선 항상 몸무게를 신경 써야 한다.
무게로 미래의 도시를 점쳐 보자!
도시의 몸무게(G)는 도시의 총 생산량과 도로량을 곱한 값을 인구로 나누면 구할 수 있다. 시민 1명당 얼마나 생산하고 이동할 수 있는지 나타내 준다.
G = $\frac{도시의 총 생산량(원)×도시의 도로량}{도시의 인구(명)}$
더 많이 일하고 도로를 늘리면 몸집이 커지면서, 도시가 성장한다. 하지만 몸무게가 어느 이상 늘어나면, 도시는 병들고 몰락하기 시작한다.

우리나라에서 가장 무거운 도시는?
우리나라에서 몸무게가 가장 무거운 도시는 울산이다. 공장이 많아 도로가 넓고, 평균 임금도 높다. 가장 가벼운 도시는 인천이다. 인구에 비해 도로가 부족하다고 볼 수 있다.
최대한 줄이고 좁혀라
화성의 압축도시
지구에서 흔히 볼 수 있던 도시 형태는 분산 도시다. 분산 도시는 넓은 지역이 도시의 기능을 나눠 갖는다. 서울과 주변의 위성도시를 떠올리면 이해가 쉽다. 도시가 발전하면 중심지역의 땅값은 점점 비싸진다. 공장과 주택은 자연스레 도시 외곽으로 옮겨간다. 도시의 범위가 점점 넓어지면서, 사람들의 이동거리는 점점 길어진다. 자연스레 도로가 많아지고 녹지는 줄어든다. 자동차 이용이 늘어나면서 에너지를 많이 쓰게 되고, 공기도 나빠진다. 도시가 넓어질수록, 산과 숲 같은 녹지가 줄어든다는 점도 문제다.
화성의 도시는 반드시 보호막(돔) 안에 있어야만 한다. 따라서 화성의 도시는 압축도시가 될 수밖에 없다. 압축도시는 주거·상업·행정 같은 도시의 기능을 좁은 지역에 빽빽하게 몰아넣은 도시다. 압축도시라는 이름은 두 명의 수학자가 붙여 줬다. 그중 한 명이 단체법을 만들어 낸 조지 댄치그다. 지금은 화성에 압축도시를 짓기 위해 노력하는 수준이지만, 더 먼 미래에 우리의 후손은 우주 곳곳에 이런 도시를 짓고 살아갈지도 모른다.
푸른 나무의 도시
멀리서 본 화성의 도시는 마치 거대한 나무 같다. 모든 건물은 벽면이 이끼로 덮여 있기 때문이다. 돔 안의 공기를 깨끗하게 유지하기 위한 노력의 결과다. 작은 중력을 활용해, 빌딩 위아래로 움직이는 셔틀버스도 설치했다.
모든 길은 지하로 통한다
압축도시에서 철도, 고속버스같이 먼 곳으로 가는 교통수단은 모두 지하로 다닌다. 부족한 화성의 녹지를 지키기 위해서다. 지하에 있는 대신, 경로가 단순해지다 보니 교통 체증은 훨씬 줄어든다. 그만큼 에너지도 아낄 수 있다.
좁지만 효율적
압축도시의 기능은 한 곳에 집중돼 있다. 자고 일하고 쇼핑하는 일이 좁은 장소에서 반복된다. 이동거리가 짧으니, 온실가스가 적게 생기고 교통비도 적게 든다. 에너지의 사용과 배출이 모두 한 곳에서 이뤄지다 보니, 에너지 효율과 재활용 비율도 모두 높다.
화성의 푸른 땅
압축도시의 땅 위에는 자동차가 없다. 덕분에 땅 대부분을 녹지로 보호할 수 있다. 녹지는 보기에 좋을 뿐만 아니라, 대기오염물질을 없애는 데도 도움이 된다. 사방이 온통 푸르다 보니, 가끔은 화성에 있다는 사실마저 잊어버린다.











