아침을 먹으면 수학 실력이 오른다?!
미국 아칸사스대 소아과 테리 피빅 교수는 아침을 먹으면 수학 점수가 높아진다는 흥미로운 연구 결과를, 지난해 1월 미국 농무부 학술지에 발표했어요.
연구팀은 아침식사와 수학 점수 사이의 관계를 밝히기 위해, 8세에서 11세의 초등학생 81명을 두 그룹으로 나누어 실험을 진행했어요. 40분 간격을 두고 학생들에게 2번의 수학 시험을 치르게 했죠. 두 그룹은 모두 8시간씩 잠을 잤고, 한 그룹에게만 첫 번째 수학 시험 후 아침을 먹게 했어요. 그리고 학생들이 문제를 푸는 과정에서 발생하는 뇌파를 관찰했어요.
그 결과 중간에 아침을 먹은 학생들의 수학 점수가 더 높은 것을 확인할 수 있었어요. 뿐만 아니라 아침을 먹은 학생들은 먹지 않은 학생들에 비해 더 적은 뇌 활동으로 더 빨리 문제를 푸는 것도 알 수 있었답니다.

⇒ 수학동아 클리닉 코멘트
아침 식사는 뇌 활동을 활성화합니다. 그러면 식사를 하기 전보다 생각하는 힘이 더 생기죠. 따라서 아침식사 후 수학 문제를 풀면 이전보다 더 좋은 점수가 나올 확률이 높습니다. 하지만 점수가 50점이었던 친구가 아침을 먹는다고 해서 갑자기 100점을 맞는 기적은 일어나지 않죠. 그래도 분명한 건 집중력 향상에 도움이 된다는 사실입니다!

수학 공포증, 원인은 유전자 탓?!
미국 오하이오 주립대 스테픈 페트릴 교수팀이 수학에 대한 불안감의 일부는 부모에게 물려받은 유전자 때문이라는 연구 결과를 발표했어요. 이 결과는 지난해 5월 ‘소아심리정신과학저널’에 실렸답니다.
연구팀은 오하이오에 사는 일란성 쌍둥이 216쌍과 이란성 쌍둥이 298쌍을 대상으로 연구를 진행했어요. 수학에 대한 불안감, 일반적인 불안감, 독해력, 수학 문제 해결력의 4가지 요소를 초등학교 저학년 때 처음 측정한 다음, 9~15살이 될 때까지 최대 8번에 걸쳐 꾸준히 관찰하면서 어떻게 변화하는지를 지켜봤어요.
그 결과 수학에 대한 불안감을 형성하는 원인의 40%는 유전적인 요인에 따르는 것으로 밝혀졌습니다.
페트릴 교수는 “수학에 대한 불안감이 모두 유전자 탓이라고는 할 수 없다”고 말하면서도, “유전으로 전해진 수학 공포증을 가지고 있는 학생이 만약 수업 시간에 수학에 대한 부정적인 경험을 한다면, 그렇지 않은 학생에 비해 반응속도가 더 빠를 것”이라고 말했어요.
⇒ 수학동아 클리닉 코멘트
페트릴 교수의 말처럼 수학 공포증이 100% 유전되지는 않을 겁니다. 하지만 부모님이 자녀에게 ‘불안한 마음’을 들키면, 자녀는 덩달아 불안한 마음이 생길 수밖에 없죠. 그렇기 때문에 수학 공포증을 이겨내기 위해서는 끊임 없이 ‘나는 할 수 있다’라고 자기 암시를 해야 하며, 아주 작은 목표부터 이루면서 ‘성취감’을 경험하는 게 중요합니다. 그래야 자신감이 생길 테니까요!
손짓을 많이 하면, 수학 문제 일반화에 도움 된다?!
미국 시카고대 심리학과 미리암 노박 박사팀은 손짓을 사용하면 수학 문제를 이해하는 데 도움이 된다는 연구 결과를 지난해 4월 ‘미국 심리과학학회 학술지’에 발표했어요.
연구팀은 초등학교 3학년 학생 90명을 대상으로 ‘등식의 동치 문제’를 풀어 보게 했어요. 등식의 동치 문제란 등호(=)를 기준으로 양변의 값이 같도록 만드는 문제를 말해요.
연구팀은 학생들을 세 그룹으로 나눠 서로 다른 방법으로 한 문제를 풀게 했어요. 2+9+4=□+4에서 □에 들어갈 알맞은 수를 찾는 문제였답니다.
첫 번째 그룹은 숫자 자석을 자유롭게 이용했고, 두 번째 그룹은 자석은 사용하되 손으로 움직이는 시늉만 했어요. 마지막 그룹은 손짓을 이용해 □에 들어갈 수를 찾도록 했어요. 여기서 손짓이란 왼쪽 사진처럼 손가락을 v자로 만들어 빈 칸에 들어갈 수를 더 빠르게 유추할 수 있는 방법을 말해요.
실험 결과, 손짓을 사용한 세 번째 그룹의 정답률이 가장 높았어요. 노박 박사님은 “손짓은 수업 중에 배운 지식을 일반화시키는 가장 효율적인 방법”이라고 설명했어요.

⇒ 수학동아 클리닉 코멘트
손짓은 수학 문제를 시각화하는 데 큰 도움이 됩니다. 예를 들어 어린 아이들이 2+3과 같은 간단한 연산을 할 때 손가락의 도움을 받는 것과 같은 원리죠. 하지만 이 연구 결과는 ‘등식의 동치 문제’라는 한 유형만 분석한 결과입니다. 만약 지금 이 글을 읽고 있는 당신이 초등학교 고학년 이상이라면, 고개를 갸웃거릴지도 모릅니다. 이미 손가락셈은 졸업을 했을 테니까요. 하지만 눈에 보이지 않는 수학 문제를 빠르게 시각화해 정답을 생각하는 과정에서 ‘손짓’은 도움이 됩니다.



여기서 수학 체질이란 ‘수학을 대하는 나의 습관과 태도’를 말한다. 사람마다 평소 수학을 공부하는 습관이나 수학을 생각하는 마음가짐이 다르기 때문에 수학 체질을 알면 자신의 문제점을 알기 쉽다.
일본의 유명한 수학 저술가 나가노 히로유키는 수포자가 학년이 올라갈수록 증가하는 이유를 설명했다.
“수포자 중 절반 이상이 저학년 때 ‘산수’를 좋아했던 학생입니다. 산수를 공부할 때는 이미 잘 짜여진 계산 알고 리듬만 익히면 수를 대입해 충분히 고득점을 얻을 수 있었는데, 학년이 올라갈수록 접하는 수학 문제는 이 방법만으로 고득점을 받을 수 없기 때문이죠.”
그래서 수학자들은 꽤 오래 전부터 ‘문제 해결 방법’에 집중했다. 단순한 연산 문제를 제외하고는 수학 문제라면 식과 풀이과정이 반드시 필요하기 때문이다.
문제 해결 방법은 크게 두 가지로 나눌 수 있다. 하나는 ‘수학 알고리듬’을 이용하는 방식이고, 또 다른 하나는 ‘발견술’을 기초로 생각의 물꼬를 터 가는 방식이다.
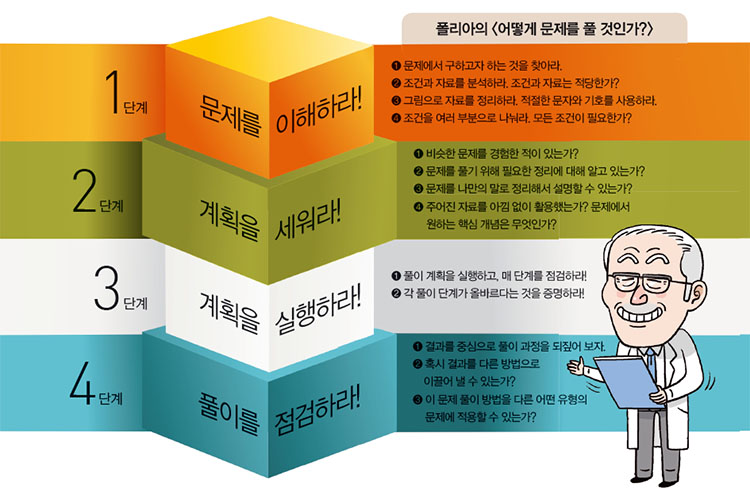
예를 들어 ‘그래프를 보고 함수식을 구하라’는 문제는 다음과 같은 알고리듬에 따라 정답을 구한다.

이 방식은 정답을 찾을 확률이 꽤 높다는 장점이 있지만, 알고리듬 방식은 적용할 수 있는 문제의 범위가 매우 좁다는 단점이 있다.
문제 해결 방식에 발견술을 적용해 보자!
지금까지 수학 알고리듬에 수만 바꿔 대입해 기계적으로 문제만 풀었던 학생이라면 다음 이야기에 집중해 보자. 발견술이라 불리는 문제 해결 방법은 기존의 알고리듬 방식과 달리 좀 더 여유있게 문제에 접근한다.
먼저, 발견술이 무엇일까? 이름부터 생소하다. 사실 발견술이란 생소하거나 어려운 문제 상황에 직면했을 때, 그것을 어떻게 해결할지 생각하는 전략, 때론 논리에 대한 이야기다. 발견술의 목표는 발견하는 방법과 규칙을 논리에 따라 정리하고 연구하는 것이다. 발견술은 알고리듬 방식과 달리 연산, 대수, 기하, 측정 네 영역 어디에도 적용할 수 있다.

문제 해결 방식에 발견술을 적용해 보자!
지금까지 수학 알고리듬에 수만 바꿔 대입해 기계적으로 문제만 풀었던 학생이라면 다음 이야기에 집중해 보자. 발견술이라 불리는 문제 해결 방법은 기존의 알고리듬 방식과 달리 좀 더 여유있게 문제에 접근한다.
먼저, 발견술이 무엇일까? 이름부터 생소하다. 사실 발견술이란 생소하거나 어려운 문제 상황에 직면했을 때, 그것을 어떻게 해결할지 생각하는 전략, 때론 논리에 대한 이야기다. 발견술의 목표는 발견하는 방법과 규칙을 논리에 따라 정리하고 연구하는 것이다. 발견술은 알고리듬 방식과 달리 연산, 대수, 기하, 측정 네 영역 어디에도 적용할 수 있다.

고대 수학자들 중에는 유클리드가 가장 먼저 이 발견술에 대해 언급했다. 그 뒤로는 파푸스, 데카르트, 라이프니츠 등이 관심을 보였고, 체코의 수학자 베르나르트 볼차노가 18세기에 들어 자신의 저서에서 발견술에 대해 꽤 비중 있게 이야기했다.
현대에 들어 가장 먼저 문제 해결 방법에 발견술을 적용한 수학자는 1954년 헝가리의 수학자 조지 폴리아다.



수학을 잘 하려면 가장 중요한 기본기가 무엇이냐는 질문에 이영하 이화여대 수학교육과 교수는 망설임 없이 ‘구구단’과 ‘분수의 사칙연산’이라고 대답했다. 또한 김래영 이화여대 수학교육과 교수는 “학생들에게 수학이 어렵게 느껴졌던 첫 순간을 물으면, 대부분 ‘나누어 떨어지지 않는’ 나눗셈 연산을 만났을 때”라는 대답이 가장 많다고 말했다.
초등학교 저학년 때부터 줄곧 만점을 받던 학생들도, 나머지를 생각해야 하는 34÷6과 같은 나눗셈은 반가울 리 없다.이렇게 나누어 떨어지지 않는 자연수의 나눗셈은 학년이 올라가면서 ‘분수’라는 개념이 더해져 확장된다. 그러면서 4학년 이후 분수의 덧셈부터 시작해 차근차근 분수의 사칙연산을 배운다. 분수의 연산을 자유롭게 하려면 대분수를 가분수로 만드는 것부터 시작해서 통분, 약분, 기약분수 등 익혀야 할 개념과 문제 풀이 알고리듬이 꽤 많다. 그런데 이때 개념을 제대로 익히지 않고 계속 다음 학년으로 올라간다면, 앞으로 만나게 될 인수분해며 고차방정식이며 다항함수며 모두 분수 때문에 어려움을 겪을 수도 있다. 분수를 잘 안다고 자만하지 말고, 이번 기회에 기본 개념을 확실히 알고 가자!



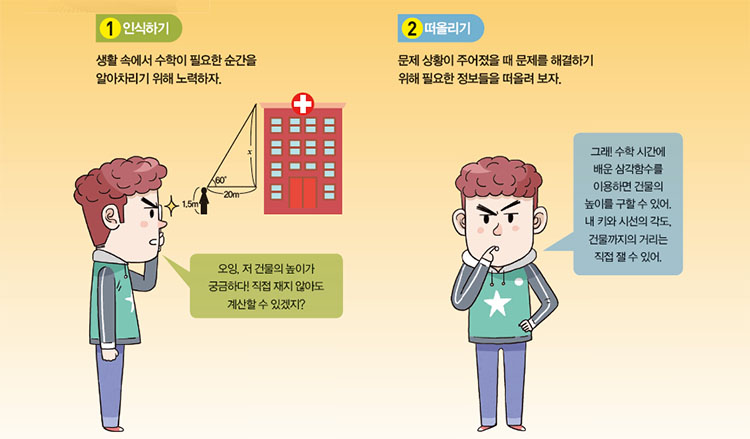
폴리아 교수가 발견술을 중심으로 문제 해결 방법을 발표했을 때, 당시 수학교육자들은 체계적으로 잘 정리된 질문과 내용에 박수를 보냈다. 하지만 그로부터 꽤 오랜 시간이 흘렀기 때문에, 폴리아의 방법은 교육 정책과 시대의 흐름에 영향을 받으며 계속해서 후배 수학 교육자들에 의해 발전을 거듭해 왔다.
특히 세계적으로 권위 있는 수학교육자인 미국 캘리포니아대 버클리캠퍼스 수학교육과 앨런 숀펠드 교수는 앞서 설명했던 발견술과 더불어 인지과학 이론을 활용해 생각하는 습관이 수학교육에 미치는 영향에 대해 여러 편의 논문을 발표했다.
숀펠드 교수는 특히 ‘메타인지’ 학습법에 집중했다. 메타인지란 내가 무엇을 알고 모르는지를 파악하고, 그 부분을 보완하기 위해 계획을 세우고, 계획을 실행하고, 이를 다시 평가하는 과정을 모두 아우르는 용어다. 이 능력이 뛰어난 사람은 어떤 일을 수행하거나 배우는 과정에서 필요한 자신의 행동을 빠르게 선택할 수 있고 좋은 결과를 얻기 위한 전략을 세우기도 수월하다. 그렇다면 메타인지 능력을 키우려면 어떤 훈련을 해야 할까?
예를 들어 수학 시간에 ‘도형의 합동’에 대해 배우고 있다. 이때 두 도형이 서로 합동이려면 대응하는 변의 길이와 각의 크기가 서로 같아야 한다는 두 성질을 잘 알고 있다. 그런데 구체적으로 삼각형의 합동조건은 설명하기가 어렵다. 그래서 ‘아! 수업시간이 끝나고 삼각형의 합동조건에 대해 다시 한 번 정리해야지’라고 떠올리면 메타인지 학습법을 위한 첫 단추를 잘 꿴 것이다.
그럼 이제 한 단계 더 나아가 보자. 삼각형의 합동조건을 정리해 보니 3가지다. 이것을 한번에 공부할지 말지 ‘계획과 전략’을 세우는 것도 메타인지 학습법의 일부다.
평소에 주위에서 수학 문제를 발견하고 풀이를 생각하는 연습을 하는 것도 도움이 된다. 아직 메타인지 학습법에 대한 감이 오지 않는다면, 다음 5단계를 따라 실천해 보자.
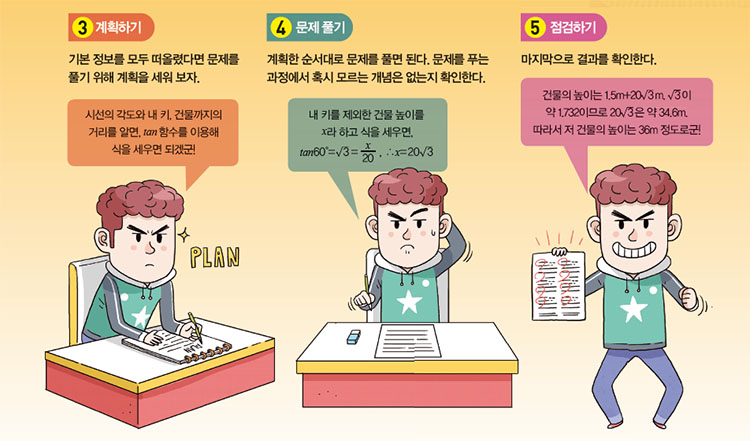

수학을 더 잘하고 싶다면, 선행학습에 목숨 걸기보다 현재 나의 상태를 먼저 파악해야 한다. 이쯤해서 수학이 싫다면 왜 싫은지, 수학 문제가 풀기 싫어서인지, 같은 실수를 반복하는 내가 싫은 건지, 노력해도 점수가 잘 오르지 않아서 좌절하는 건지 나 스스로 돌아볼 필요가 있다. 그런 다음 앞에서 소개한 전문가들의 조언대로 순서에 따라 논리적으로 생각하는 연습을 해 보자.
숀펠드 교수는 문제 상황과 맞딱뜨렸을 때, 그 결과뿐만 아니라 결과를 이끌어내기까지 생각하는 과정 자체가 매우 중요하다고 강조했다. 그래서 그는 폴리아의 발견술과 자신이 연구한 인지과학 이론을 더해 다음과 같은 4가지 중요 요소를 정리하고, 생활에 반영하라고 제안했다. 수동이의 등굣길을 관찰하며 마지막으로 발전된 방법은 어떤 내용인지 함께 알아 보자.
✚ 수동이의 등굣길, ‘수학으로 생각하기’
시작하기 전에 : 이런 훈련은 억지로 공부하기보다는 스스로 주변 환경을 관찰하며 우연히 떠오른 수학적 아이디어로 시작해 생각을 구체적으로 발전시키는 방법입니다.
❶ 자원
문제를 해결하기 위해 개인이 사용할 수 있는 도구와 기법-문제와 관련된 수학적 지식, 직관, 문제 풀이 알고리듬 등.
● 수동이의 자원 : 학교에서 수학 시간에 최대공약수, 최소공배수에 관한 내용을 배움, 주어진 수들의 공약수와 공배수를 구할 수 있고, 그 성질을 정확하게 이해하고 있음.
❷ 발견술
생소하고 낯선 문제를 만났을 때, 이것을 해결하기 위한 전략과 기술-유추하기, 일반화하기, 특수화하기, 보조문제 이용하기, 거꾸로 풀기 등.
● 수동이의 상황 : 학교까지 가는 노선이 서로 다른 세 종류의 버스가 있다. 1번 버스는 5분에 한 대씩, 2번 버스는 7분에 한 대씩, 3번 버스는 10분에 한 대씩 다닌다고 한다. 이 세 버스가 방금 한꺼번에 도착했다. 세 버스는 몇 분에 한번씩 같은 정류장에서 만날까?
● 수동이의 발견술 : 수동이는 세 버스가 만나는 시간에 대한 궁금증이 생겨 스스로 공배수의 개념을 떠올린다. 이 문제를 해결하기 위해 5의 배수, 7의 배수, 10의 배수를 나열해 보거나, 알고 있던 최소공배수를 구하는 알고리듬으로 더 빠르고 간결하게 구할 수도 있다.
❸ 통제
자원의 전략적 선택과 이를 수행하기 위한 전반적인 결정 능력-계획하기, 평가하기, 의사결정, 메타인지 학습법으로 생각하기.
● 수동이의 통제 : 발견술 과정을 통해 얻게 된 정보로 문제 풀이 계획을 세우고 실행한다. 학교에 가는 시간 동안 버스에 앉아 궁리해 보기도 하고, 학교에 도착하면 자투리 시간에 수학교과서를 꺼내 개념을 다시 한 번 떠올려 보기도 한다.
❹ 신념
학습자가 수학에 대해 가지고 있는 가치관이나 선입견.
● 수동이의 신념 : 어쩐지 수학이 우리 생활 가까이에 있는 것 같은 느낌이다.

각자의 수학 잠재 능력은 40분 동안 문제를 얼마나 잘 푸느냐로 판단할 수 없다. 그렇다면 수학 능력은 어떻게 평가할 수 있을까? 중요하긴 한 걸까?
전문가들은 입을 모아 곧 ‘수학의 시대’가 온다고 말한다. 수학을 기초로 만들어진 컴퓨터가 이미 삶의 많은 영역에 들어와 많은 역할을 대신하고 있기 때문이다.
이영하 이화여대 수학교육과 교수(이대부속고등학교 교장)는 기자에게 수학을 잘 하고 싶은 학생들에게 해주고 싶은 이야기가 있다며 전해 달라고 했다.
“컴퓨터 덕분에 편리해진 세상은 정말 살기 좋은데, 사람들이 몸이 편해지니까 생각이 게을러져요. 생각은 나만 아는 특별한 것이기 때문에 다른 어떤 누구에도 들키지 않고 게을러지기 쉽죠. 근데 생각이 게을러지면, 수학 능력도 게을러져요. 수학만큼 부지런하게 공부해야 하는 과목도 없거든요. 만약 수학을 더 잘하고 싶다면, 끊임없이 ‘왜?’라고 생각하고 게을러지려고 하는 마음을 다그치세요. 자신이 가지고 있는 잠재 수학 능력을 깨울 수 있는 사람은 오직 자기 자신뿐이라는 걸 잊지 마세요!”