d라이브러리

자연계에는 자연스러운 연산구조를 가진 사물들이 의외로 많다고 이미 강조한 바 있다. 이번호에서는 7월호에서 언급했던 공간 기하 그 자체의 연산을 발견한 헤르만 그라스만의 업적을 되새겨 보자.

연산과 기하

과학의 역사를 거슬러 올라가다 보면 추상적인 개념을 구체화하는 직관이 놀랍도록 많이 변하는 과정을 볼 수 있다. 가령 어떤 역사학자들에 의하면 고대 그리스에서는 임의의 수 4개의 곱은 의미 없는 양으로 여겨졌다고 한다. 실수 체계의 개념이 대수적으로 정립되기 전에 수는 ‘길이’의 의미로 파악됐기 때문이다. 즉, 수 하나가 길이라면 수 2개의 곱은 면적이고, 수 3개의 곱은 부피로 볼 수 있다. 하지만 4개 이상의 곱은 기하학적인 해석이 불가능하다.

물론 지금도 정수나 유리수의 세계를 넘어서 실수에 대한 직관을 키우려면 실수를 직선상의 점과 동일하게 여기는 것이 보통이다. 그리고 이런 시각적인 연습은 초등학교 수준에서 교육적으로 유용하게 사용된다.

수를 길이로 해석하고자 할 때, 나는 학생들에게 가끔 다음과 같은 질문을 한다. 직선상에 점 A와 B가 놓여 있으면 A+B를 정의할 방법이 있는가 하는 것이다(그림❶).
 
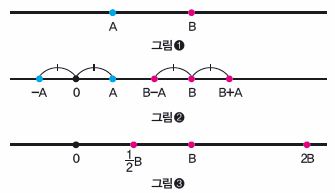
조금 생각한 후에 나오는 답은 ‘원점’이 필요하다는 것이다. 즉, 점을 하나 골라서 0이라고 이름을 붙이면 그때부터는 임의의 두 점을 더하고 뺄 수 있다. 또한 점 A가 주어지면 -A란 점도 자연스럽게 결정된다(그림❷).

여기서 한 가지 주목할 만한 사실은 점들을 굳이 수로 해석할 필요가 없고, 자연스러운 거리 관계만을 가지고 점끼리 연산한다는 것이다. 즉, 이 단계에서 거리의 단위는 전혀 필요 없다고 볼 수도 있다. 또 하나 재미있는 것은 점 A와 -A 중 어느 쪽이 양수인지 정할 필요도 없다는 것이다. 우리는 보통 직선을 수평으로 그린 후 0점의 오른쪽을 양수로 생각하는 습관이 있지만, 그것도 종이를 돌려서 보면 임의적이라는 것을 알 수 있다.

이처럼 연습한 후에는 곱셈 AB를 어떻게 하는지도 생각해 보라. 그러면 0점만 가지고는 부족하다는 것을 금방 알게 된다. 그런데 2B, 1/2B 등 실제 수와 B 사이의 곱은 정의할 수 있다(그림❸).

그렇지만 0점만 가지고는 A를 수로 생각할 수 없는 것이 문제다. 그러니까 곱셈을 정의할 때는 0만 가지고는 부족하고, 1을 정해야 한다. 그러면 단위를 하나 정하는 것과 같기 때문에 A도 수와 대응이 되어 AB에 대응되는 점을 찾을 수 있다. 다시 정리하자면, 직선상의 점의 길이를 대응시키기 위해서는 0이 필요하고, 수를 대응시키기 위해서는 0과 1이 둘 다 필요하다.

기하의 연산

그런데 때로는 단위를 정하기 전에 AB를 정의하기 위해서 ‘면적’의 개념을 사용할 수도 있다. 그러니까 AB를 직선상의 점으로 생각하지 말고, A와 B를 변으로 갖는 직사각형의 면적으로 정의할 수도 있다(그림❹). 면적도 결국 수가 아니냐고 항의할 수도 있지만, 사실 면적은 그 자체로 정의가 잘 된 개념이고 수로 해석하는 데는 또 다른 단위가 필요하다. 이 말의 뜻을 이해하려면, 면적 두 개의 크기를 비교해 보라(그림❺). 어느 쪽이 큰지를 정하는 데 사실은 단위가 전혀 필요하지 않다.
 
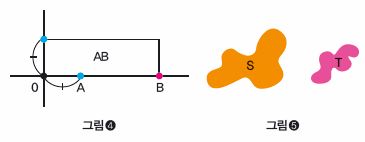
그런데 여기서 또 한 가지 가능한 반박은 면적 AB를 정하려고 A와 B에 대응되는 변들의 방향을 임의로 정하지 않았느냐는 것이다. 그러니까 곱을 구하기 위해서 평면 기하를 이용하기 시작했지만, 그러면 가능한 여러 방향이 생겨버린다. 이 때문에 사실은 길이 A보다 ‘방향이 주어진 길이’를 생각하는 것이 자연스럽다.

‘방향을 가진 거리’라면 바로 화살표로 표기하는 ‘벡터’다. 따라서 우리는 단위 없는 길이 그 자체의 곱을 찾는 과정에서 자연스럽게 벡터와 벡터의 곱을 생각하게 됐다.

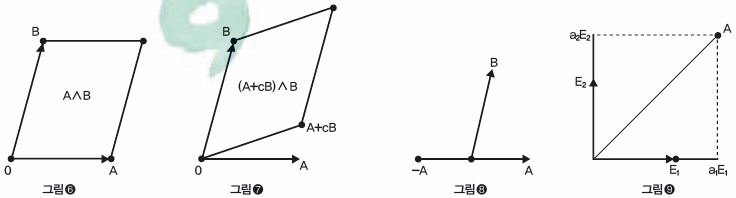
벡터 A와 벡터 B의 곱을 ‘A∧B’로 표기하기로 하자. 이 곱의 합당한 해석은 근본적으로 A와 B를 변으로 갖는 평행사변형의 면적이다(그림❻). 평행사변형의 면적을 따로 생각하기 힘들면 A∧B를 평행사변형 그 자체로 생각하는 것도 괜찮다. 그런데 자연스러운 연산의 법칙들이 여전히 적용된다고 간주하면 작은 기하학적 기적이 일어난다. 연산법칙 중 하나는 A와 B가 같은 방향이거나 반대 방향이면 A∧B=0이라는 것이다. 면적이 0인 평행사변형이 생기게 된다.

또한 대수적인 분배법칙이 성립한다고 가정하자. (A+B)∧C=A∧C+B∧C이다. 물론 이렇게 되려면 오른쪽의 합이 의미하는 바를 알아야 한다. 그런데 평행사변형 두 개의 합집합도 면적을 갖기 때문에 궁극적으로는 합집합의 면적처럼 해석하려고 한다. 그러면 분배법칙에 의해서 임의의 상수 c에 대해 (A+cB)∧B=A∧B+(cB)∧B가 성립해야 한다. 여기서는 (cB)∧B=0이므로 (A+cB)∧B=A∧B가 된다. 그런데 이것은 면적이 같은 평행사변형을 동일하게 여기는 것과 거의 같은 이야기다(그림❼).

다만 한 가지 주의할 점은 분배법칙과 0∧B=0이 된다는 법칙을 적용하면, (-A)∧B=-A∧B가 되어야만 한다는 것이다. 그런데 평행사변형의 -는 무엇일까? 그림❽을 보면 (-A)∧B는 변에서 B와 A의 역할을 바꿨을 때와 같다.(종이에 그려서 뒤집는다고 생각해 보라.) 그러니까 -A∧B=B∧A여야 한다.

따라서 우리가 평행사변형으로부터 보존하는 정보는 면적과 일종의 ‘방향성’이다. 그런데 일직선상에 놓이지 않은 벡터 E₁과 E₂를 고정시키면, 임의의 평면벡터 A를 A=a₁E₁+a₂E₂ 꼴로 표현할 수 있다(그림❾). 마찬가지로 B=b₁E₁+b₂E₂로 쓰면 A∧B=(a₁b₂-a₂b₁)E₁∧E₂임을 확인할 수 있다. 그러니까 모든 평행사변형은 E₁∧E₂ 하나의 상수 곱으로 표시되고, 벡터들의 곱은 평행사변형의 ‘방향성 있는 면적’으로 해석된다.

그라스만 대수

3차원 그라스만 대수를 엄밀히 정의하자면 실수 8개의 순서쌍 R⁸개에 주어진 수 체계의 구조다. 덧셈은 (a₀, a₁, …, a₇)+(b₀, b₁, …, b₇)=(a₀+b₀, a₁+b₂…, a₇+b₇)로 정의하지만, 곱셈의 구조는 다음과 같이 복잡하다.



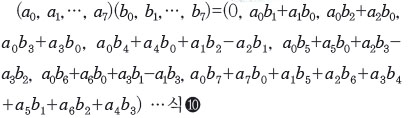
그런데 이 복잡해 보이는 곱셈은 벡터와 평행사변형의 연산을 한 차원 올려서 평행다면체 연산으로 확장하면서 자연스럽게 설명된다. 그러니까 이제는 벡터 3개의 곱 A∧B∧C나, 평행사변형과 벡터의 곱을 평행다면체의 부피와 방향성으로 해석하자는 것이다.

그런데 또 평면상에 놓여 있지 않은 벡터 3개 E₁, E₂, E₃를 고정시키면 임의의 벡터 A는 A=a₁E₁+a₂E₂+a₃E₃로 표현될 수 있고, 임의의 평행사변형은 $E₁∧E₂, E₂∧E₃, E₃∧E₁ 3개의 적당한 상수배합으로 표현할 수 있다. 그런가 하면 3차원 공간 속에서의 평행다면체는 E₁∧E₂∧E₃의 상수배로 표현된다. 실수 8개의 쌍을 점, 벡터, 평행사변형, 평행다면체의 상수배합인 a₀+a₁E₁+a₂E₂+a₃E₃+a₄E₁∧E₂+a₅E₂∧E₃+a₆E₃∧E₁+a₇E₁∧E₂∧E₃로 생각하면 곱셈을 기억하기 쉽다. 그러면 상수 a₀은 모든 벡터, 사변형, 다면체 등에 상수배로 작용하고, 위에서 거론한 벡터의 곱, 그리고 A∧B=-B∧A, 또 분배법칙에 의해서 곱셈(식❿)이 결정된다.

여기서 설명한 기하대수 구조는 19세기 중반에 헤르만 그라스만에 의해서 임의의 다차원 공간으로 확장됐다. W.K 클리퍼드는 이 연구에 기초해서 기하 대수의 일종의 ‘제곱근’을 내포하는 클리퍼드 대수이론을 개발했다. 이런 종류의 신기한 기하학은 폴 디락에 의해 페르미언 입자들의 구조적 연구에 적용되어, 결국은 20세기 후반부터 ‘초대칭성’ 이론의 기반으로 진화했다.

요즘 들어서 피타고라스가 말한 ‘모든 것이 수다’라는 격언에 대해 생각할 기회가 많은 가운데, 이번 달에는 기하 자체를 연산할 수 있는 방법을 정립한 그라스만의 대수학을 복습하고자 했다.