
“조금만 더 올라가면 된단다. 근데 말이야, 끝이 없는 계단도 있을까? 계단을 올라가고 또 올라가도 끊임없이 나타나는 계단 말이야.”
“에이, 세상에 그런 계단이 어디에 있어요? 공포영화에나 나오는 계단이라면 모를까….”
“아빠가 언제 허튼소리 하는 거 봤니? 있으니까 물어본 거지. 이참에 끝없는 계단을 만들어 보자꾸나.”
2차원에서만 가능한 무한 계단
계단을 오르는 사람이 있다. 이 사람은 단 한 번도 계단을 내려온 적 없이 계속해서 계단을 오르고 있다. 그런데 어느 순간 이 사람을 바라보니, 첫 번째 계단을 오르고 있다. 어떻게 지나온 계단으로 다시 돌아온 걸까?
그 이유는 펜로즈 계단을 오르고 있기 때문이다. 펜로즈 계단은 끊임없이 올라가거나 내려가도 항상 제자리로 돌아오는 구조를 가지고 있다. 우리 눈의 착각을 이용해 현실에서는 존재할 수 없는 계단을 2차원 그림으로 나타낸 것이다.
현실에선 불가능하지만 종이 위에선 가능한 매력적인 이 계단은 예술가의 마음을 단번에 사로잡았다. 마우리츠 코르넬리스 에스허르(에셔)도 그 중 한 사람이다. 그는 <;상승과 하강>;이라는 작품을 통해서 펜로즈 계단을 선보였다.
에스허르는 수학자의 연구를 바탕으로 작품을 제작할 정도로 수학에 대한 관심이 남달랐다. 이 때문에 에스허르의 작품은 수학자들에게 관심의 대상이었다. 실제로 일본의 수학자 스기하라 고키치는 에스허르의 작품을 보고 큰 감명을 받아, 불가능한 도형을 입체화하는 작업에 몰두하기도 했다.
대개 그림으로만 가능한 도형을 3차원으로 형상화하면 잘려나간 부분이 생긴다. 현실에서는 잘린 부분이지만 보는 각도에 따라서 이어진 것처럼 보여, 2차원에서는 끊어진 부분 없이 표현할 수 있다.
그런데 스기하라 교수는 3차원에서도 잘려 나간 부분을 만들지 않고, 이어진 형태로도 불가능한 도형을 만들 수 있다고 주장했다. 그리고 기하학적 원리와 눈의 착각을 이용해 잘려 나간 부분이 없는 불가능한 도형을 실제로 만들어 냈다.


아하! 실험 플러스 펜로즈 계단의 비밀
펜로즈 계단을 3차원에서 구현하면 사각형의 한 부분이 끊어진 계단이 된다. 즉 가장 낮은 계단과 높은 계단 사이가 뚝 끊어져 있다. 하지만 보는 각도에 따라 하나로 이어져 보인다. 왜 이런 현상이 일어나는 걸까?

뚝 끊어져 있는 계단이 하나로 연결된 계단처럼 보이는 방향을 $z$축, 가장 낮은 계단과 $z$축이 만나는 점을 원점 O라고 하자. 그러면 가장 높은 계단과 $z$축이 만나는 점 P는 (0, 0, $z$)가 된다. 그런데 $z$축과 같은 방향에서 점 P를 바라보면 $z$축이 압축돼 사라지면서 원점 O와 점 P 모두 (0, 0)이 된다. 즉 한 점이 된다.
3차원 입체는 높이와 폭, 그리고 깊이를 가지고 있다. 그런데 보는 위치에 따라서 깊이 정보가 일시적으로 소실되기도 한다. 즉 $z$축이 소실되는 위치에 끊어진 부분이 위치하면 마치 연결된 것처럼 보이는 것이다.
2차원에서는 구현 가능한 불가능한 도형을 3차원에는 나타낼 수 없는 것도 이같은 이유다. 입체를 평면에 그리면 입체가 가진 깊이 정보는 소실된다. 대표적인 도형이 실험2에서 만들어 본 불가능한 도형이다.
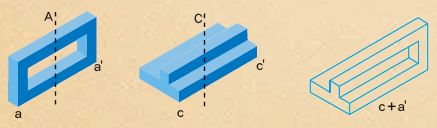
이 도형은 ‘ㅁ’자 모양의 입체도형과 ‘ㅗ’자 모양의 입체도형을 각각 반으로 자른 뒤, 두 도형의 왼쪽 부분과 오른쪽 부분을 바꾸어 붙인 것이다. 이 도형은 2차원에서만 구현 가능하며, 3차원에서는 끊어진 형태로만 나타낼 수 있다.
한편 우리는 실험1을 통해서 하나로 이어진 펜로즈 계단을 만들었다. 어떻게 된 걸까?
완성된 계단을 유심히 살펴보자, 계단을 위에서 바라보면 가장 높은 부분이 없고, 왼쪽 방향으로 계속 올라가게 된다. 그런데 계단을 아래에서 위로 바라보면 일부 계단의 바닥면이 기울어져 있다. 즉 계단의 일부를 변형해 모두 하나로 이어져 있는 펜로즈 계단을 만든 것이다. 스기하라 교수는 완벽한 펜로즈 계단은 아니지만 3차원에서도 하나로 이어진 펜로즈 계단을 만들기 위해 이 같은 방법을 사용했다.











