d라이브러리

“덜덜덜 알았어. 윷놀이고 뭐고 추워 죽겠네. 엄마, 언제 집에 가요? 너무 추워요!”
“그러게, 모자도 쓰고 목도리도 하라고 했지! 아빠 모자라도 쓰렴.”
“어? 아빠, 모자 끝에 손잡이가 있어요. 이거 뭐예요?”
“클라인병 모자란다. 뫼비우스 띠 두 개를 붙인 거지. 이참에 집에 가서 뫼비우스 모자와 클라인병을 만들어 볼까?”
“아빠, 엄마, 누나. 윷놀이는 끝내고 가야죠!”


수학자의 겨울 필수품, 뫼비우스 띠

한낮에 기온이 영하 10°를 밑돌아 뼛속까지 추운 겨울에는 모자와 목도리가 필수품이다. 그런데 수학자들은 멋을 내기 위해서 조금 특별한 목도리와 모자를 개발했다. 바로 뫼비우스 띠의 성질을 갖는 목도리와 모자다.

목도리 중에는 끝이 서로 연결되어 있는 ‘넥 워머’가 있다. 보통은 동그란 원 모양이지만, 어떤 것은 중간이 한 번 꼬아져 있어 뫼비우스 띠와 같은 구조를 가진다. 다른 모양으로 넥 워머를 만들지 않아도 자연스럽게 예쁜 모양으로 만들어져 인기가 많다.

여기서 뫼비우스 띠는 종이 띠를 한 번 꼬아 이어 붙인 것으로, 안과 밖의 구별이 없다. 독일의 수학자 아우구스트 페르디난트 뫼비우스가 1858년 발견했다.

겨울에 쓰는 털모자 끝에는 동그란 방울이 달려 있다. 그런데 수학자들은 방울이 달려 있는 대신, 모자 끝이 다른 부분과 연결되어 있는 모자를 쓰곤 한다. 즉 털모자 끝이 클라인병 구조이기 때문에 손잡이 모양처럼 되어 있다.

클라인병은 독일의 수학자 펠릭스 클라인이 고안한 것으로, 뫼비우스 띠의 성질을 그대로 유지하면서 한 차원 높은 공간에서 존재한다. 즉 뫼비우스 띠가 3차원의 도형을 2차원으로 나타낸 것이라면, 클라인병은 뫼비우스 띠의 성질을 가지는 4차원의 도형을 3차원으로 표현한 것이다. 또 클라인병은 내부와 외부의 구분이 없이 단 하나의 면으로만 이루어져 있다. 이 때문에 어느 지점에서 출발하더라도 곡면 전체를 따라가다 보면 끝없이 이어진다.

아하! 실험 플러스 뫼비우스 띠로 이루어진 클라인병

클라인병은 직사각형에서 시작됐다. 직사각형을 둥글게 말면 밑면과 윗면이 뚫려 있는 원기둥이 된다. 이 원기둥의 길이를 늘인 뒤 한쪽 끝이 원기둥의 옆면을 뚫고 들어가게 한다. 뚫고 들어간 쪽의 끝이 다른 쪽과 만나게 하면 클라인병이 된다.
 
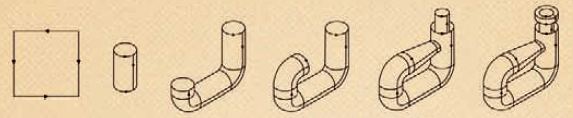
클라인병을 반으로 자르면 뫼비우스 띠 2개를 얻을 수 있다. <;실험2>;에서 만든 클라인병을 병의 손잡이가 오른쪽으로 오게 놓은 뒤, 가로축을 기준으로 똑같이 나눠 보자. 그러면 각각의 단면이 한 번 꼬아진 뫼비우스 띠임을 알 수 있다. 실제로 클라인병은 여러 개의 뫼비우스 띠로 구성돼 있다.

사실 뫼비우스 띠는 띠를 몇 번 꼬았느냐에 따라 결정된다. 띠를 홀수 번 꼬면 안과 밖의 구별이 없는 뫼비우스 띠가 되지만, 짝수 번 꼬면 안과 밖의 구별이 있어 뫼비우스 띠가 아니다.
 
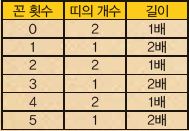
몇 번 꼬았는지에 따라 중앙선을 이등분했을 때의 띠 모양도 다르다. 꼰 횟수가 1번이면 띠의 개수는 1개이지만 길이는 2배로 늘어난다. 하지만 꼰 횟수가 2번이면 띠의 개수는 2개가 되지만 각각 띠의 길이는 그대로다. 실제로 띠를 n번 꼰 뒤 이등분하면, n이 홀수일 때 띠의 개수는 1개지만 길이는 2배가 된다. 반면 짝수이면 띠의 개수는 2개이고 길이는 그대로다.

또한 뫼비우스 띠의 가장자리를 서로 반대방향으로 이어붙이면, 보자기를 대각선으로 집어서 묶은 형태의 곡면이 생긴다. 이 곡면을 ‘사영평면’이라고 하는데, 어떤 한 지점에서 계속해서 걸으면 어느새 좌우가 바뀌는 성질을 가지고 있다. 이런 특이한 수학적 성질은 사영기하학이란 학문으로 발전되어 현대수학의 발전에 도움을 주고 있다.