“뭐야? 눈을 돋보기로 관찰하니까 완전 다른 모양이네! 거기다 모두 대칭이야~. 그래서 아름다운가?”
“우리 두리가 잘 아는구나. 그런데 눈결정보다 더 아름다운 대칭 도형이 있단다. 한 번 만들어 볼래?”
대칭에 매료된 수학자, 새로운 도형을 만들다
김태희, 이민정, 송혜교의 공통점은? 얼굴 좌우가 거의 완벽하게 대칭이라는 점이다. 대칭은 오래 전부터 아름다움의 조건이었다. 실제로 얼굴과 몸매가 좌우 대칭인 이성에게 사람들은 더 매력을 느낀다는 연구 결과가 있다. 따라서 대칭은 오래전부터 사람들의 관심 대상이었다.
수학자들도 예외는 아니었다. 수학자들의 대칭 연구는 고대 그리스 시대까지 거슬러 올라간다. 기원전 500년 경 피타고라스 학파의 수학자 테아이테토스가 정다각형으로 이루어진 입체도형을 작도하면서 시작됐다. 결국 그는 대칭을 이용해 정육면체와 정이십면체를 처음 발견하는 성과를 거두었다. 이처럼 대칭적 성질을 이용해 새로운 도형을 발견해 내는 것도 대칭 연구 중 하나다.
1970년대 미국의 수학자 앨런 홀든은 구멍 뚫린 정다각형이 일정한 규칙을 가지고 뒤엉켜 있는 모양의 새로운 도형을 만들었다. 일명 ‘오더리 탱글스(Orderly Tangles)’다.
홀든은 테아이테토스가 그랬던 것처럼 정다각형으로 이루어진 새로운 도형을 만들고 싶었다. 그래서 정다각형에 구멍을 뚫은 뒤 일정한 규칙을 갖도록 도형을 결합했다. 홀든은 여러 번의 시도 끝에 정삼각형 4개에 구멍을 뚫어 서로 엇갈리게 결합하면 새로운 도형이 만들어진다는 것을 밝혀냈다.
현재 오더리 탱글스는 수 십여 종류가 개발돼 있다. 그런데 오더리 탱글스에 매력에 빠진 건 수학자뿐만이 아니다. 정다각형이 규칙적으로 엉켜 있는 모습에 반한 디자이너들이 디자인에 활용하기 위해 오더리 탱글스를 손쉽게 만들 수 있는 소프트웨어를 개발해 사용하고 있다. 또 퍼즐전문가들도 오더리 탱글스에서 아이디어를 얻어 각종 퍼즐을 개발해 냈다.


아하! 실험!
오더리 탱글스의 수학적 성질
언뜻 보기에는 마구잡이로 뒤엉켜 있는 것 같지만, 오더리 탱글스는 모든 조각이 하나로 결합하기 위해 일정한 규칙에 따라 엉켜 있다.
예를 들어 <;실험2>;에서 빨간색 막대풍선 2개를 결합하기 위해 2개의 보라색 막대풍선은 서로 정반대의 방법으로 고리를 만들었다. 왼쪽의 보라색 풍선으로 앞에 놓인 빨간색 막대풍선부터을 먼저 걸고, 뒤에 놓인 풍선을 걸어 고리를 만들었다. 반대로 오른쪽 보라색 풍선으로는 뒤에 놓인 것을 먼저 걸고 앞에 놓인 풍선을 걸어 고리를 만들었다. 노란색 막대풍선도 마찬가지다. 2개의 막대풍선이 서로 정반대로 빨간색과 보라색 막대풍선을 걸어 고리를 만들었다.
이런 규칙을 유심히 살펴보면 수학적 성질을 발견할 수 있다. <;실험1>;을 통해 완성한 오더리 탱글스를 살펴보면서 수학적 성질을 확인해 보자
사실 <;실험1>;의 안쪽 삼각형의 한 변의 길이는 바깥쪽 삼각형의 한 변의 길이의 $ \frac{1}{2} $이다. 하지만 꼭 이와 같은 길이의 비를 갖지 않아도, 구멍 뚫린 정삼각형으로 이루어진 오더리 탱글스를 만들 수 있다. 그 경우 오른쪽의 조건을 모두 만족한다.
오더리 탱글스는 정오각형으로도 만들 수 있다. 수학동아 홈페이지(math.dongascience.com) 공지사항 게시판에서 도형 전개도를 내려받은 뒤, 오더리 탱글스를 만들어 보자. 그리고 그 안에 숨어 있는 수학적 성질을 찾아보자. 퍼즐을 푸는 재미와 함께 수학자들만이 느낄 수 있는 발견의 즐거움을 느낄 수 있다.
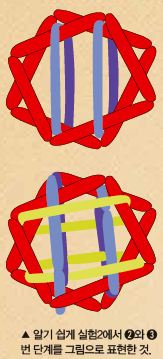
실험1 별 모양 오더리 탱글스의 수학적 성질

➊ 바깥쪽 삼각형의 변의 중점은 안쪽 삼각형의 꼭짓점과 반드시 만난다.
➋ 이 도형은 60°와 120°로만 이루어져 있다.
➌ 어느 쪽에서 봐도 같은 모양이다.