
제1코스 17공포증에 빠진 이탈리아
서양에서는 일반적으로 숫자 13을 피하거나 두려움의 대상으로 삼는다고 알려져 있다. 그런데 특이하게도 이탈리아에서는 17이라는 숫자를 피한다. 그 이유는 17의 표기법과 관련이 있다.
17을 로마숫자로 나타내면 XVII가 되는데, 이 문자의 배열을 바꾼 VIXI는 라틴어로 ‘I lived’라는 의미다. 즉, ‘나는 살았었다’로 결국 ‘나는 죽었다’는 뜻이다. 이 때문에 이탈리아에서는 17을 죽음을 상징하는 불길한 숫자로 여기고, 관련된 것은 되도록 피한다.
예를 들어, 이탈리아의 빌딩이나 호텔에서는 17층이라고 쓰지 않는다. 방의 호실도 16호, 16b호, 18호라고 배정한다. 또한 비행기 좌석 번호에 17을 쓰지 않는 항공사도 있고, 17일에는 특별한 축제를 열지 않는다.
게다가 17은 축구를 좋아하는 이탈리아인들에게 또 다른 악몽의 대상이기도 하다. 1990년 이탈리아에서 열린 월드컵 4강전에서, 홈 경기라는 이점에도 불구하고 아르헨티나를 맞아 승부차기에서 지며 결승에 진출하지 못한 것이다. 이때 승부차기에서 결정적인 실축을 한 이탈리아 선수의 등번호가 17이었으며, 아르헨티나가 선제골을 성공한 시간은 경기 시작 후 17분 뒤였고, 이날 경기는 이탈리아 대표팀이 상 파울로에서 가진 17번째 경기였다.
자국에서 열린 월드컵에서 좌절을 겪은 이탈리아인들에게 17은 더욱 부정적인 이미지 의 숫자가 됐고, 이후로도 이탈리아 축구에서 등번호 17은 기피의 대상으로 남아 있다.

제2코스 쌍둥이와 페르마의 소수, 17
17은 7번째 소수이자, 19와 함께 네 번째 쌍둥이 소수다. 또한 페르마 소수이기도 하다. 먼저 쌍둥이 소수에 대해 알아보자. 쌍둥이 소수란 두 수의 차가 2인 소수의 쌍, 즉 (p, p+2)인 소수의 쌍을 말한다. 그런데 2를 제외한 짝수 2k는 1, 2, 2k가 약수이므로, 약수의 개수가 3개 이상이 돼 소수가 될 수 없다. 따라서 2를 제외한 모든 소수는 홀수이고, (2, 3)을 제외한 두 소수의 차는 아무리 작아도 2 이상이 된다. 따라서 차가 2인 두 소수, 즉 쌍둥이 소수는 다른 말로 하면 ‘연속한 두 홀수가 모두 소수’인 경우를 말한다.

그렇다면 쌍둥이 소수는 소수처럼 무한히 많을까? 수학자들은 소수처럼 쌍둥이 소수도 무한히 많을 것이라고 예상한다. 하지만 이에 대한 증명은 아직 없다. 다만 쌍둥이 소수가 소수보다는 훨씬 적을 것이란 예상은 할 수 있는데, 이것은 ‘오일러의 정리’와 ‘브룬의 정리’로 알 수 있다.
18세기 스위스의 수학자 레온하르트 오일러는 소수의 역수의 합이 무한대라는 것을 이용해 소수가 무한하다는 사실을 증명했다.

오일러의 아이디어는 ‘소수의 개수가 유한하다면 그 역수의 합은 무한대가 아니어야 하는데, 소수의 역수의 합이 무한하므로 소수는 무한히 많다’는 것이다.
그런데 1915년 노르웨이의 수학자 비고 브룬은 ‘쌍둥이 소수의 역수의 합이 약 1.90216’이라는 것을 밝혔다. 그는 이 값에 자신의 이름을 붙여 ‘브룬 상수’라고 이름지었다.
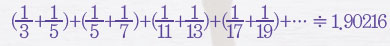
물론 1+1/2+1/2²+1/2³+…=2와 같이 무한히 많은 수들의 합도 무한대가 아닐 수 있으므로, 쌍둥이 소수의 역수의 합이 무한대가 아니라고 해서 그 개수가 유한하다고 말할 수는 없다. 하지만 두 가지 사실로부터 소수 중 쌍둥이 소수를 제외한 역수의 합은 무한대고, 쌍둥이 소수가 소수에서 차지하는 비중이 상대적으로 낮다는 것을 알 수 있다.

제3코스 의외로 작도가능한 정17각형

눈금 없는 자와 컴퍼스만을 이용하여 어떤 도형을 그리는 것을 ‘기하학적 작도’라고 한다. 자와 컴퍼스처럼 단순한 도구로 얼마나 작도할 수 있을지 의구심도 들지만, 생각보다 많은 다각형을 작도할 수 있다.
하지만 자와 컴퍼스만 갖고는 아무리 해도 작도가 되지 않는 다각형도 있다. 자와 컴퍼스만으로 작도하는 문제 중 가장 유명한 것은 고대 그리스에서 전해져 온 ‘삼대 작도 문제’다.
고대 그리스 시대부터 수많은 사람들이 아래의 3가지 도형을 작도하는 것에 도전해 왔지만, 성공을 거두지 못했다. 그러다 19세기에 이르러서야 비로소 이 도형들은 작도가 불가능하다는 것이 수학적으로 증명됐다.
1. 주어진 정육면체보다 부피가 두 배인 정육면체
2. 임의의 각을 삼등분한 각
3. 주어진 원과 넓이가 같은 정사각형
3대 작도 문제와 더불어 오랫동안 많은 수학자들의 관심을 받은 ‘작도 가능한 정n다각형에는 어떤 것들이 있는가?’이다. 정n각형 중 정삼각형과 정사각형, 정오각형, 정육각형은 작도가 가능하다. 하지만 정7각형, 정9각형, 정11각형, 정13각형, 정17각형 등을 작도할 수 있는지는 오랫동안 풀리지 않았다. 이 중에서도 특히 정7각형과 정17각형의 작도 문제는 많은 수학자들의 골칫거리였다.


따라서 정17각형은 작도하는 과정이 결코 간단하지는 않더라도 작도가 가능한 도형이다. 또한 가우스는 정17각형뿐만 아니라 n이 페르마 소수이면 정n각형은 작도가 가능하다는 것까지 증명했다.
가우스는 자신의 이 업적을 매우 자랑스럽게 여겨서, 수학자 아르키메데스나 베르누이가 묘비에 자신의 업적을 새긴 것처럼 자신도 묘비에 정17각형을 넣어 주기를 원했다. 하지만 정17각형을 그림으로 나타내면, 원과 거의 구분이 되지 않기 때문에 가우스의 묘비에는 점 17개를 연결한 별 모양을 새겨 넣었다고 전
해진다.
비록 그의 묘비에 정17각형은 없지만, 가우스의 고향에 세워진 그의 동상 받침대 모양은 그의 업적을 기려 정17각형 모양으로 만들어졌다.

이탈리아인들에게 17은 공포의 대상이지만, 17년 매미에게 17은 생존 전략이다. 또한 17은 소수 중
에서도 쌍둥이 소수와 페르마 소수로서 특별한 의미를 담고 있다. 특히 17이 페르마 소수라는 점은
가우스가 정17각형을 작도 가능한 도형이라고 증명한 것과 밀접한 관련이 있다.
우리가 미처 발견하지 못한 17의 매력은 또 없을까? 17 속에는 아직도 숨은 매력이 있을지 모른다. 10월엔 17의 매력을 발견하는 일에 매진해 보는 것은 어떨까?











