d라이브러리

이번 호에서는 중학수학의 꽃인‘삼각비’를 살펴보도록 해요. 삼각비에 대한 처방전은 인하대학교 사범대학 부속중학교 김도훈 선생님께 받아왔습니다. 김도훈 선생님은 올해로 7년째 학생들과 수학으로 소통하고 계세요. 2011년부터 교내 수학·과학 영재 심화반을 담당하시고, 현재 전국수학교사모임의‘셈사랑’이라는 세미나 팀에서 활동 중이시죠. 김 선생님은‘셈사랑’선생님들과 함께 지난 11월,국립과천과학관에서 열린 제1회 수학문화축전에서 수학 독서를 주제로 한 수학전시회를 열기도 하셨어요. 뛰어난 유머감각 덕분에 선생님의 수업은 언제나 웃음이 끊이지 않는다고 해요. 오늘은 특별히기말고사 이후에도 쉬지 않고 수학 공부를 이어가고 있는 인하사대부중 3학년 학생들 6명과 함께했습니다.



선생님,‘삼각비’는 왜 배워야 하죠?

삼각비는 직각삼각형의 세 변의 길이에 대한 비를 공부하는 단원입니다. 초등학교 5학년 때 배웠던 ‘비와 비례식’ 단원과, 중학교 2학년 때 배웠던‘닮음’단원이 동시에 활용되는 단원이기도 해요. 왼쪽 그림❶과 같은 삼각형 ABC를 살펴보며 삼각비에 대해 자세히 이야기 할게요.
 

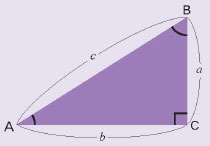
삼각형 ABC는 두 개의 예각(∠A, ∠B)과 한 개의 직각(∠C)으로 돼 있습니다. 모든 직각삼각형은 한 예각의 크기가 같으면 서로 닮음이 되는 성질이 있죠. 삼각비는 이 성질을 활용하는 단원입니다. 직각삼각형의 한 예각에서 만나는 두 변의 길이의 일정한 비를 삼각비라고 하는 것이죠.

이와 같은 삼각비의 성질을 활용하면 우리가 직접 잴 수 없는 거리나 높이, 삼각형의 넓이 등을 구할수 있어요. 12쪽 화이트보드에 적힌‘63빌딩의 높이를 구하는 문제’를 보면서 설명해 줄게요. 그림❷를 함께 살펴보면 쉽게 이해할 수 있을 거예요.
 

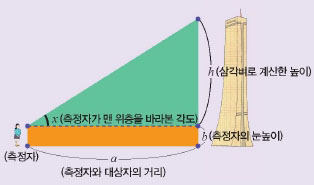
먼저 측정자는 건물과 일정한 거리를 유지하고 건물 앞에 바로 섭니다. 그 자리에서 건물의 맨 위층을 바라볼 때의 각도를 재고, 거리정보와 각도정보를 이용해 삼각비 구하면 문제를 풀 수 있죠. 이 때는 탄젠트를 이용해요. tan x =h/a이고 h=atanx이므로, 거리정보(a)와 각도정보(x)를 각각 대입하면 됩니다. 아차! 이 공식을 이용해 구한 높이(h)는 측정자의 눈높이에서 시작한 건물의 높이이므로, 실제 높이는 삼각비로 계산한 높이(h)에 측정자의 눈높이(b)를 더해야 해요.

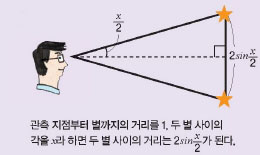
삼각비는 고대 그리스의 천문학자들이 처음 연구했어요. 그들은 두 별 사이의 거리를 정확히 측정하는 일에 집중했는데, 이 때 삼각비를 활용한 거예요. 모든 별들이 하나의 구면 위에 높여 있다고 생각하고, 두 별사이의 각도를 쟀어요. 측정한 각도를 이용해 아래 그림❸과 같이 삼각형을 만들고 삼각비를 이용해 두 별 사이의 거리를 예측할 수 있었답니다.
 

선생님만 알고 있는 비밀

● 선생님, 삼각비 용어가 헷갈려요!

사실 직각삼각형에서 두 변의 길이를 이용한 비는 사인, 코사인, 탄젠트를 포함해 여섯 종류가 있어요. 이 중에서 중학교에서는 세 가지(사인, 코사인, 탄젠트)만 배우죠. 나머지는 이들의 역수에 대한삼각비인데, 이것은 고등학교 과정에서 배워요. 그렇기 때문에 삼각비를 처음 배울 때 개념을 정확히이해하는 것이 중요합니다. 사인, 코사인, 탄젠트의 유래를 듣고 나면 낯선 느낌이 조금 줄어들 거예요.
 

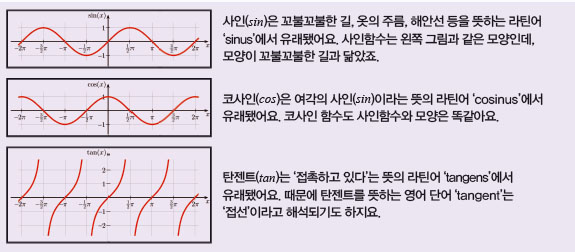
이제부터라도 삼각비의 새로운 용어를 무작정 외우기보다는 그 유래와 삼각함수 그래프를 떠올리며 기억해 보길 추천합니다.

김도훈 선생님의‘삼각비’정복 비법 전수!

삼각비를 정복하려면 가장 먼저 사인, 코사인, 탄젠트가 어떤 각의 비를 이야기 하는지 정확히 알아야 해요. 이 때 각 A에 대한 sin A, cos A, tan A라는 것도 절대 잊지 말고요!
 

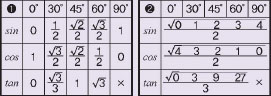
‘특수각에 대한 삼각비’는 반드시 암기해야 해요. 보통 교과서에는 ❶번 표를 공개하죠. 하지만 ❷번 표와 같은 방법으로 새롭게 외워 보는 것은 어떨까요? 특수각의 크기에 따라 일정한 규칙이 있으니, 좀 더 쉽게 외울 수 있을 거예요. 또한 삼각비를 계산하는 문제에서 꼭 기억해야 하는 부분이 있어요.
 

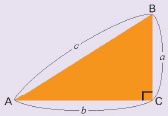
예를 들어 ‘왼쪽 그림을 보고 sinA 값을 구하라’는 문제를 풀어 봅시다. 이 때 sinA 값은 a/c로 구할 수 있는데, 학생들은 마치 이 식이 모든 사인 값을 구하는 공식인 것처럼 착각할 때가 있어요. 선생님들이 가끔 함정을 만들기 위해 그림을 바꾸지 않고, sinB 값을 구하라는 문제를 내거든요. 이 때 많은 학생들이 sinB의 값 마저도 a/c를 이용해 틀리곤 하지요. 때문에삼각비 문제를 풀 때는 어떤 예각의 사인 값을 구하라고 하는 문제인지를 꼼꼼히 읽어야 해요. 문제를 한 번 더 살피면 실수를 더욱 줄일 수 있답니다!

초등학교 과정에서는 기호를 배우지 않기 때문에 중학생이 되어서도 기호를 불편해 학생들이 많습니다. 삼각비 단원이 어렵게 느껴지는 이유도 기호 때문일 수 있어요. 그렇지만 지금까지 살펴본 내용만 잘 기억한다면 삼각비 정복은 문제없어요. 여러분 모두 수학을 정복해서 자신의 꿈에 한 발 더 다가서길 바랄게요!