d라이브러리

태국에서 홍수가 났다. 조금 먼 얘기지만 우리 생활에 큰 영향을 끼쳤다. 10월말 갑자기 하드디스크 값이 두 배 이상 올랐고 덩달아 컴퓨터 가격도 올라갔다. 원인은 태국에 큰 홍수가 나 하드디스크 공장이 잠겼기 때문이다. 멀리 동남아시아의 일이지만 우리와 밀접한 관련이 있다. 이런 홍수를 수학이막을 수 있다고 한다. 어떻게 가능할까.


태국 홍수가 일어난 이유는?

태국말로‘남 뚜엄’이라 불리는 홍수는 지난 7월 말부터 11월 초까지 내린 비 때문에 일어났다. 태국의 북부 산악지대에서 시작해 방콕을 거쳐 타이 만으로 흐르는, 우리나라의 한강격인 짜오프라야 강이 넘쳤기 때문이다. 수백 명의 사망자와 300만 이상의 수재민, 50억 달러에 달하는 피해가 발생했고 피해는 앞으로 더 커질 전망이다. 태국의 수도 방콕에서도 우리나라의 김포공항격인 ‘돈무앙’공항은 물론 왕궁까지 물에 잠겼다.

사실 태국에서는 기후와 지형 때문에 홍수가 자주 일어난다. 태국은 열대 몬순 기후로 5월부터 10월까지 비가 많이 온다. 지형이 완만해 물이 빠져 나가는 속도가 느린데 물이 흐르는 속도보다 빨리 비가 내려 홍수가 일어난 것이다. 하지만 올해의 홍수는 매년 일어난 홍수에 비해 규모와 피해 정도가 컸다. 50년 만에 큰 비가 내렸기 때문이다. 태국은 보통 연평균 강수량이 1000mm정도지만, 올해는 10월말까지 1500mm 넘게 내렸다. 그리고 물이 방콕 인근으로 내려왔을 무렵 *만조가 겹쳐 홍수가 더 커졌다.

그런데 이런 자연적 이유 말고도 다른 중요한 이유가 있다. 태국에 댐과 같은 홍수를 막을 수 있는 시설이 제대로 갖춰져 있지 않았다는 점이다. 태국의 댐은 대부분 한해에 비가 1000mm 내리는 것을 생각하고 지어 1500mm의 비를 견딜 수 없다. 1L짜리 컵에 1.5L의 물을 넣으니 넘친 것이다.

댐을 적절히 관리하지도 못했다. 태국은 보통 10월부터 다음해 5월까지 비가 거의 오지 않는다. 태국은 논농사를 많이 짓기 때문에 10월부터 댐에 물을 가득 채워 물이 부족한 시기를 견딘다. 하지만 올해는 예년과 달리 비가 그치지 않고 계속 내렸다. 댐에 담을 수 있는 물보다 많은 비가 내리니, 여러 댐들이동시에 물을 마구 하류로 쏟아 버리기 시작했고, 이 강물과 비가 모여 한꺼번에 평탄한 태국의 남부로 내려와 큰 홍수가 일어난 것이다.
 

홍수 막는 수학 1. 물의 양을 알면 백전백승

홍수를 막기 위해선 규모가 큰 댐이 필요하다. 댐은 생활에 필요한 물을 저장해뒀다 공급하기도 하고,전기를 만들기도 한다. 또 다른 중요한 기능은 홍수를 조절하는 능력이다.

비가 많이 오면 댐은 물을 잠시 막아 하류에서 물이 넘치는 것을 막는다. 비가 더 이상 오지 않는다고 해서 모아둔 물을 바로 내려보내지는 않는다. 갑작스럽게 많은 물을 내려 보내면 위험하기도 할 뿐더러, 가물 때 쓸 물이 부족할 수도 있기 때문이다. 그런데 홍수를 막으면서 물을 안정적으로 공급하기는 쉽지 않다. 비가 많이 올 때 지나치게 댐의 수위를 낮추면 가물 때 물이 부족하게 되고, 반대로 비가 안 올 때 수위를 높이면 홍수 때 물을 담아 둘 수가 없다.

이런 어려움을 해결하는 첫 번째 방법은 물의 양을 철저히 계산하는 것이다. 먼저 비의 양과 강물의 높이의 관계를 정확히 알아야 한다. 그래서 강을 관리할 때는 이 둘 사이의 관계를 수학적 그래프로 알아 낸다. 이를 표현한 것이 수문 곡선이다.
 

수문곡선
 

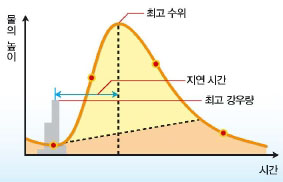
왼쪽의 회색 막대그래프는 강수량이다. 비가 온 뒤 일정한 시간이 지나야 하천의 수위가 높아진다. 이 시간은 강마다 각각 다른데, 이 그래프를 통해 비가 온 것이 언제 강의 높이에 반영되는지를 알 수 있다.

그래프 위쪽의 노란색은 비가 와서 높아진 수위다. 빗물이 몰려들면서 갑작스레 수위가 높아졌다가, 최고점을 찍고 점점 낮아진다. 아래쪽의 주황색은 원래 강에 흐르고 있던 물의 높이로, 천천히 높아졌다가 조금 늦게 원래의 수위를 되찾는다. 이 그래프는 비가 온 양과 유역의 크기 등에 따라 높이와폭이 달라진다. 이런 수문 곡선을 이용하면 비가 올 때 한 지점에서 시간에 따른 강물의 변화를 알아낼 수 있다.


홍수 막는 수학 2. 한꺼번에 물 몰리면 큰일

이 곡선을 토대로 댐이 담당하는 유역에 내린 비와 앞으로 내릴 비의 양의 합(I), 댐에서 보관할 수 있는 양(S)을 계산해 하류로 내보낼 물의 양(O)을 결정(I-O=S)한다.

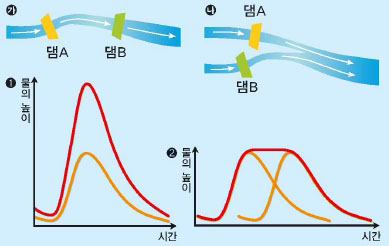
물을 내보낼 때는 하류에 끼칠 영향과 다른 댐도 생각해야 한다. 강에는 여러 댐이 있어 서로 내보낸물에 의해 하류가 영향을 받기 때문이다. 만약 강에 댐 두 개가 일렬로 있다면(가), 상류의 댐 A에서는 하류의 댐 B의 수위와 날씨를 고려한다. 하류 지역에 많은 비가 내려 댐 B의 수위가 높을 때는 댐A에서 물을 보내면 안 되기 때문이다. 댐 B의 수위가 가장 높아질 때와 보낸 물이 겹치면 최악의 경우 댐 B가 무너질 수도 있다.

양 갈래로 나뉜 물이 하나로 합류하는 강(나)은 댐을 관리하기가 더 어렵다. 만약 상류의 두 강에 댐A와 댐 B가 각각 있을 때, 두 댐이 동시에 방류하면 큰 홍수가 날 수 있다. 이 두 댐이 동시에 하류의 도시에 도달하게끔 물을 내보내면 중첩된 엄청난 물이 도시로 몰려온다(①). 따라서 한쪽을 조금 늦거나 빠르게 방류해야 한다(②). 실제로 우리나라에선 홍수통제소가 이런 수학적 원리를 이용해 댐을 관리한다. 하지만 태국은 이렇게 댐을 관리하는 곳이 없어 피해를 키웠다.
 

홍수 막는 비결은 수학

홍수를 막으려면 이런 계산과 동시에 정확한 날씨와 강우량 예측이 필요하다. 앞으로 내릴 비의 양에따라 댐의 수위를 조절할 수 있기 때문이다. 날씨를 예측하는 것도 수학적으로 만든 모델을 사용한다.수치예보 모델은 기온, 기압, 바람, 수증기 같은 기상 요소가 시간에 따라 어떻게 변하는지를 방정식으로 표현한 것 이다. 육지와 해상, 상공에서 기상장비로 측정한 자료를 계산하면 미래 대기 상태를 예측할 수 있다.
결국 홍수를 막기 위해선 수치를 통한 정확한 기상 예측과 강의 관리가 필요하다. 태국에서 자주 일어나는 남 뚜엄을 막는 비결은 바로 수학에 있다.


*만조는 밀물이 가장 높이 들어오는 현상을 말한다.