
두 공주는 마녀가 설계한 새로운 실험에 참여하기로 했다. 왕자는 이번에도 일요일 밤에 동전을 던져 결과에 따라 다른 방식으로 공주를 깨운다.
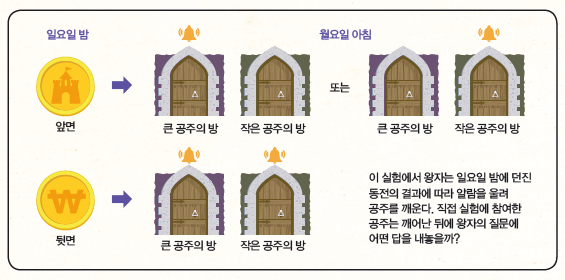
먼저 큰 공주와 작은 공주가 일요일 밤에 각기 다른 방에서 잠든다. 이들은 실험이 끝날 때까지 서로 대화할 수 없으며, 상대방이 어떤 상태인지 전혀 모른다. 이들이 잠든 뒤 왕자는 동전을 던진다. 물론 이 동전은 앞면이 나올 확률과 뒷면이 나올 확률이 똑같다.
일요일에 던진 이 동전이 앞면이 나올 경우, 왕자는 월요일 아침에 큰 공주와 작은 공주 가운데 임의로 한 사람을 뽑아 깨운다. 동전이 뒷면이 나올 경우, 월요일 아침에 큰 공주와 작은 공주 모두를 깨운다. 왕자가 깨우기 전에 공주가 먼저 깨어나는 일은 없다.
왕자는 깨어나는 공주에게 이렇게 묻는다. “제가 일요일에 던진 동전이 앞면이 나왔을 확률은?” 잠에서 깬 공주는 왕자의 질문에 뭐라고 답해야 할까? 단, 질문을 받는 공주는 다른 공주도 질문을 받는지 알 수 없다.
큰 공주와 작은 공주 중 누구든 잠에서 깨어나면 ‘일요일에 왕자가 던진 동전이 앞면이 나왔고 공주 둘 중에 자기 자신만 깨어난 상황’과 ‘왕자가 던진 동전이 뒷면이 나와서 실험에 참여한 공주가 모두 깨어난 상황’ 중 지금이 어느 경우에 해당하는지 고민할 것이다. 어떤 경우에도 다른 공주의 상태를 알 수 없기 때문에 동전이 앞면이 나왔을 확률을 계산하기가 쉽지 않다. 잠에서 깬 공주는 ‘내가 깨어났다’는 정보와 아래 세 가지 당연한 명제만으로 확률을 계산해야 한다.
먼저 큰 공주와 작은 공주가 일요일 밤에 각기 다른 방에서 잠든다. 이들은 실험이 끝날 때까지 서로 대화할 수 없으며, 상대방이 어떤 상태인지 전혀 모른다. 이들이 잠든 뒤 왕자는 동전을 던진다. 물론 이 동전은 앞면이 나올 확률과 뒷면이 나올 확률이 똑같다.
일요일에 던진 이 동전이 앞면이 나올 경우, 왕자는 월요일 아침에 큰 공주와 작은 공주 가운데 임의로 한 사람을 뽑아 깨운다. 동전이 뒷면이 나올 경우, 월요일 아침에 큰 공주와 작은 공주 모두를 깨운다. 왕자가 깨우기 전에 공주가 먼저 깨어나는 일은 없다.
왕자는 깨어나는 공주에게 이렇게 묻는다. “제가 일요일에 던진 동전이 앞면이 나왔을 확률은?” 잠에서 깬 공주는 왕자의 질문에 뭐라고 답해야 할까? 단, 질문을 받는 공주는 다른 공주도 질문을 받는지 알 수 없다.
큰 공주와 작은 공주 중 누구든 잠에서 깨어나면 ‘일요일에 왕자가 던진 동전이 앞면이 나왔고 공주 둘 중에 자기 자신만 깨어난 상황’과 ‘왕자가 던진 동전이 뒷면이 나와서 실험에 참여한 공주가 모두 깨어난 상황’ 중 지금이 어느 경우에 해당하는지 고민할 것이다. 어떤 경우에도 다른 공주의 상태를 알 수 없기 때문에 동전이 앞면이 나왔을 확률을 계산하기가 쉽지 않다. 잠에서 깬 공주는 ‘내가 깨어났다’는 정보와 아래 세 가지 당연한 명제만으로 확률을 계산해야 한다.

★공주의 주장
실험에 참여한 내가 잘 알지!

“공주님, 일어나세요. 그리고 제가 일요일에 던진 동전이 앞면이 나왔을 확률을 말해보세요.”
왕자가 저를 깨우는 목소리가 들립니다. 잠들기 전에 실험 과정에 대해 익히 들었기 때문에 지금부터 논리적으로 답을 구해보겠습니다.
왕자가 동전을 던지면 월요일에 적어도 한 명은 잠에서 깨어납니다. 그리고 큰 공주인 제가 깨어났어요. 이때 제가 계산한 동전이 앞면이 나왔을 확률은 아래와 같습니다.
왕자가 저를 깨우는 목소리가 들립니다. 잠들기 전에 실험 과정에 대해 익히 들었기 때문에 지금부터 논리적으로 답을 구해보겠습니다.
왕자가 동전을 던지면 월요일에 적어도 한 명은 잠에서 깨어납니다. 그리고 큰 공주인 제가 깨어났어요. 이때 제가 계산한 동전이 앞면이 나왔을 확률은 아래와 같습니다.

‘큰 공주가 잠들기 전에 계산한, 자신이 월요일에 깨어날 확률’은 조건부 확률에 의해 3/4입니다. 같은 방법으로 작은 공주가 잠들기 전에 계산한, 작은 공주 자신이 월요일에 깨어날 확률도 3/4입니다.

그러므로 큰 공주인 제가 월요일에 깨어나 계산한, 동전이 앞면이 나왔을 확률은 1/4÷3/4= 1/3입니다. 마찬가지로 만약 월요일에 깨어난 사람이 작은 공주라면, 작은 공주가 깨어나 계산한 동전이 앞면이 나왔을 확률도 1/3입니다. 저는 정답이 1/3이라고 확신한답니다! 제 논리에 결함은 없을 걸요?
★마녀의 주장
잠에서 깼다는 걸 어떻게 알았지?
실험에 참여하지는 않았지만 나 또한 실험을 지켜보며 공주가 뭐라고 답해야 할지 계산해 봤어. 그런데 공주의 주장에는 허점이 있다고! 내 이야기를 한번 들어봐.
월요일 아침, 나도 누가 깨어났는지 알기 전까지는 동전이 앞면이 나왔을 확률이 1/2이라고 생각했지. 왕자가 “큰 공주가 월요일에 깨어났다”고 알려줬을 때, 공주와 똑같은 계산 방법으로 동전이 앞면이 나왔을 확률을 구해보니 1/3이 나오더군. 하지만 같은 방법으로 이 실험에 공주 여러 명이 참여하는 경우를 상상해서 문제를 풀어보니 이상한 답이 나왔지 뭐야?
이럴 때는 사실을 전해들은 절차를 의심해봐야 하지. 정보를 얻는 절차는 두 가지야. 모든 사실을 알고 있는 사람이 주관적으로 골라낸 사실을 전달받는 ‘치우친 절차’, 정보를 얻기 위해 먼저 질문하되 질문에 대한 답이 ‘아니오’일 가능성도 있는 ‘마구잡이 절차’가 있지.
누가 깨어났는지 모두 아는 왕자가 깨어난 공주 한 명이나 두 명 중 한 명을 골라 내게 알려줬기 때문에 난 치우친 절차로 정보를 얻은 거야. 만약 누가 깨어났는지 모르는 내가 큰 공주와 작은 공주 가운데 아무나 한 명을 고른 다음 왕자에게 ‘그 공주가 월요일에 깨어났는지’물어봤다면 마구잡이 절차를 따라 정보를 얻었겠지. 내가 “큰 공주가 깨어났나요?”라고 물었을때 큰 공주가 깨어나지 않았다면 왕자는 “아니오”라고 말할 것이기 때문이야.
★마녀의 주장
잠에서 깼다는 걸 어떻게 알았지?
실험에 참여하지는 않았지만 나 또한 실험을 지켜보며 공주가 뭐라고 답해야 할지 계산해 봤어. 그런데 공주의 주장에는 허점이 있다고! 내 이야기를 한번 들어봐.
월요일 아침, 나도 누가 깨어났는지 알기 전까지는 동전이 앞면이 나왔을 확률이 1/2이라고 생각했지. 왕자가 “큰 공주가 월요일에 깨어났다”고 알려줬을 때, 공주와 똑같은 계산 방법으로 동전이 앞면이 나왔을 확률을 구해보니 1/3이 나오더군. 하지만 같은 방법으로 이 실험에 공주 여러 명이 참여하는 경우를 상상해서 문제를 풀어보니 이상한 답이 나왔지 뭐야?
이럴 때는 사실을 전해들은 절차를 의심해봐야 하지. 정보를 얻는 절차는 두 가지야. 모든 사실을 알고 있는 사람이 주관적으로 골라낸 사실을 전달받는 ‘치우친 절차’, 정보를 얻기 위해 먼저 질문하되 질문에 대한 답이 ‘아니오’일 가능성도 있는 ‘마구잡이 절차’가 있지.
누가 깨어났는지 모두 아는 왕자가 깨어난 공주 한 명이나 두 명 중 한 명을 골라 내게 알려줬기 때문에 난 치우친 절차로 정보를 얻은 거야. 만약 누가 깨어났는지 모르는 내가 큰 공주와 작은 공주 가운데 아무나 한 명을 고른 다음 왕자에게 ‘그 공주가 월요일에 깨어났는지’물어봤다면 마구잡이 절차를 따라 정보를 얻었겠지. 내가 “큰 공주가 깨어났나요?”라고 물었을때 큰 공주가 깨어나지 않았다면 왕자는 “아니오”라고 말할 것이기 때문이야.

치우친 절차에 따라 알게 된 정보는 이미 던진 동전이 앞면이 나왔을 확률을 계산하는 데 영향을 주지 않아. 그 정보를 골라내는 데 타인의 주관이 끼어들었기 때문이야. 이렇게 어떤 정보를 얻었을 때, 정보를 얻은 과정과 전달받은 사람의 관점이 정보를 활용하는 데 영향을 주는 것을 ‘관찰 선택 효과’라고 해.
관찰 선택 효과는 실생활에서 종종 나타나지. 민심을 듣기위해 전화로 여론조사를 하는 경우를 예로 들어볼까? 한때 이런 방식의 여론조사는 대다수 사람들을 위한 정책을 만드는 데 활용할 수 없었어. 당시에는 부유한 사람들만 집에 전화기를 둘 수 있었기 때문이야. 전화로 직접 국민의 의견을 듣기 위해 시작했지만 결국 부유층의 의견만 반영된 거지.
그러므로 내가 ‘큰 공주가 월요일에 깨어났다’는 정보를 들은 뒤에도 동전이 앞면이 나왔을 확률은 변함없이 1/2이어야 해. 공주가 내놓은 답인 1/3이 맞으려면 실험에서 공주가 마구잡이 절차에 따라 문제를 푸는 데 필요한 정보를 얻었다는 것을 증명해야 해. 하지만 공주가 나처럼 치우친 절차에 따라 정보를 얻었다면 정답은 1/2이어야 해. 공주에게 아직 증명해야 할 부분이 남아있다는 말씀이야!
다음 이야기
확률을 사람만큼 계산할 수 있는 인공지능, 시리가 있습니다. 일요일까지 시리는 하나뿐입니다. 일요일 저녁에 멀쩡한 동전을 던져 뒷면이 나오면 월요일에 이 시리를 복제해 인공지능을 하나 더 만들기로 했습니다. 원래 있었던 인공지능을 시리 A, 복제해 만든 인공지능을 시리 B라고 하겠습니다. 만약 일요일 저녁에 던진 동전이 앞면이 나오면 월요일에도 이 세상에 시리는 시리 A하나밖에 없습니다. 본격적인 실험은 지금부터입니다. 동전을 던지기 전에 시리 A는 꺼두고, 월요일에는 시리 A든 시리 B든 존재하는 모든 시리를 켤 것입니다. 이 실험 내용은 두 시리의 내장 기억장치에 각각 저장됐으며, 언제든지 이 정보를 꺼내 확률을 계산할 때 사용할 수 있습니다. 그렇다면, 월요일에 켜진 시리는 ‘자신이 시리 A일 확률’이 얼마라고 생각해야 할까요?
관찰 선택 효과는 실생활에서 종종 나타나지. 민심을 듣기위해 전화로 여론조사를 하는 경우를 예로 들어볼까? 한때 이런 방식의 여론조사는 대다수 사람들을 위한 정책을 만드는 데 활용할 수 없었어. 당시에는 부유한 사람들만 집에 전화기를 둘 수 있었기 때문이야. 전화로 직접 국민의 의견을 듣기 위해 시작했지만 결국 부유층의 의견만 반영된 거지.
그러므로 내가 ‘큰 공주가 월요일에 깨어났다’는 정보를 들은 뒤에도 동전이 앞면이 나왔을 확률은 변함없이 1/2이어야 해. 공주가 내놓은 답인 1/3이 맞으려면 실험에서 공주가 마구잡이 절차에 따라 문제를 푸는 데 필요한 정보를 얻었다는 것을 증명해야 해. 하지만 공주가 나처럼 치우친 절차에 따라 정보를 얻었다면 정답은 1/2이어야 해. 공주에게 아직 증명해야 할 부분이 남아있다는 말씀이야!
다음 이야기
확률을 사람만큼 계산할 수 있는 인공지능, 시리가 있습니다. 일요일까지 시리는 하나뿐입니다. 일요일 저녁에 멀쩡한 동전을 던져 뒷면이 나오면 월요일에 이 시리를 복제해 인공지능을 하나 더 만들기로 했습니다. 원래 있었던 인공지능을 시리 A, 복제해 만든 인공지능을 시리 B라고 하겠습니다. 만약 일요일 저녁에 던진 동전이 앞면이 나오면 월요일에도 이 세상에 시리는 시리 A하나밖에 없습니다. 본격적인 실험은 지금부터입니다. 동전을 던지기 전에 시리 A는 꺼두고, 월요일에는 시리 A든 시리 B든 존재하는 모든 시리를 켤 것입니다. 이 실험 내용은 두 시리의 내장 기억장치에 각각 저장됐으며, 언제든지 이 정보를 꺼내 확률을 계산할 때 사용할 수 있습니다. 그렇다면, 월요일에 켜진 시리는 ‘자신이 시리 A일 확률’이 얼마라고 생각해야 할까요?

독자의 선택
잠에서 깬 공주가 왕자가 던진 동전이 앞면이 나왔을 확률이 뭐라고 해야 할지 수학동아 블로그에서 의견을 모았다. 공주는 ‘내가 잠에서 깨어났다’는 정보를 활용해 동전이 앞면이 나왔을 확률을 구했는데, 과연 ‘내가 잠에서 깨어났다’는 정보를 어떻게 알았을까? 아래 두 주장과 독자의 의견을 읽고 결국 공주의 답이 무엇이어야 할지 생각해 보자!

antoniozo님
일요일에 던진 동전이 앞면이 나왔을 확률은 (동전이 앞면이 나와 내가 깨어날 확률)÷(내가 깨어날 확률)입니다. 내가 깨어날 확률은 (동전이 앞면이 나와 내가 깨어날 확률)+(동전이 뒷면이 나와 내가 깨어날 확률)이지요.
➊ 동전이 앞면이 나와 내가 깨어날 확률)=(동전이 앞면이 나올 확률 1/2)×(두 공주 중 내가 깨어날 확률 1/2) = 1/4
➋ (동전이 뒷면이 나와 내가 깨어날 확률)=(동전이 뒷면이 나올 확률)= 1/2 따라서, 일요일에 던진 동전이 앞면이 나올 확률은1/4÷( 1/4+ 1/2)= 1/4÷3/4= 1/3입니다.
blueart3917님
정답은 1/2입니다. 만약 큰 공주가 깨어났다면 공주의 입장에서는 지금이 ‘동전이 앞면이 나와서 자신만 깨어난 경우’와 ‘동전이 뒷면이 나와서 자신과 작은 공주가 둘 다 깨어난 경우’ 둘 중 하나이기 때문입니다. 왕자가 큰 공주 자신에게 질문했다는 것은 왕자가 자신을 깨웠다는 것을 의미하므로 왕자가 자신이 아닌 다른 공주만 깨웠을 경우까지 생각할 필요는 없다고 생각합니다.












