d라이브러리

“어텐션~! 보라야! 저 팽이처럼 저렇게 빙글빙글 돌아야 한단다. 알겠니?”
“박사님 이렇게요? 넘어지지 않고 잘 도는 게 어려워요. 그런데 박사님 갑자기 발레는 왜 배우는 거예요?”
“빙글빙글 돌면 재밌는 입체도형을 만들 수 있기 때문이지. 이제 옷 갈아입고 실험실로 가 보자꾸나.”


아르키메데스의 회전체

동전을 세운 다음, 손가락으로 쳐서 동전을 회전시켜 보자. 동전이 움직이는 방향과 경로에 따라 다양한 모양이 생긴다. 만약 동전이 제자리에서 돌면 동전의 지름을 회전축으로 하는 구가 되고, 동전이 움직이면서 회전하면 가래떡 모양의 원기둥이나 튜브 모양이 된다. 이렇게 회전축을 중심으로 평면도형을 회전시키면 다양한 입체를 만들 수 있다. 이런 입체도형을 ‘회전체’라고 한다.

이제 직각삼각형, 반원, 직사각형을 회전시키면 어떤 입체도형이 될지 상상해 보자. 회전축을 무엇으로 정하느냐에 따라 다양한 모양이 얻어진다. 직각삼각형의 경우에는 높이를, 반원에서는 지름을, 직사각형에서는 긴 변을 회전축으로 정하고 회전시키면 그림 ➊~➌과 같이 각각 원뿔, 구, 원기둥이 생긴다.
 

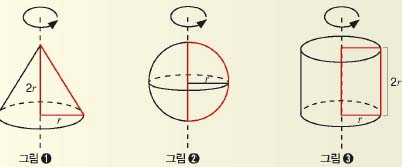
그림 ➊~➌에서 원의 반지름을 r, 그림 ➊과 ➌에서 높이 h는 2r이라고 하자. 그런 다음 원뿔, 구, 원기둥의 부피를 각각 A, B, C라 하면 그 비는 1 : 2 : 3으로 정수비가 된다.
 

이 사실에 감동한 고대 그리스의 수학자 아르키메데스는 자신이 죽을 때, 자신의 묘비에 이 내용을 새겨줄 것을 당부한 것은 수학사에 잘 알려진 유명한 일화 중 하나다. 오늘날에는 이것을 반영해 수학계 최고의 영예인‘필즈상(메달)’앞면에는 아르키메데스의 얼굴을, 뒷면에는 구와 원기둥을 상징하는 그림을 그려 넣었다.


아하! 생각이 쑥쑥! 생활 속의 회전체

요즘 프로야구에 대한 열기가 뜨겁다. 야구방망이로 공을 때려 외야 펜스를 넘기는 홈런은 여름의 뜨거움을 식힐 만큼 시원하다. 타자가 쥐고 있는 야구방망이는 회전체다. 야구방망이를 긴 방향에 수직으로 자르면 그 단면은 언제나 원이다. 회전체는 축과 수직으로 자르면 항상 그 단면이 원이 되는 성질이 있다.

또 우리나라의 아름다운 도자기 역시 회전체의 대표적인 예다. 도자기를 만드는 과정을 생각하면 회전체라는 사실을 분명하게 알 수 있다.

도자기는 돌림판에 흙을 올려놓은 다음, 발판을 이용해 돌림판을 회전시키면서 손으로 그 모양을 빚는다. 돌림판이 돌면서 흙은 원운동을 하고, 손놀림에 따라 도자기의 두께를 조절하면 아름다운 곡선으로 된 도자기가 탄생한다. 도자기를 수학적으로 해석하면 회전축에서 어느 정도 떨어진 곡선이 회전축을 기준으로 회전해 생긴 입체도형인 셈이다.

이뿐만이 아니다. 여름철 바닷가에 갈 때 필요한 대표적인 물놀이 용품인 튜브는 구멍이 뚫린 도넛 또는 자동차 타이어를 닮았다. 튜브는 무엇을 어떻게 회전시켜 얻는 입체도형일까?

튜브는 직선을 회전축으로 해 일정한 거리만큼 떨어진 원을 회전시키면 된다. 수학에서는 튜브나 도넛과 같은 도형을‘원환면 또는 원환체(torus)’라고 부른다. 이 밖에도 우리 주변에는 무수히 많은 회전체가 있다. 주위를 관찰해 회전체를 찾고 수학적으로 해석해 보자. 자신도 모르게‘유레카’를 외치게 될 것이다.