d라이브러리

만일 사람의 손가락이 모두 12개였다면, 아마 우리는 10진법 대신 12진법을 사용했을 것입니다. 12진법을 사용했다면 세상은 얼마나 달라졌을까요? 5백 원 동전, 5천 원권 지폐 등이 없어지고 1백 원, 4백 원, 1천 원, 4천 원 등으로 화폐를 구성했을 가능성이 큽니다. 각종 숫자 키패드에서 *나 # 등의 키는 없어졌을 겁니다. 몇 시 혹은 몇 월을 두 자리 수로 나타낸다는 일을 상상할 수 없게 되었겠네요. 파이 데이는 3월 14일이 아니라 3월 18일이 되었을 겁니다. 그리고, 우린 아직 12세기를 살고 있었겠네요. 이런 상상 속에서 만들어진 주제를 만나볼까요? KAIST 사이버영재교육센터에서 2000년에 출제되었던 과제입니다.

12진법의 숫자로 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B를 사용하기로 하자. 12진법의 구구단(정확히는BB단) 표를 만들어보면 다음과 같다. 생각보다 규칙적인 꼴이 많음을 관찰할 수 있다. 12는 약수가 많기 때문이다. 10진법과 12진법의 구구단의 복잡도가 서로 비슷하다고 본다면, 12진법은 같은 개수의 자리로 좀 더 큰 수를 나타낼 수 있기 때문에 곱셈을 할 때 조금이나마 효율적이라고 볼 수 있다.
 

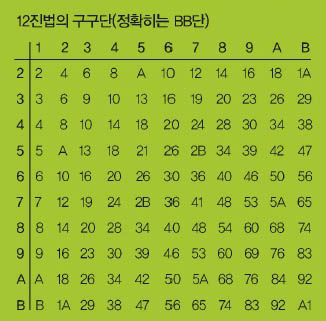
그렇다면 12진법에서의 배수 판정법은 어떨까? 역시 약수가 많아서 생각보다 어렵지 않을지 모른다.

문제 1

(1) 12진법에서는 10진법에서처럼 어떤 주어진 수가 2의 배수인지 아닌지 쉽게 판정할 수 있는 방법이 있다. 그것을 설명하여라. 3, 4, 6의 배수 판정법도 각각 설명하여라.

(2) 12진법에서의 B의 배수 판정법을 설명하여라.

문제 2

12진법에서 8의 배수와 9의 배수를 판정하는 방법을 각각 설명하여라. 만일 12진법에서 5의 배수를 판정하는 방법을 알고 있는 것으로 한다면, A의 배수는 어떻게 판정할 수 있을까?

이제 12진법에서 한 자릿수의 배수 판정법으로는 5의 배수와 7의 배수를 판정하는 것만 남았다. 이들은 앞에서 본 배수 판정법들을 응용할 수는 없고, 아예 다른 방법을 찾아봐야 할 것이다. 10진법에서도 유독 7의 배수 판정법이 잘 알려져 있지 않은데, 이런 경우의 배수 판정법들은 찾을 수 없는 것일까? 아니면 판정할 수 있는 다른 좋은 아이디어나 해결 방법이 있을까?

10진법에서의 7의 배수 판정법은 있다. 물론 2의 배수 판정법보다는 훨씬 복잡하지만, 3의 배수 판정법에 비교한다면 사실 난이도에 큰 차이가 없다. 여러 가지 아이디어와 방법들이 있으므로, 그것들을한 번 쭉 공부해보고, 그 후에 다시 12진법으로 돌아와서 그 5의 배수나 7의 배수 판정법을 탐구해보기로 하자.

문제 3

(1) 1001을 소인수분해하여라.

(2) 어떤 자연수가 11의 배수인지를 판정하려면, 각 자릿수를 차례로 더하고 빼고를 번갈아 반복하여 그 결과가 11의 배수인지를 살피면 된다. 예를 들어, 143과 814는 1-4+3=0, 8-1+4=11로 각각 11의 배수가 된다. 이 11의 배수 판정법을 참고하여 1001의 배수를 판정하는 방법을 찾고, 그 원리를 설명하여라.

(3) 위에서 찾은 1001의 배수 판정법이 7의 배수 판정법이나 13의 배수 판정법으로도 그대로 적용됨을 설명하여라.

문제 4

(1) 어떤 세 자리의 자연수 abc가 주어졌을 때, 100의 자리의 수 a에 두 배를 하여 나머지 두 자리 수 bc에 더한 수 bc+2a가 7의 배수이면, 원래의 수도 7의 배수라고 한다. 그 원리를 설명하여라.

(2) 어떤 자연수 n=10a+b가 주어졌을 때, 일의 자리의 수 b에 두 배를 하여 십의 자리 이상의 수 a에서 뺀 수 a-2b 가 7의 배수이면, 원래의 수도 7의 배수라고 한다. 그 원리를 설명하여라.

(3) 어떤 세 자리의 자연수 abc가 주어졌을 때, 각 자리의 수에 2, 3, 1을 곱하여 더한 수 2a+3b+c가7의 배수이면, 원래의 수도 7의 배수라고 한다. 그 원리를 설명하여라.

(4) 위의 세 사실과, 앞의 문제들에서 적절히 필요한 사실을 선택하여 7의 배수 판정법을 한 가지 정리하여 제시하여라.

위의 공부를 바탕으로, 이제 12진법에서 궁금했던 5의 배수와 7의 배수 판정법을 여러분 스스로의 힘으로 찾아보자.

문제 5

(1) 12진법에서 5의 배수 판정법을 두 가지 이상 찾고, 그 원리를 설명하여라.

(2) 12진법에서 7의 배수 판정법을 두 가지 이상 찾고, 그 원리를 설명하여라.

이번에는 두 자리의 수의 배수 판정법을 생각해보는 것은 또 어떨까?

문제 6

12진법에서 적당한 두 자리의 소수를 5개 택해서 그 각각의 배수 판정법을 찾고, 그 원리를 설명하여라. 그리고, 10진법이나 12진법 이외의 다른 진법도 한번 고려해 보면 어떨까?

문제 7

16진법에서 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F의 배수를 판정하는 방법을 각각 설명하여라.