d라이브러리

‘도시대항 국제수학토너먼트(TOT)’ 에서 만났던 수많은 멋진 문제들 중에서도 ‘대표적인 멋진 문제’ 를 꼽으라 한다면 필자에게 가장 먼저 떠오르는 문제가 하나 있습니다. 그것이 바로 이번 호에 소개할 문제입니다. 어떤 문제일지 궁금해지지 않나요? 여러분도 기억에 남는 멋진 문제를 하나쯤 갖고 있나요? 원래의 문제보다 조금만 쉽게 변형해서 소개하겠습니다.

TOT 1981년 고등부 5번 변형

격자 칸으로 구획된 한 사분면을 생각하자. 코너 칸에 평면 아메바 한 마리가 놓여 있다. 편의상 코너가 왼쪽 아래에 있다고 하자. 이 평면 아메바는 이분법으로 번식을 하는데, 한 마리가 둘로 분열되면서 각각 위 칸과 오른쪽 칸으로 한 마리씩 이동한다.
 

단, 한 칸에 아메바 두 마리가 들어갈 수는 없어서, 위 칸과 오른쪽 칸이 둘 다 비어 있을 때에만 분열할 수 있다. 이 아메바들은 한 번에 한 마리씩만 분열하는데 분열 시점이나 순서는 정해져 있지 않고, 죽어서 사라지거나 하지도 않는다. 코너 쪽의 3×3 영역을 아메바들의 집이라고 부르자. 모든 아메바가 집을 벗어날 수 있는가?

규칙에 따라 분열 순서를 적당히 택하며 관찰해 봅시다. 예를 들어 다음과 같습니다.
 

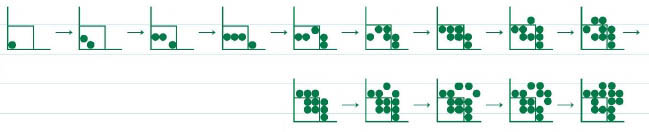
그럼, 집을 벗어나게 하는 것이 굉장히 갑갑하고 어려운 상황이라는 것을 느낄 수 있습니다. 여러분들 스스로 작업해 보면 더욱 그 느낌을 생생하게 가질 수 있을 것입니다. 즉, 이 문제의 답은 ‘벗어날 수 없다’ 일 거라는 추측이 듭니다. 그렇다면 그 추측을 어떻게 증명해야 할까요?

위와 같은 작업을 경험해보면, 우상으로 진행할수록 아메바가 늘어나는 품새로 볼 때, 좌하쪽의 칸이 우상쪽의 여러 칸의 모임과 대등할 만큼 가치가 큰 것이 아닐까 하는 생각을 할 수 있습니다. 좀 더 정밀하게 말하면, 아메바가 분열하기 전에 위치했던 한 칸이 아메바가 분열된 이후의 두 칸과 대등한 상황이라는 생각입니다. 혹은 조금 다르게 생각하면, 아메바가 분열하면서 크기가 절반씩인 두 마리로 분열된다고 생각해도 좋겠습니다. 그럼 각 칸의 위치에 따라 그 칸에 오게 되는 아메바의 크기가 결정되고, 아메바 전체의 크기의 합은 항상 일정함을 관찰할 수 있습니다. 이런 불변량에 착안하면 다음과 같은 풀이를 할 수 있습니다.


멋진 증명이지 않은가요? 원래의 문제는 3×3보다 더 줄여서, 코너쪽의 계단 꼴로 생긴 영역을 아메바들의 집으로 하는 것이었습니다. 이 경우에는 한 가지 관찰을 더 필요로 하는데, 과연 그 증명은 어떻게 이루어질까요? 이것은 독자 여러분의 몫으로 남깁니다.