d라이브러리

“박사님, 크, 큰일났어요! 뒤에 토네이도가….”
“허허. 빨리 뛰자꾸나. 그런데 토네이도에도 수학이 있다는 사실을 아느냐?”
“네? 수학이요? 글쎄….”
“연구실에 돌아가면 토네이도 실험을 하자꾸나.”
“네, 돌아갈 수 있으면요. 좀 더 빨리 뛰세요.”


자연의 신비한 곡선, 나선

자연현상이나 사물에서 쉽게 발견되는 나선은 오래도록 사람들의 관심의 대상이었다. 해바라기 씨앗의 배열, 절지동물인 노래기, 아이슬란드의 기후곡선, 포도나무의 덩굴, 염소의 뿔, 양배추의 단면 등에서 나선을 발견할 수 있다. 나선은 어쩌면 신이 자연 속에 감춰 놓은 신비하고 아름다운 곡선일지 모른다.

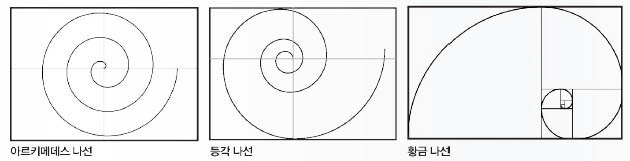
두꺼운 도화지로 세로 길이가 1cm, 가로 길이가 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13cm인 긴 띠를 만든 후 한 방향으로 접으면 일정한 간격으로 돌아가는 아르키메데스 나선을 만들 수 있다.
 

세로 길이가 1cm, 가로 길이가 1, 1, 2, 3, 5, 8, 13, 21cm인 긴 띠를 만든 후 한 방향으로 접으면 일정한 비율로 커지는 황금 나선을 만들 수 있다. 이웃하는 두 선분의 길이 비가 나선의 중심에서 멀어질수록 황금비, 즉 약 1:1.618에 가까워지기 때문에 붙여진 이름이다.
 

정점에서 뻗어 나간 모든 선과 일정한 각을 이루는 곡선을 등각 나선이라고 한다. 1638년 프랑스의 수학자이자 철학자인 데카르트가 처음 등각 나선이라고 불렀다.
 

아하! 생각이 쑥쑥! 수학으로 디자인하다

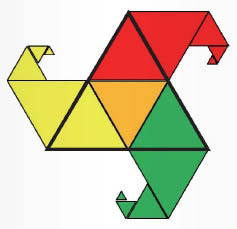
정삼각형은 각 변의 중점을 연결하면 작은 정삼각형으로 4등분된다. 그림과 같이 작은 정삼각형의 한 변에 같은 크기의 정삼각형을 거꾸로 그리고 다시 한 변의 길이가 $\frac{1}{2}$인 정삼각형을 그린다. 이 과정을 반복해 그린 뒤 세 가지의 색을 선택해 칠하면 바람개비 모양의 아름다운 나선이 생긴다. 이 모양은 2002년 한일월드컵 공인구인 피버노바의 불꽃 무늬를 닮았다

매는 먹이를 따라갈 때 등각 나선을 따라 비행하는 것으로 알려져 있다. 나선보다 직선으로 날면 훨씬 더 빠를 텐데, 매는 왜 나선으로 나는 걸까? 이유는 매의 눈이 양 옆에 있어서 머리를 기준으로 한쪽 방향에 있는 목표물을 볼수 있는 각도가 40˚이기 때문이다. 송골매는 등각 나선을 따라 날아야 최고 속도를 유지하면서 자신의 먹이를 따라갈 수 있다.
 

◎미션◎ 생활 속에서 다양한 나선을 찾아 재미있는 수학 이야기를 만들어 보세요.

예문 달팽이는 나선 모양의 집 속에 살아요. 저런! 실수로 그만 선인장 위에 떨어졌어요. “아야!” 얼마나 아플까요? 그런데 선인장이 반갑게 달팽이를 반깁니다. “반갑다! 난 네가 좋아. 너와 나는 닮은 점이 있거든!” “별꼴이야. 뭐가 닮았다는 거야?” 달팽이와 선인장에서 공통적으로 발견되는 것이 있다는 것을 수학동아 친구들은 알지요? 그래요. 바로 나선입니다.
딩동댕! ^.^