d라이브러리

땅따먹기 놀이에 대해 들어 본 적이 있나요? 출발점에서 손가락으로 돌을 튕겨 움직인 거리만큼 선을 그으면서 땅을 차지하는 놀이랍니다. 실제로 아메리카 대륙에 유럽인이 정착할 때, 말을 타고가 깃발을 먼저 꽂은 사람이 땅의 주인이 되었답니다. 하지만 고대 이집트에서는 땅을 나눌 때 정사각형 모양으로 나눴다고 해요. 수많은 다각형 중에 왜 정사각형일까요? 기다란 직사각형으로 나누면 어땠을까요? 지금부터 여러분께 땅을 나눠 주도록 하겠어요. 각자 원하는 모양의 땅을 만들어 그 위에 집을 지어 보기로 해요.

집짓기 1단계 : 내 땅 차지하기

선생님 : 사랑이, 기쁨이, 소망이에게 각각 4개의 나무말뚝과 20m짜리 노끈을 줄테니 원하는 모양의 네모난 땅을 만들어 보세요.
기쁨 : 저는 긴 땅을 갖고 싶어요. 한쪽에 집을 짓고 나머지는 정원으로 꾸밀래요.
소망 : 저는 네모반듯한 게 좋아요. 집도 연못도 네모반듯하게 만들 거예요.
사랑 : 네모난 연못? 네모난 물고기도 구해야겠네. 전 둘의 중간쯤 되는 네모로 할래요.
선생님 : 좋아요. 이제 자신의 땅에 말뚝을 박아 표시하세요.
기쁨 : 선생님~, 제 땅부터 봐 주세요. 전 가로 9m, 세로 1m짜리 기다란 땅을 만들었어요. 멋지지 않나요?
 

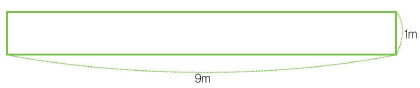
사랑 : 길어서 멋지긴 한데 집은 어디다 지을지 궁금하네. 제 땅이 딱 좋은 것 같아요. 집 짓기도 그렇고 정원 꾸미기도 그렇고. 전 가로 7m, 세로 3m짜리 땅이랍니다.
 

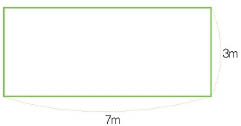
소망 : 전 네모반듯한 가로, 세로 5m짜리 정사각형 땅을 만들었어요.
 

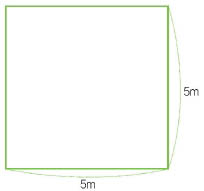
선생님 : 모두들 수고했어요. 그럼 이제 누가 가장 지혜로운 선택을 했는지 알아보기로 해요. 땅 1㎡당 100만 원에 팔 수 있다면 누가 가장 많은 돈을 벌 수 있을까요?
기쁨 : 아차! 그 생각을 못했네요. 일단 넓은 땅을 차지하고 봐야 하는 건데….
사랑 : 기쁨이의 땅 넓이는 9㎡, 제 땅은 21㎡, 소망이는 25㎡네요.
선생님 : 그래요. 소망이가 가장 경제적인 활동을 했군요.
기쁨 : 아~, 둘레가 정해져 있다면 정사각형일 때가 가장 넓이가 넓다는 걸 몰랐어요.
선생님 : 기쁨이도 너무 슬퍼하지 말아요. 기쁨이의 땅도 좋은 점이 있답니다. 같은 넓이일 때 가장 둘레가 길어지려면 어떤 모양이 좋은지 살펴보기로 해요.

집짓기 2단계 : 창이 큰 집 짓기

기쁨 : 그럼 제 땅을 기준으로 비교해 봐요. 제 땅은 넓이가 9㎡고 둘레는 (9×2)＋(1×2)로 20m예요.
 

만약 넓이가 9㎡인 정사각형을 만든다면 둘레가 (3×4)로 12m가 나와요.
 

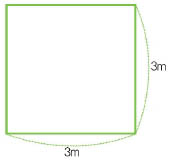
사랑 : 같은 넓이일 때, 둘레가 더 긴 쪽은 직사각형이군요.
기쁨 : 아하! 땅은 정사각형이 이익일지 몰라도 집은 직사각형으로 짓는 게 더 좋을 거란 생각이 들어요.
선생님 : 왜 그런 생각을 했지요?
기쁨 : 집의 둘레가 길면 창문도 많이 낼 수 있고 햇볕도 더 많이 들어오지 않을까요?
사랑 : 그래~, 집은 밝아야 좋지. 저도 집을 직사각형으로 짓고 싶어요.
소망 : 이제 집터도 정해졌고 벽도 세웠으니 지붕만 얹으면 되겠네요.

집짓기 3단계 : 튼튼한 지붕 올리기

선생님 : 지붕을 얹을 때는 어떤 점을 고려해야 할까요?
기쁨 : 우선 예뻐야죠.
사랑 : 예쁘기만 하면 될까? 비가 와서 빗물이 고인다면 지붕이 썩을 지도 모르잖아요.
선생님 : 좋은 지적이에요. 빗물이 잘 흘러 내려야 하고 눈이 쌓여도 잘 견딜 수 있어야겠지요.
소망 : 그럼 힘센 도형을 찾아야 할 텐데 변의 개수가 많을수록 힘이 세지 않을까요?
선생님 : 그럴듯한 생각이지만 다각형 중에서 가장 힘이 센 것은 삼각형이랍니다.
사랑 : 헉! 천하장사 도형이 삼각형이라고요? 뾰족해서 창처럼 콕콕 찌를 수 있으니그런 건가요? 변의 개수가 가장 적은 삼각형이 힘이 제일 세다니 이해가 잘 안 가요.
선생님 : 혹시 무거운 물건을 들어 올리는 크레인이 어떤 구조인지 기억하나요?
기쁨 : 튼튼한 강철로 만든 것 같은데 구조도 중요한 건가요?
선생님 : 어쩌면 재료보다 구조가 더 중요할 수도 있어요. 크레인에 쓰이는 트러스구조는 처음에 삼각형 모양으로 발명되었답니다. 여기 나무젓가락을 이용해 만든 삼각형과 사각형이 있어요. 각각의 이음매는 못으로 고정했답니다. 둘 중 어느 것이 더 튼튼할까요?
 

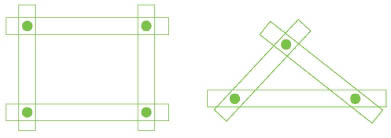
소망 : 그냥 보기에는 사각형이 더 튼튼해 보이는데요.
선생님 : 과연 그럴까요? 사각형의 한쪽 꼭짓점을 눌러 보면 어떻게 될까요?
사랑 : 한 쪽으로 찌그러질 것 같은데요.
선생님 : 맞아요. 그렇다면 삼각형은 어떨까요?
기쁨 : 그 모양 그대로 있을 것 같아요.
선생님 : 그렇죠. 이제 사각형과 삼각형 중 누가 힘이 센지 가려졌나요? 이러한 삼각형의 특성 때문에 트러스 구조가 탄생했고 지붕이나 다리와 같이 무거운 무게를 견뎌야 하는 구조물도 삼각형을 기본 도형으로 만든답니다.
소망 : 아하~, 정사각형 땅에 창이 큰 직사각형 집을 짓고 삼각형 지붕을 얹으면 기하학적으로 가장 훌륭한 집이 되는군요.
선생님 : 그래요. 이제 마지막으로 집안에 바닥을 깔아 보기로 해요.

집짓기 4단계 : 바닥 꾸미기

선생님 : 준비한 세 개의 타일 중 가장 마음에 드는 것을 골라 바닥을 깔아 보도록 해요.
 

기쁜 : 타일 중에 왜 오각형만 빠졌나요?
선생님 : 오각형은 바닥을 빈틈없이 메울 수 없기 때문이에요. 빈틈없이 메운다는 말은 한 꼭짓점에 모인 도형의 각의 합이 360°라는 뜻이에요. 오각형이 왜 안 되는지 같이 살펴보기로 해요.
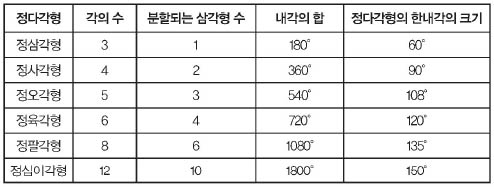
소망 : 먼저 오각형의 내각의 합을 아는 게 중요할 거 같아요. 도형의 내각의 합은 도형을 삼각형으로 나눠보면 알 수 있어요.
사랑 : 오각형은 세 개의 삼각형으로 나눌 수 있으니까 내각의 합은 180°×3=540°가 되겠네요.
소망 : 오각형의 한 내각의 크기는 내각의 합을 5로 나누면 되니까 540°÷5=108°가 되네요.
기쁨 : 아하! 오각형 세 개를 붙이면 108°×3=324°로 360°에서 36°가 남으니까 오각형으로 바닥을 빈틈없이 메울 수 없다는 거군요.
 

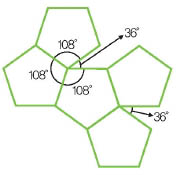
선생님 : 우와~, 별다른 설명을 하지 않아도 정말 멋진 추론을 해냈네요. 여러분이 알아 낸 것처럼 정삼각형, 정사각형, 정육각형 이 세 개의 정다각형만이 하나의 도형으로 바닥을 빈틈없이 메울 수 있답니다. 이렇게 바닥을 빈틈없이 메우는 것을 ‘테셀레이션’이라고 해요.
 

기쁨 : 그런데 다른 도형을 함께 써서 빈틈을 메울 순 없을까요?
 

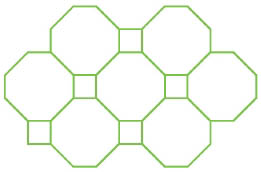
선생님 : 멋진 생각이에요. 정팔각형으로 시도해 볼까요?
소망 : 정팔각형은 한 내각의 크기가 135°니까 두 개를 이어붙이면 270°가 되고 360°가 되려면 90°가 모자라요. 남는 부분에 한 내각의 크기가 90°인 정사각형을 이어 붙이면 빈틈없이 메울 수 있어요.
 

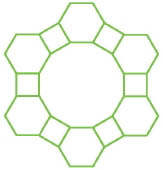
선생님 : 잘했어요. 이번에는 정십이각형으로 해 볼까요?
기쁨 : 정십이각형은 한 내각의 크기가 150°이므로 두 개를 이어 붙이면 300°가 돼요.
사랑 : 60°가 모자라니까 정삼각형을 이어 붙이면 되겠네요.
선생님 : 정말 잘했어요. 좀더 복잡한 걸로 생각해 봐요.
소망 : 앞의 표에서 내각의 크기의 합이 360°가 되는 도형들을 찾아 이어붙이면 될 거 같아요. 예를 들면 정사각형 90°와 정육각형 120°, 정십이각형 150°를 한 꼭짓점에 모이게 이어 붙이면 360°가 되지요.
선생님 : 우리 소망이 최고예요. 그림을 그려 확인해 볼까요?
 

선생님 : 이처럼 테셀레이션은 정말 다양한 방법으로 가능해요. 네덜란드의 판화가 에셔는 정육각형을 변형해 도마뱀을 그린 다음 테셀레이션한 작품을 만들기도 했지요.
선생님 : 아무튼 오늘 도형을 이용해 집 한 채를 짓느라 다들 수고했어요. 집 짓고 났더니 배고프지 않나요? 선생님이 맛있는 피자를 사 줄 테니 일정한 둘레에 가장 넓은 모양으로 잘라 먹는 내기 할까요?
일동 : 선생님 제발~, 그냥 공평하게 나누어 먹는 걸로 해요!