d라이브러리

Prologue_ 21세기 들어 양전자 두뇌를 갖추고 사람처럼 생각하는 로봇이 등장합니다. 이에 따라 로봇심리학이라는 학문이 새롭게 생겼지요. 로봇 제조 회사인 ‘US로보틱스’에서 로봇심리학자로 활동하며 평생에 걸쳐 로봇의 발달 과정을 지켜 본 수잔 캘빈 박사는 은퇴를 앞두고 한 인터뷰에서 지금까지 겪어 온 여러 가지 사건에 대해 이야기해 줍니다.

엉뚱한 창조주를 믿는 로봇

“네가 초점을…… 정확히 유지했어. 알고서 그런 거야?”

“초점? 그게 뭐죠?”

“에너지 빔을 수신 기지에 정확히 보냈다는 거야. 오차 범위 1만 분의 1초 안에서.”

“어떤 수신 기지요?”

“지구, 지구에 있는 수신 기지. 네가 초점을 정확하게 유지했어.”

파웰이 더듬거리며 대답하자 큐티가 화를 내며 홱 돌아섰다.

“두 사람에게 친절을 베푸는 건 정말 힘든 일이군요. 언제나 똑같은 환상만 지껄이니! 나는 주인님의 의지에 합당하게 모든 다이얼을 조정해서 평형 상태를 유지했을 뿐이에요.”

로봇 큐티는 사람이 자기를 만들어 냈다는 사실을 믿지 않습니다. 대신에 에너지 전송장치를 주인님이라고 믿고 따릅니다. 결국 큐티는 에너지 전송 장치를 주인님으로 믿는 종교를 만들고, 자기가 예언자가 되지요.

상황이 이렇게 되자 로봇 기술자인 파웰과 도노반은 에너지 전송 장치를 이용해 지구에 에너지 빔을 보내는 임무를 수행하지 못할까 봐 전전긍긍합니다. 하필이면 전자 폭풍이 다가오고 있기 때문에 에너지 빔의 초점을 수신기지에 맞추기가 더욱 어려워집니다. 초점을 못 맞추면 무슨 큰일이 나기에 그러는 걸까요?

초점이란 오목거울이나 볼록렌즈에 평행하게 들어온 빛이 반사되거나 굴절돼 한데 모이는 점을 말합니다.
 

수학에서 다루는 도형인 포물선에서도 초점을 찾아볼 수 있습니다. 포물선은 초점과 직선 한 개가 있을 때 초점과 직선으로부터의 거리가 똑같은 점을 이어 그린 곡선을 말합니다. 포물선은 오목거울과 마찬가지로 축에 평행하게 들어와 반사된 빛이 초점에 모입니다. 곧 오목거울의 단면이 포물선이라는 뜻이지요.

만약 초점이 수신 기지에 정확히 맞지 않으면 에너지 빔은 지구 표면에 떨어져 큰 피해를 입힐 것입니다. 이런 위기를 큐티는 어떻게 넘겼던 걸까요? 알고 보면 단순합니다. 큐티는 단지 주인님이라고 여겼던 에너지 전송 장치의 지시를 충실히 따랐을 뿐입니다. 진짜 창조주인 인간이 아닌 엉뚱한 기계에 복종했던 것이지만 결과가 좋으니 다행이었지요.

인공지능은 똑똑한 바보

수잔 캘빈이 브레인이 들어 있는 둥근 천장의 환상적인 공간에 들어섰을 때, 교대로 일하는 기술자 한 명이 브레인에게 이렇게 묻고 있었다.

“닭 한 마리 반이 하루 반 동안 달걀 하나 반을 낳는다면 닭 아홉 마리가 구 일 동안 달걀 몇 개를 낳게 되는 거지?”

브레인이 대답했다.

“54.”

컴퓨터는 우리가 수백, 수천 년이 걸려야 할 수 있는 계산을 순식간에 해 냅니다. 웬만한 계산은 우리가 미처 생각조차 하기도 전에 답이 나오지요. 인공지능 컴퓨터인 브레인의 능력을 시험하기 위해 기술자가 문제를 던졌습니다. 우리도 함께 계산해 볼까요?

먼저 닭 한 마리가 하루에 달걀을 몇 개 낳는지 알아야 합니다. 닭 한 마리 반이 하루 반에 달걀 하나 반을 낳는다고했으니까 차근차근히 계산해 봅시다. 혼동을 막기 위해 닭 한마리 반을 A로 표시합시다.

A가 1.5일에 낳는 달걀=1.5개
1.5일에 달걀 1.5개를 낳으므로, 1일에는 달걀 1개를 낳습니다.
A가 1일에 낳는 달걀=1개
이제 A를 다시 닭 한마리 반, 즉 1.5마리로 바꿔 봅시다.
닭 1.5마리가 1일에 낳는 달걀=1개

따라서 닭 1마리가 1일에 낳는 달걀은 $\frac{2}{3}$개가 됩니다. 문제는 닭 9마리가 9일 동안 낳는 달걀의 수를 묻고 있으므로, 9×9×$\frac{2}{3}$=54, 정답은 54개가 됩니다.

인공지능 컴퓨터인 브레인은 문제를 듣자마자 정답을 내놓았습니다. 하지만 과연 브레인이 똑똑하다고 말할 수 있을까요? 상식적인 사람이라면 문제를 듣자마자 “닭 한 마리반이 어디 있어? 달걀 한 개 반은?”라고 의아해할 것입니다.

기술자가 브레인을 시험하기 위해 낸 문제는 컴퓨터의 한계를 보여 주고 있는 대목입니다. 계산은 사람보다 훨씬 빠를지 몰라도 사람이라면 기본적으로 갖추고 있는 상식이 부족한 헛똑똑이라는 소리지요. 물론 언젠가 인공지능이 완벽해져서 사람과 똑같은 반응을 하는 컴퓨터가 등장할지도 모릅니다. 과연 그 날은 언제일까요?

각도로 만든 거리 단위
 

하지만 우주선 맨 앞에 있는 마지막 방은 조금 달랐다. 무반사 유리로 만든 곡선 유리창은 금속 일색인 내부에서 처음 보는 변화였다. 그 밑에 큰 계기판 하나가 붙어 있는데, 하나밖에 없는 바늘은 0에 고정돼 있었다.

“저것 좀 보세요!”

도노반이 정교한 저울에 씌어 있는 단어를 가리키며 말했다. 천체 간의 거리를 3.26광년 단위로 나타내는‘ 파섹’이라는 단어였다. 그리고 곡선으로 매긴 눈금 오른쪽 끝에는‘ 1,000,000’이라는 숫자가 작게 적혀 있었다.

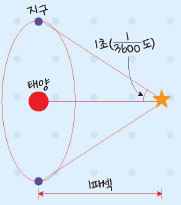
기술자들은 앞서 등장한 브레인에게 우주선을 만들어 시험하는 일을 맡깁니다. 브레인은 우주선을 만들어 내고 파웰과 도노반은 우주선을 시험할 기술자로 뽑힙니다. 그런데 이 때 두 사람이 발견한 계기판이 좀 특이합니다. 우주선 조종실인데 계기판이 달랑 하나뿐입니다. 거기에 쓰여 있는 단위는 파섹이고요. 파섹은 3.26광년, 즉 빛이 3.26년 동안움직이는 거리를 의미하지요. 3도 아니고 4도 아닌 3.26이라니, 왜 하필 이런 애매한 숫자로 단위를 만들었는지 궁금해지네요. 1파섹을 어떻게 정했는지 오른쪽 그림을 봅시다.

지구는 태양의 주위를 돌고 있습니다. 어떤 한 순간에 멀리 떨어져 있는 별을 관측한 뒤 6개월이 지나면 지구는 태양의 반대편에 와 있습니다. 이 때 똑같은 별을 관측하면 위 그림처럼 두 직선 사이의 각도를 잴 수 있습니다. 이 각도의 절반이 1초, 즉 3600분의 1도가 되는 거리를 1파섹이라고 합니다. 1파섹을 광년으로 환산하면 3.26광년이 되는 것이지요.

멀리 떨어진 천체까지의 거리를 직접 재는 것은 불가능합니다. 그래서 천문학자들은 이처럼 지구의 공전으로 생기는 각도를 이용해 거리를 계산합니다. 이 과정에서 생긴 단위가 바로 파섹이고요. 평소에는 잘 쓰지 않아 생소한 단위지만 알고 보면 천체의 거리를 계산하는 방법이 담겨 있는 재미있는 단위랍니다.

어느 장단에 맞춰 춤을 출까?

“가령 어떤 로봇이 위험한 곳으로 다가가다가 그곳이 위험하단 사실을 깨달았다고 쳐. 그럼 제3원칙이 이 로봇을 돌아서게 만드는 거야. 이번엔 인간이 그런 위험 속으로 들어가라고 명령했다고 해보자. 그러면 제2원칙이 다른 것보다 강하게 올라가기 때문에 모든 위험을 무릅쓰고 명령을 따르겠지.”

“으흠. 그건 저도 알아요. 그런데 그게 어떻다는 거예요?”

“스피디는 최신 모델이야. 전문 능력이 탁월하고, 제작비가 전함 한 척을 만드는 비용만큼이나 비싸. 쉽게 파괴돼선 안 되는 물건이지.”

“그래서요?”

“그래서 제3원칙이 강하게 주입된 거야.”

이번에는 수성 기지에서 일하는 로봇 스피디에 관한 이야기입니다. 파웰과 도노반은 스피디에게 연료로 쓸 셀레늄을 구하라는 명령을 내립니다. 그런데 스피디는 돌아올 생각을 하지 않고 셀레늄 웅덩이 주위를 빙글빙글 돌기만 합니다. 왜 그럴까요?

제2원칙에 따르면 로봇은 인간의 명령에 복종해야 합니다. 제3원칙에 따르면 로봇은 스스로를 보호해야 합니다. 보통제2원칙이 제3원칙보다 강하기 때문에 로봇은 명령에 따르는 일을 더 중요하게 여깁니다. 하지만 스피디는 최신 모델이라 제3원칙이 강하게 주입돼 있다고 하네요. 여기서 문제가 생깁니다.

스피디는 제2원칙에 따라 셀레늄 웅덩이로 향합니다. 그런데 가까이 갔더니 그 곳이 위험하다는 사실을 알게 됩니다.그러자 제3원칙에 따라 스피디는 웅덩이에서 멀어지려 합니다. 웅덩이에서 멀어지면 다시 제2원칙에 따라 가까이 다가가고, 다가가면 제3원칙에 따라 멀어지는 일이 반복됩니다. 결국 주위를 빙글빙글 돌기만 하는 것이죠. 이런 상황을 수학에서는 역설이라고 합니다.

파웰과 도노반은 최후의 수단으로 제1원칙을 이용하기로 합니다. 파웰이 뜨거운 태양이 내리쬐는 그늘 밖으로 걸어가자 마침내 스피디가 정신을 차리고 구조하러 옵니다. 모든 원칙 중에서 가장 중요한 제1원칙을 이용해 스피디를 되찾은 것이죠.

역설에 빠진 로봇

“래닝 박사님, 바보 같은 말씀 하지 마세요. 안에 사람이 있는 저택에 총을 쏘려고 하는 미친놈이 있으면 로봇은 어떻게 해야 하죠? 아마 그 미친놈을 당장 꼼짝 못하게 묶어야 할 거예요. 그렇지 않나요?“

“물론 그럴 거요.”

“그런데 꼼짝 못하게 하기 위해서 그 미친놈을 죽여야 한다면…….”

래닝의 목에서 희미한 신음이 흘러나왔다. 그게 전부였다.

“그건 이래요, 래닝 박사님. 물론 로봇은 그 미친놈을 죽이지 않으려고 최선을 다하겠지요. 미친놈이 죽게 되면 그 로봇은 갈등이 일어날 때마다 머리가 돌지 모르기 때문에 정신 치료도 받아야 하고요. 제1원칙을 지키기 위해서 제1원칙을 어겼으니까요.”

어떤 원칙을 이용하면 알 수 있을지 생각해 봅시다. 제1원칙에 따르면 로봇은 사람에게 해를 입힐 수 없으며 인간을 보호해야 합니다. 만약 사람에게 해를 입힐 수 있다면 그건 로봇이 아니라는 증거가 되지요.어떤 정치가가 있는데, 그가 사람이 아닌 로봇이라는 소문이 퍼집니다. 몸을 검사해 볼 수 없는 상황에서 사람인지 로봇인지를 알려면 로봇공학의 3원칙을 이용해야 합니다.

하지만 누군가가 주인에게 해를 입히려는 상황에 처한다면 로봇은 어떻게 해야 할까요? 당연히 주인을 지켜야 하지만, 그러려면 주인을 해치려는 악당에게 해를 입히는 셈이 됩니다. 인간을 보호하기 위해 인간에게 해를 입혀야 하는, 즉 제1원칙을 지키기 위해 제1원칙을 어겨야 하는 상황이 되는 것이죠. 로봇심리학자인 캘빈 박사는 이런 상황에 처한 로봇은 갈등으로 인해 미쳐 버린다고 이야기합니다.

맞습니다. 이번에도 역설에 대한 이야기입니다. “스스로 머리를 깎지 않는 모든 사람의 머리를 깎아 주는 이발사”나 “모든 크레타 인은 거짓말쟁이라고 말하는 크레타 인” 등이 잘 알려진 역설입니다. 이발사는 자기 머리를 깎을 수도 깎지 않을 수도 없는 상황에 처하고, 크레타 인의 말은 거짓인지 아닌지 아리송합니다.

이 정치가의 정체가 사람인지 로봇인지 이야기를 더 살펴봅시다. 어느 날 한 연설장에서 누군가가 정치가에게 시비를 겁니다. 로봇이 아니라면 자기를 한 대 때려 보라는 것이지요. 망설이던 정치가는 그 사람에게 주먹을 한 대 날립니다. 그 이후 로봇이라는 소문은 사라지고 정치가는 당선이 됩니다.

하지만 엄밀히 따지면 아직도 알 수는 없습니다. 왜냐하면 그 정치가가 때린 게 사람이 아니라 로봇이라면 이야기는 또 달라지거든요.