d라이브러리

3월 14일은 남자가 여자에게 사랑을 고백하는 ‘화이트데이’로 잘 알려져 있다. 하지만 수학계에서는 원주율(π, 파이)인 3.14를 기념하며 소수점 아래 펼쳐진 원주율을 외우는 파이데이로 지키고 있다. 끝을 알 수 없는 π의 신비를 밝히기 위해 동서양의 수많은 수학자들은 시간과 노력을 아끼지 않았다. 그들의 발자취를 따라 π의 정체를 알아보자.


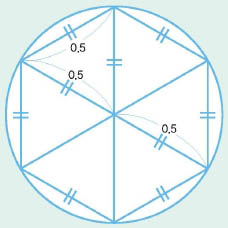
사람들은 수를 표시하고 편리하게 계산하기 위해 0이나 음수같이 다양한 수를 만들어 냈다. 하지만 π는 원이나 타원같은 도형 속에 오래 전부터 숨어 있던 자연의 수다. 원주율을 표시하는 π는 원 둘레의 길이를 지름의 길이로 나눈 값이다. π값은 예로부터 3보다 크다고 알려져 있었다. 원과 그 안에 꼭 들어가는 정육각형을 그려 보자. 원의 지름이 1이라면 정육각형 한 변의 길이는 0.5다. 정육각형은 6개의 정삼각형으로 쪼갤 수 있으므로 정육각형 둘레의 길이는 변 6개의 길이, 즉 3이다. 그림에서 보듯이 원 둘레의 길이는 정육각형 둘레의 길이보다 길다. 그러므로 π값은 3보다 크다.
 

π의 세계 신기록

지난 8월, 일본 치쿠바대학교 연구팀은 슈퍼컴퓨터를 이용해 π값을 소수점 2조 5769억 8037만 자리까지 계산했다고 밝혔다. 계산에 걸린 시간은 총 73시간 36분이었다. π값을 가장 많이 외우는 기록은 63세의 일본인 아키라 하라구치가 세웠다. 그는 2006년 16시간 30분에 걸쳐 π값을 소수점10만 번째 자리까지 외우는 데 성공했다.
 

 
중국에서 원주율의 역사는 기원전 1000년경으로 거슬러 올라간다. 중국에서 가장 오래된 수학책 ‘주비산경’에는 “지름이 1일 때, 원의 둘레는 3”이라 하여 π값을 3으로 간주했다. 263년 위나라의 유휘는 고대 중국 수학을 총정리한 ‘구장산술’을 통해 자신이 밝혀 낸 π값을 공개했다. 그는 아르키메데스와 같은 방법으로 정192각형이 원에 접해 있는 경우를 계산해 3.141024〈 π〈3.142704라는 것을 구했다. 그 뒤 정3072각형을 이용해 π값이 약 3.1416이라는 것도 밝혔다. 5세기경 송나라의 조충지는 π값을 소수점 여섯째 자리인 3.1415926〈 π〈3.1415927 까지 계산했다. 그가 사용한 방법은 정확하게 알려지지 않았지만 아르키메데스나 유휘의 방법과 같다면 정12288각형까지 계산한 것으로 보인다. 이 값은 그 뒤 1000년 가까이 세계에서 가장 정확한 π값으로 남아 있었다.

1596년 독일의 수학자 루돌프 반 쿨렌은 아르키메데스와 같은 방법으로 π값을 계산하는 데 평생을 바쳤다. 무려 320억각형의 둘레 길이를 계산해 소수점 35자리까지 구한 π값을 발표했다. 마지막 숫자 288은 그의 묘비에도 새겨졌다. 이처럼 다각형을 이용해 π값을 얻는 방법은 엄청난 시간과 노력이 필요했다.


끝없이 이어지는 π의 신비

수학자들은 π값을 구하는 새로운 방법을 찾기 시작했다. 첫 주자로 영국의 수학자 존 윌리스는 1655년 펴낸 책 ‘무한산술’에서 π값을 무한곱으로 표현하는 공식을 발표했다.
 

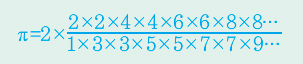
이어 수학에 미적분학이 발달하면서 π값을 계속된 항의 합으로 나타내는 식이 등장했다. 1682년 독일의 수학자 라이프니츠는 스코틀랜드 수학자 그레고리가 1671년 발견한 무한식을 이용해 π값을 구하는 공식을 내놓았다.
 

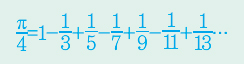
윌리스와 라이프니츠의 공식과 같이 π값을 효율적으로 계산하는 방법이 등장하면서 점점 더 정확한 결과가 나왔다. 영국의 천문학자 존 마친은 1706년 π값을 소수점 100자리까지 계산했다. 1844년에는 독일의 수학자 요한 다제가 소수점 200자리까지 구했다. 1873년 영국의 수학자 윌리엄 생크스는 15년에 걸쳐 π값을 소수점 707자리까지 계산했다. 안타깝게도 1945년 생크스의 계산에서 527자리부터 오류가 있는 것으로 밝혀졌다. 다각형을 이용한 아르키메데스의 방법으로 소수점 35자리까지 계산할 수 있었다면, 무한히 더하는 방법으로는 500자리를 조금 넘는 정도가 한계라는 것이다. 사람을 대신해 컴퓨터가 계산에 활용되면서 π값은 놀랄만큼 정확해졌다. 1949년 미국 연구팀은 세계 최초의 전자식 계산기인 '에니악'을 이용해 70시간 만에 소수점 2037자리 까지 계산했다. 1973년 프랑스에서는 하루 만에 100만 번째 자리까지 계산해 내기도 했다. 하지만 컴퓨터 성능이 아무리 좋아진다 해도 끊임없이 계속되는 수 π의 신비는 영원할 것이다.