
서울 전역에 전기를 공급할 새로운 발전소가 세워졌다고 가정해 봐요. 이때 전기선을 연결하는 변전소와 전봇대를 어디에 설치하는 게 좋을까요? 가장 싼 가격으로 가장 많은 지역에 전기를 보낼 수 있도록 연결하는 게 좋겠죠? 즉, 가장 적은 비용이 드는 경로를 찾아야 해요. 바로 이때 ‘최소 비용 신장 트리 알고리즘’이 쓰여요.
먼저 신장 트리가 뭔지 알아볼까요? 신장 트리는 각 지점을 점으로 표시하고, 그 사이를 선(신장)으로 연결한 간략한 그래프(트리)를 말해요. 이때 중요한 점은, 출발점으로 돌아가는 경로인 ‘사이클’이 없어야 한다는 거예요. 트리의 정의가 바로 ‘사이클이 없는 그래프’거든요. 사이클이 있으면 비용을 계산할 때 필요하지 않은 금액을 계속 더할 위험이 있답니다.
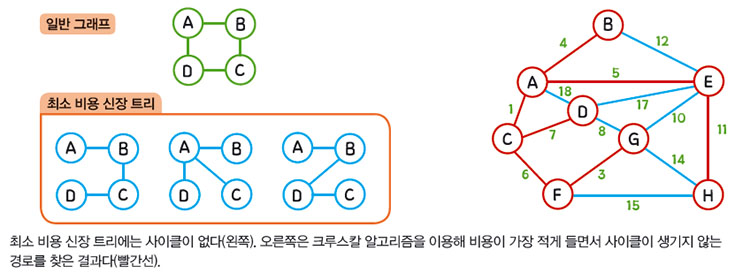
예를 들어 A, B, C, D 네 지점을 잇는 그래프를 살펴볼게요(오른쪽 페이지(아래 그래프)). 일반적인 그래프를 그릴 때는 A-B-C-D 순으로 길을 이은 다음, D에서 나온 선이 앞의 세 점 중 어느 곳으로도 연결될 수 있어요. 하지만 신장 트리에서는 A-B-C-D에서 끝이 나야 한답니다. D에서 나온 선이 앞의 세 점 중 어느 곳과도 연결되어서는 안 되지요.
최소 비용 신장 트리 알고리즘은 신장 트리를 어떤 순서로 그렸을 때 가장 비용이 적게 들지를 찾는 과정이에요. 가장 먼저, 지도를 점과 선으로 간략하게 만드는 것부터 시작해요. 각 지점을 점, 지점들을 잇는 ‘길’을 선으로 표시하는 거지요. 그리고 각 선마다 가중치를 두는데, 이 가중치는 그 선을 만드는 데 들어가는 ‘비용’을 의미해요. 한 지점에서 다른 지점으로 건너갈 때마다 가중치를 더해서 비용을 계산해요. 가장 적은 비용이 드는 경로가 답이 되는 거지요.
재미있게도 최단 거리가 반드시 최소 비용 경로는 아니에요. 예를 들어 섬과 섬을 이을 때 큰 돈을 들여 거대한 현수교를 하나 지으면 최단 거리가 돼요. 반면 섬에서 육지로 한 번 갔다가 다시 다른 섬으로 가도록 짧은 현수교 두 개를 짓는다면, 건설 비용이 절반만 든다고 가정해 봐요. 이 경우 최소 비용을 위해서는 다리 두 개를 짓는 게 더 좋은 방법이랍니다.
최소 비용이 드는 경로를 찾는 방법은 크게 두 가지가 있어요. ‘크루스칼 알고리즘’과 ‘프림 알고리즘’이지요. 크루스칼 알고리즘은 비용이 적게 드는 순으로 경로를 하나씩 그려가는 방법이에요. 가장 가중치가 작은 선을 골라 표시하고, 그 다음 작은 선을 다시 표시하는 과정을 계속 반복하는 거예요. 단, 사이클이 만들어지는 경로는 아무리 비용이 적더라도 사용하지 않아요. 크루스칼 알고리즘은 경로를 차례대로 하나씩 찾기 때문에 다루기 쉬워요. 하지만 점의 수가 늘어날수록 시간이 오래 걸릴 수 있지요.
먼저 신장 트리가 뭔지 알아볼까요? 신장 트리는 각 지점을 점으로 표시하고, 그 사이를 선(신장)으로 연결한 간략한 그래프(트리)를 말해요. 이때 중요한 점은, 출발점으로 돌아가는 경로인 ‘사이클’이 없어야 한다는 거예요. 트리의 정의가 바로 ‘사이클이 없는 그래프’거든요. 사이클이 있으면 비용을 계산할 때 필요하지 않은 금액을 계속 더할 위험이 있답니다.
예를 들어 A, B, C, D 네 지점을 잇는 그래프를 살펴볼게요(오른쪽 페이지(아래 그래프)). 일반적인 그래프를 그릴 때는 A-B-C-D 순으로 길을 이은 다음, D에서 나온 선이 앞의 세 점 중 어느 곳으로도 연결될 수 있어요. 하지만 신장 트리에서는 A-B-C-D에서 끝이 나야 한답니다. D에서 나온 선이 앞의 세 점 중 어느 곳과도 연결되어서는 안 되지요.

최소 비용 신장 트리 알고리즘은 신장 트리를 어떤 순서로 그렸을 때 가장 비용이 적게 들지를 찾는 과정이에요. 가장 먼저, 지도를 점과 선으로 간략하게 만드는 것부터 시작해요. 각 지점을 점, 지점들을 잇는 ‘길’을 선으로 표시하는 거지요. 그리고 각 선마다 가중치를 두는데, 이 가중치는 그 선을 만드는 데 들어가는 ‘비용’을 의미해요. 한 지점에서 다른 지점으로 건너갈 때마다 가중치를 더해서 비용을 계산해요. 가장 적은 비용이 드는 경로가 답이 되는 거지요.
재미있게도 최단 거리가 반드시 최소 비용 경로는 아니에요. 예를 들어 섬과 섬을 이을 때 큰 돈을 들여 거대한 현수교를 하나 지으면 최단 거리가 돼요. 반면 섬에서 육지로 한 번 갔다가 다시 다른 섬으로 가도록 짧은 현수교 두 개를 짓는다면, 건설 비용이 절반만 든다고 가정해 봐요. 이 경우 최소 비용을 위해서는 다리 두 개를 짓는 게 더 좋은 방법이랍니다.
최소 비용이 드는 경로를 찾는 방법은 크게 두 가지가 있어요. ‘크루스칼 알고리즘’과 ‘프림 알고리즘’이지요. 크루스칼 알고리즘은 비용이 적게 드는 순으로 경로를 하나씩 그려가는 방법이에요. 가장 가중치가 작은 선을 골라 표시하고, 그 다음 작은 선을 다시 표시하는 과정을 계속 반복하는 거예요. 단, 사이클이 만들어지는 경로는 아무리 비용이 적더라도 사용하지 않아요. 크루스칼 알고리즘은 경로를 차례대로 하나씩 찾기 때문에 다루기 쉬워요. 하지만 점의 수가 늘어날수록 시간이 오래 걸릴 수 있지요.

프림 알고리즘은 아무 점이나 선택해 연결된 점가운데 가장 비용이 적은 곳으로 이어가는 방식이에요. 연결되는 점이 늘어날수록 선택할 수 있는 경로의 수도 늘어나지요. 크루스칼 알고리즘과 달리, 여러 점에 연결된 선들을 한꺼번에 탐색하기 때문에 점의 수가 많을 때 크루스칼 알고리즘보다 빠른 속도를 낼 수 있답니다.












