d라이브러리

2008년 개봉한 일본 영화 ‘용의자 X의 헌신’은, 인간 심리를 섬세하고 생생하게 표현해 내는 추리소설 작가 히가시노 게이고의 소설을 원작으로 한다. 사건이 미궁에 빠지자, 담당 형사 우츠미는 ‘괴짜 갈릴레오’라는 별명을 가진 천재 물리학자 유카와 교수에게 도움을 청한다. 그는 사건을 추리하던 중, 야스코 옆집 사람이 이시가미 선생이라는 것을 알게 된다. 이로써 사건은 새로운 국면으로 접어든다. 이시가미 선생은 완벽한 수학 증명이야말로 세상에서 가장 아름다운 것이라고 믿는 고등학교 수학교사로, 대학 시절 이름을 날린 수학 천재였다.


역사상 가장 많은 사람이 도전한 난제

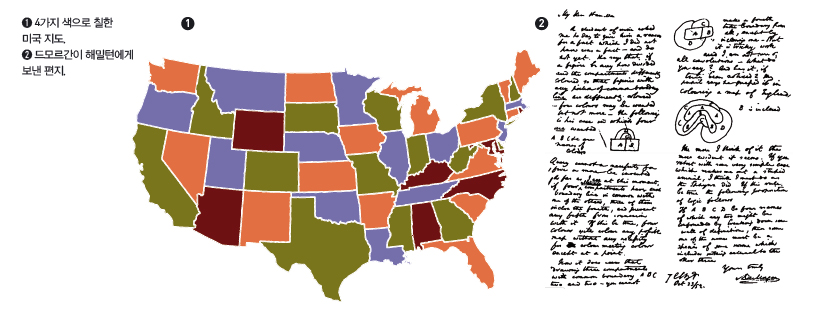
유카와 교수는 우츠미 형사와 식사를 하다가 대학 시절 기억을 떠올린다. 물리학도였던 그는, 당시 교정 벤치에 앉아 ‘4색 문제(four color problem)’ 증명에 몰두하고 있는 수학과 학생 이시가미를 발견했다. 이시가미는 컴퓨터를 이용한 4색 정리 증명이 아름답지 못하다고 생각해 인간의 두뇌를 이용한 아름다운 증명 방법을 찾고 있었다.

과연 수학 천재를 몰두케 했던 4색 문제란 무엇일까. 1852년 대학원생이던 영국의 프랜시스 구드리는 영국 지도를 색칠하다가 ‘지도 상에서 서로 인접한 영역을 서로 다른 색으로 칠하려면 최소한 몇 가지 색이 필요할까’라는 의문이 떠올랐다. 그는 영국 지도는 4가지 색만으로 가능하다는 것을 알게 됐지만, 지도 모양이 아주 복잡할 때도 4색으로 칠할 수 있을지는 확신이 없었다. 결국 그는 남동생 프레드릭 구드리의 스승이었던 수학자 오거스터스 드모르간(1806~1871년)에게 문의했는데, 그 역시 증명하지 못했다. 드모르간은 고민 끝에 수학자 윌리엄 해밀턴(1805~1865년)에게 도움을 청하는 편지를 보냈다. 이렇게 4색 문제가 점차 세상에 알려졌다.

이 문제는 각을 3등분하는 ‘작도 불가능 문제’와 더불어 역사상 가장 많은 사람들이 도전한 문제다. 문제 자체가 쉽게 이해되기 때문에 만만하게 여겨지는 데다, 누구나 어렸을 때 지도를 색칠해 본 경험이 있어서인지 수학을 제대로 공부하지 않은 아마추어도 증명을 시도하는 경우가 많다. 19세기 최고 수학자 헤르만 민코프스키(1864~1909년)도 4색 문제를 만만하게 보고 금방 풀 수 있다고 호언장담했지만, 결국 성공하지 못했다.



그는 이후 “하늘이 나의 오만함에 화가 난 것 같다. 내 증명에는 오류가 있다”며 실패를 인정했다. 1879년에는 수학자 알프레드 켐프(1849~1922년)가, 1880년에는 피터 테이트(1831~1901년)가 각각 증명을 내놓았다. 한 동안 합당한 것으로 여겨졌는데, 둘 다 11년 천하로 끝나고 말았다. 켐프의 증명은 1890년에, 테이트의 증명은 1891년에 잘못됐다는 게 밝혀졌기 때문이다.



그러나 실패라고 볼 수는 없었다. 켐프의 증명에 오류가 있다는 것을 밝힌 퍼시 히우드(1861~1955년)는 검증 과정에서 새로운 진보를 이뤄냈다. 켐프의 방법을 활용해 아무리 복잡한 지도라도 5가지 색이면 충분하다는 성질을 증명한 것이다. 뿐만 아니라 이 방법은 평면 지도를 넘어 곡면 지도에도 적용할 수 있었다. 결과적으로 보면 켐프와 히우드는 ‘실패는 성공의 어머니’라는, 다소 진부한 격언을 진부하지 않게 만든 사례인 셈이다. 이처럼 4색 문제가 제기되고 38년 만에 5색 정리까지는 증명이 됐지만, 여기서 한 가지 색을 줄이는 과정은 순탄치 않았다.

“컴퓨터 증명은 수학 본질에 맞지 않다”

이렇게 지난한 과정을 거친 뒤, 결국 4색 문제는 컴퓨터가 증명했다. 이제는 ‘4색 정리(four color theorem)’로 불린다. 1976년 미국 일리노이대 케네스 아펠(1932~2013년)과 볼프강 하켄(1928~ )은 새로운 방법으로 4색 문제에 접근했다. 지도 모양에 따라 나타나는 수많은 경우를 1936가지 유형으로 분류한 것이다(이후 연구에서는 유형 수를 더 줄일 수 있었다). 그 뒤, 각 유형을 일일이 컴퓨터로 분석했다. 무려 1200시간 동안 쉬지 않고 컴퓨터를 돌린 결과, 인접한 영역을 각각 다른 색으로 칠하는 데 필요한 최소 색상은 4가지라는 것을 증명할 수 있었다. 사실 컴퓨터를 이용해 증명하겠다는 아이디어는 독일 수학자 하인리히 헤슈(1906~1995년)가 처음 생각해냈다. 그는 독일보다 성능 좋은 컴퓨터를 갖춘 미국에 가서 하켄과 만났다. 다시 말해 컴퓨터를 이용해 증명한 주인공은 아펠과 하켄이지만, 그 토대를 구축한 사람은 헤슈다. 이후에도 그는 증명을 간결하게 만드는 연구를 진행했다.하지만 컴퓨터 증명을 인정해야 하는지에 대해선 아직도 논란이 분분하다. 결국 증명은 됐지만, 4색 정리는 컴퓨터만 해결할 수 있는 유일한 수학 문제로 남았기 때문이다. 이게 논란이 되는 이유는, 수학이 과학과 본질적으로 다르기 때문이다. ‘모든 현상에는 이유와 원인이 있다’고 믿는 물리학자 유카와는 ‘과학은 기본적으로 관찰하고 가설을 세운 후 실험으로 실증하는 것’이라고 정의한다. 실제로 과학에서 가설은 실증을 통해 비로소 진리가 될 수 있다. 수학은 다르다. 사유를 기본으로 하기 때문에 머릿속에서 시뮬레이션하는 ‘사고실험’이 중요하다고 본다. 물리 현상을 탐구하는 게 물리학이고 화학 현상을 탐구하는 게 화학인데, 수학은 현상 자체가 존재하지 않기 때문에 머리로 사유하고 머리로 검증하는 게 중요하다는 말이다. 이런 측면에서 볼 때 인간의 머리가 아니라 컴퓨터가 증명한 4색 정리는, 수학의 본질에 부합하지 않는다. 그래서 이시가미가 오랜 시간 동안 4색 문제 증명에 대해 불만족스러워했던 것이다. 4색 문제는 인간의 두뇌를 통한, 보다 우아하고 단순한 증명을 기다리고 있다.




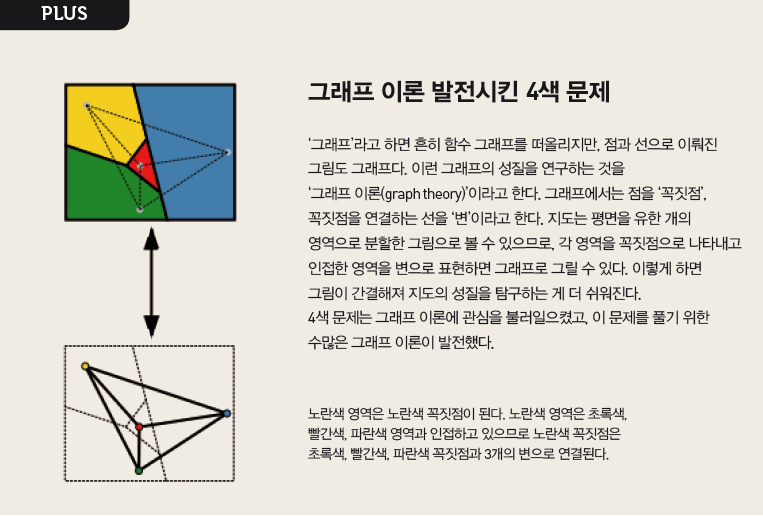
다시 영화로 돌아가보자. 유카와 교수와 이시가미 선생은 대학 졸업 17년 만에 이번 사건으로 재회한다. 유카와 교수는 수학 연구를 정상이 단 하나인 산을 오르는 것에 비유하면서 “수학에서는 정상에 오르는 여러 경로 중 가장 단순하고 합리적인 길을 알아내는 것이 중요하다”고 말한다. 이에 이시가미 선생이 “수학에는 세기의 난제 같이 오를 수 없는 산이 있다”고 응대하자 유카와 교수는 세기의 난제 중 하나인 리만 가설을 부정하는 증명을 이시가미 선생에게 건넨다. 그는 술잔을 기울이는 유카와 교수를 옆에 둔 채 밤을 새 그 증명의 근본적인 문제를 밝힌다. 유카와 교수는 이시가미의 천재성이 건재하다는 걸 알아챈다. 이시가미가 근무하는 고등학교를 찾은 형사들은 “학생들이 선생이 출제한 수학 문제를 어려워한다”고 말한다. 그러자 이시가미는 “내가 낸 문제는 예를 들어, 기하 문제처럼 보이지만 사실 함수 문제이기 때문에 관점만 바꾸면 어렵지 않게 풀 수 있다”고 답변한다. 이는 살인사건을 푸는 결정적인 힌트가 된다. 평소 야스코를 흠모하던 이시가미가 천재적 두뇌를 이용해 사건을 조작했던 것이다. 마치 기하 문제를 함수 문제로 바꿨듯이.