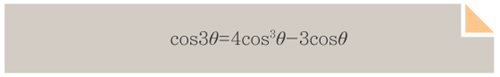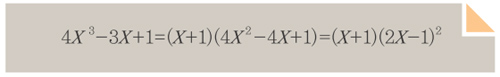자와 컴퍼스만 가지고 임의의 각을 삼등분할 수 있을까.
사실 이 문제는 오래된 주제라 웬만큼 알려져 있는데, 아직도 자신이 문제를 풀었다며 사재를 털어서 신문에 광고하거나 책을 출간하는 사람들이 있다. 그럴 돈의 100분의 1만 줘도 수학과 대학원생에게서 하루 종일 충분히 설명을 들을 수 있을 텐데, 그럴 생각은 전혀 하지 않는다는 게 내게는 가장 놀라운 점이다.
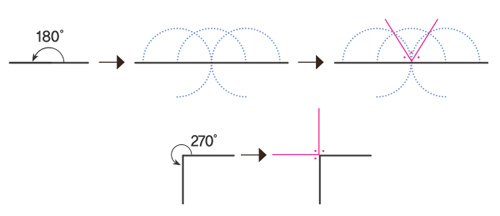
이 문제를 들여다보기 전에 먼저 자와 컴퍼스만 가지고 작도한다는 의미를 정확히 이해해야 한다. 즉 눈금이 없는 자와 컴퍼스 단 두 가지만 사용해 어떤 각도라도 삼등분할 수 있어야 한다는 의미다. 물론 정사각형을 작도할 수 있으니까 270°는 90°로 삼등분할 수 있고 정삼각형을 작도할 수 있으니까 180°도 60°로 삼등분할 수 있다.
자와 컴퍼스만 있으면 각을 계속해서 이등분할 수도 있으니까 135°, 67.5°나 90°, 45°, 22.5°등도 모두 삼등분 작도가 가능하다. 하지만 자와 컴퍼스만 가지고는 삼등분되지 않는 각이 존재하는데, 예를 들면 240°를 삼등분해서 80°를 작도하거나 60°를 삼등분해서 20°를 작도할 수는 없다.
다른 관점에서 보자면 자와 컴퍼스로 정삼각형이나 정사각형을 작도할 수 있기 때문에, 도형의 중심에서 인접한 두 꼭짓점을 이은 두 선이 이루는 각을 둘로 나눠서 정육각형, 정십이각형, 정이십사각형이나 정팔각형, 정십육각형도 작도할 수 있다. 하지만 정칠각형이나 정구각형은 작도할 수 없다. 독일의 수학자 카를 프리드리히 가우스가 생각한 것처럼 작도 가능한 정n각형은n=3,4,5,6,8,10,12,15,16,17,…이고 작도 불가능한 정n각형은 n=7,9,11,13,14,18,19,21,…이다.
각의 삼등분 문제를 삼차방정식으로 푼다
빅토르 위고의 소설 ‘레 미제라블’에도 나오는, 프랑스 혁명의 혼란기에 살았던 천재수학자 에바리스트 갈루아가 시작한 현대 대수학은 각의 삼등분 문제와 삼차방정식을 푸는 문제를 연결시켰다. 간단히 말하자면 코사인 삼배각 공식을 통해서다. 기억이 희미한 독자를 위해 코사인 공식을 적어본다.
예를 들어 3θ=60°라면 cos3θ=1/2이다. 이 경우에 각을 삼등분해서 20°를 작도한다는 것은 cosθ=X라고 놓았을 때 삼차방정식 1/2=4x³-3x를 풀어서 X를 찾아내는 문제로 귀착된다. 물론 X를 구할 수는 있는데, 그 X를 자와 컴퍼스만 가지고 표시할 수 있느냐 하는 것은 또 다른 문제가 된다.
중고등학생 때 신물이 나도록 일차방정식이나 이차방정식을 풀어봤겠지만 삼차방정식 해법은 배우지 않았다는 점을 기억하라. 조금 전에 나온 삼차방정식을 수학 교과서에 배운 수준으로 풀 수 있으면 그 각은 삼등분 가능하고 그렇지 않으면 자와 컴퍼스로는 삼등분이 불가능하다.
예를 들어 180°는 삼등분 가능한데, cos180°=-1 이고 코사인 삼배각 공식에서 얻는 삼차방정식은 -1=4x³-3x이다. 그런데 이 삼차방정식은 고등학생 실력으로 인수분해할 수 있다.
즉 이 삼차방정식은 중고등학교 수준으로 풀리기 때문에 180°는 삼등분 가능하다. 실제로 X=cos(180°/3)=1/2이다.
하지만 60°를 삼등분해 20°를 작도하려면 이번에는 삼차방정식 1/2=4x³-3x을 살펴봐야 하는데, 고등학교 수학으로는 이 방정식을 인수분해할 수 없어서 60°는 삼등분할 수 없다.
예전에 한 번은 엄격한 학술지에서 각을 삼등분하는 주제를 다룬 논문을 게재한 적이 있었다. 논문을 심사한 사람도 편집자도 도저히 논문에서 틀린 곳을 찾아내지 못했기 때문에 논문을 실어줬다. 하지만 알고 보니 그 논문에서 증명한 내용은 각을 셋으로 나누는 게 아니라 세 배로 곱하는 것이어서 수학적으로 전혀 틀린 곳이 없었다는 어처구니없는 일도 있었다.
전 세계 어디나 마찬가지로 우리나라 삼국시대에도 이차방정식이나 일차 연립방정식 정도는 풀 수 있었다. 2000년 전에도 사람들은 삼차방정식을 풀어야 하는 문제를 만들어냈다. 다만 답을 찾아내지 못했을 뿐이다. 예를 들면 아르키메데스는 공을 평면으로 두 조각을 내서 두 조각의 부피 비율이 1대 2가 되려면 어떻게 해야 하느냐고 물었는데, 공의 부피에 대한 공식과 피타고라스 정리를 사용하면 쉽게 삼차방정식이 나온다. 당시 사람들이 그런 평면을 작도하려 했던 것이다.
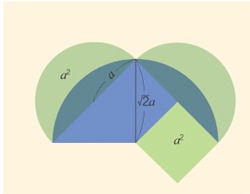
흥미롭게도 초승달 모양과 같은 넓이를 가지는 이등변삼각형은 쉽게 작도할 수 있었다. 여기에서 시작하면 원과 같은 넓이를 가지는 정사각형을 작도하는 문제를 생각하는 것도 상당히 자연스러운 일이다. 이 문제 역시 금방 풀 수 있을 것 같지만 누구도 해결하지 못했다. 지금은 이 문제 역시 작도 불가능하다는 것이 증명됐다. 한편 삼각형과 같은 넓이를 가지는 직사각형을 그리는 문제는 독자를 너무 우습게 보는 것 같으니까 그림만 하나 그려 놓는다.
한상근 교수는 미국 오하이오주립대에서 박사학위를 받고 1989년 KAIST에 부임했다. 정수론과 그 응용인 암호학, 정보학 분야를 연구하고 있다. 1992년 조선시대 수학자 최석정의 저서 ‘구수략’을 접하고 이듬해 ‘최석정과 그의 마방진’이라는 논문을 써 최석정이 조합론 분야의 원조임을 알리는 데 기여했다.
이 기사의 내용이 궁금하신가요?
기사 전문을 보시려면500(500원)이 필요합니다.
2010년 02월 과학동아 정보
글
한상근 KAIST 수학과학과 교수 기자
🎓️ 진로 추천
- 수학
- 물리학
- 교육학