d라이브러리

산불이 번지거나 전염병이 퍼지는 과정을 설명하는 수학이론이 있다. 전파를 매개하는 단위체(나무나 사람) 사이의 연결 정도에 따라 네트워크 형성 여부를 예측하는 침투이론이 그것이다. 수학을 넘어 역학(疫學)과 생태학까지 영역을 넓히는 침투이론이란 무엇일까.

지난 4월 5일 식목일에는 나무를 심는 일보다 식목 과정에서 혹시 일어날지도 모를 산불을 조심하자는 목소리가 더 높았다. 겨울 가뭄으로 나무와 낙엽이 바짝 말라있는 상태에서 나무 한그루를 심고 한숨을 돌리며 입에 문 담배가 나무 수백 수천 그루를 재로 만들어버릴 수도 있기 때문이다.

지난 2005년 양양 낙산사를 전소시킨 산불도 어딘가에 버려진 담배꽁초에서 시작했을 가능성이 높다. 우리나라 산처럼 나무가 빽빽한 숲에서는 한 지점에서 불이 시작되면 주위로 불이 번질 가능성이 크다. 육상 경기에 비유하자면 나무는 불을 전달하는 릴레이 주자인 셈이다. 만일 낙산사 주변에 나무들이 울창하지 않았다면 낙산사는 화마를 피할 수 있었을 것이다.

그렇다면 애초에 나무를 띄엄띄엄 심는다면 설사 한 곳에 불이 나더라도 산불로 이어지지는 않지 않을까. 적어도 불이 번지는 속도를 늦출 수 있을 것이다. 실제로 식목 밀도에 따른 산불 진행 여부를 예측할 수 있는 수학이론이 있다. 침투이론(percolation theory)이 그것이다. 침투이론은 산불이 번지는 현상 뿐 아니라 모래에 빗물이 스며드는 과정을 설명한다. 또 전염병 전파도 침투이론의 적용 대상이다. 최근에는 메뚜기가 떼를 짓는 과정도 침투현상으로 설명하고 있다.


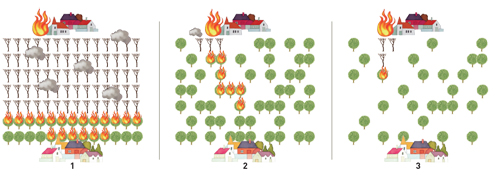
산불 전파의 침투이론
윗마을에서 불이 났을 때 중간 숲을 지나 아랫마을로 불이 옮을 것인가를 자리 침투이론으로 설명했다. 일정한 간격(격자)의 나무 사이에만 불이 옮을 수 있다고 가정하면 격자에 나무가 있을 확률(p)에 따라 불의 번짐 여부가 결정되는데 그 분기점이 임계확률(pc)이다. p가 pc 보다 크면 전체 네트워크로 불이 번져(침투) 아랫마을을 덮치고(1), pc 일 때는 반반이다(.). pc보다 작으면 얼마 못가 불이 꺼진다(2).

연결 정도 어느 선 넘으면 전체로 퍼져
침투이론은 네트워크를 이루고 있는 단위체(클러스터) 사이의 연결 정도가 네트워크 형성 여부에 미치는 영향에 대해 연구하는 분야다. 산불의 경우 나무를 단위체로 볼 수 있다. 단위체 사이의 연결성을 수학적으로 설명하기 위해서는 이들 배열을 단순화할 필요가 있다. 즉 벌집 같은 격자 안에 나무가 한 그루가 있고 인접한 격자(6개)에 나무가 있을 경우 불이 옮을 수 있고 나무가 없다면 더 이상 번지지 않는다고 가정해보자.

만일 어떤 격자 안의 나무에 불이 났는데 위쪽과 아래쪽 격자 안에 나무가 심어져 있다면 불은 위쪽과 아래쪽으로 번질 것이다. 주변 격자 어디에도 나무가 없다면 불은 나무 한 그루만 태우고 꺼질 것이다. 이처럼 인접 격자 안에 나무가 있을 평균 확률을 p라고 할 때 산 전체로 불이 번지려면 p 값은 얼마가 돼야 할까.

p=0, 즉 주변 격자에 나무가 없다면 당연히 불은 번지지 않을 것이다. 그렇다면 p=1/3, 즉 인근 격자 안에 나무가 있을 평균 확률이 1/3일 때는 어떻게 될까. 이 경우 평균적으로 격자 6곳 가운데 2곳에 나무가 있을 것이다. 물론 평균 확률이므로 주변 격자에 나무가 전혀 없는 경우도 있고 6곳 다 있을 수도 있다. 수학자들은 산이 무한히 넓다고 가정하고 p의 값에 따른 산불의 번짐 여부, 즉 전체 네트워크의 형성 가능성을 조사했다.

그 결과 p가 0.5 미만일 때는 불이 번지다 어느 지점에서 연결이 끊겨 소멸됐다. 물론 p=0.2일 때보다는 p=0.4일 때 더 넓은 지역이 불탄다. 한편 p값이 0.5를 넘으면 불은 산 전체로 번진다. p=0.6일 때보다는 p=0.8일 때 불이 더 빨리 번지고 불타지 않고 남아 있는 (네트워크에 연결되지 않은) 나무의 비율이 훨씬 낮다. 1982년 미국 코넬대 수학과 해리 케스텐 교수는 이 같은 2차원 격자의 경우 불이 전체로 번지는, 즉 침투하기 시작하는 임계확률이 0.5임을 증명했다. 우리나라 산에는 나무들이 너무 빽빽하게 들어차 있기 때문에 p값은 1에 가깝다고 볼 수 있다. 일단 불이 붙으면 성공적으로 진화하지 못하는 한 산 전체가 잿더미가 되는 이유다.

산불 모형처럼 격자 안에 단위체 유무에 따라서 침투여부가 결정되는 방식을 ‘자리 침투’(site percolation)라고 한다. 또 다른 침투 방식으로는 ‘결합 침투’(bond percolation)가 있다. 여기서는 모든 격자 안에 단위체가 있고 대신 격자 사이에 연결, 즉 결합 여부가 확률적으로 정해졌을 때 계에 침투가 일어나는지 여부를 예측하는 이론이다.

예를 들어 벌집 모양의 격자 안에 오리농장이 하나씩 있다고 하자. 6각형이므로 오리농장 1곳은 6곳의 오리농장과 인접해 있다. 농장 위를 지나가던 철새가 똥을 쌌는데 마침 오리 한 마리한테 떨어져 농장에 조류독감이 퍼졌다고 하자. 농장주가 아직 이 사실을 모른다면 외부와 왕래를 하면서(결합된 상태) 인근 농장 6곳으로 조류독감이 퍼질 것이다. 어느 순간 정부가 사태를 파악하면 방역에 들어가 감염된 농장들을 격리시킨다(인근 농장들과 결합을 끊는다). 그렇다면 어느 정도 결합을 끊어야 조류독감이 전국으로 퍼지는, 즉 침투하는 상황을 막을 수 있을까.

얼핏 생각하면 감염된 농장들을 완전히 격리시켜야할 것 같다. 즉 인근 6개 농장 가운데 한곳이라도 바이러스가 퍼지면 결국은 전국으로 번지지 않을까. 1981년 수학자 비어만은 인접 농장과 결합할 확률이 2sin(π/18)(약 0.347) 미만일 경우 침투가 일어나지 않음을 증명했다. 즉 방역이 불완전해 인근 농장 한 두 곳으로 바이러스가 퍼지더라도 결국에는 어느 선에서 확산이 멈춘다는 것.

질병 확산 패턴도 설명
이처럼 침투이론은 질병의 확산을 설명하는데도 유용한 도구가 될 수 있다. 질병 확산에 침투이론을 성공적으로 적용한 예로 식물을 감염시키는 곰팡이의 전파에 대한 연구결과가 있다. 식물은 움직이지 않기 때문에 실제 상황을 재현한 수학 모델을 만들기 쉽다. 영국 케임브리지대 식물과학과 윌프레드 오텐 교수팀은 벼나 옥수수에서 잎집무늬마름병을 일으키는 곰팡이인 라이족토니아(Rhizoctonia solani)의 확산 패턴을 침투이론으로 설명해 2004년 식물학 저널인 ‘뉴 피톨로지스트’에 발표했다.

라이족토니아는 균사를 통해 퍼져나간다. 연구자들은 샬레를 벌집 같은 격자로 나눠 격자마다 영양분을 떨어뜨린 뒤 한 지점에 곰팡이를 접종했다. 곰팡이는 옆의 격자로 균사를 뻗어내며 샬레 전체로 퍼져나갔다. 대조군으로 격자의 일정 비율을 무작위로 골라 영양분을 뺀 샬레를 준비했다. 연구자들은 영양분이 있는 격자의 비율을 10% 단위로 낮추면서 확산 패턴을 관찰했다. 그 결과 격자의 60%에 영양분이 있을 때까지는 샬레 전체로 곰팡이가 확산됐지만(침투 성공) 50%가 되자 실험에 따라 전체로 퍼지기도 하고 제한된 범위 안에서 멈추기도 했다. 40% 부터는 전체로 퍼지는데 실패했다. 수학 모델(자리 침투이론)과 일치하는 결과가 나온 셈이다.

한편 영양분이 있는 격자 비율이 50%가 넘어 곰팡이가 전체로 퍼지는 걸 막지 못하는 경우도 비율이 낮을수록 확산 속도는 상당히 늦어진다는 게 확인됐다. 연구자들은 “병이 퍼져나가는 건 호수에 돌을 떨어뜨렸을 때 물결이 사방으로 퍼지는 것과 같다”며 “중간 중간에 매개체가 없을 경우 병목현상이 일어나 전파가 지연된다”고 설명했다.

이런 연구 결과는 농업현장에서 응용될 수 있다. 넓은 땅에 한 가지 농작물만 심을 경우 경작은 효율적이겠지만 질병확산에 취약할 수 있다. 따라서 모자이크처럼 여러 작물을 교대로 심어 병원체가 경작지 전체로 침투하는 걸 막거나 늦출 수 있다. 최근에는 질병 전파 뿐 아니라 동물의 행동 양식을 설명하는데도 침투이론이 쓰인다.

메뚜기는 타고난 수학자?
가끔씩 해외뉴스를 보면 메뚜기가 구름처럼 떼를 이뤄 농작물을 초토화시키는 장면이 나온다. 도대체 이 많은 메뚜기들은 어디서 왔을까. 호주 시드니대 수리생물학센터 스테펜 심프슨 교수팀은 메뚜기의 분포 밀도가 일정 수준이상 올라가면 단독생활에서 떼를 이루는 쪽으로 생태를 바꾸는 과정을 침투이론으로 설명했다. 이번에는 격자(서로 가까이 있는 나무나 풀) 안의 메뚜기들이 단위체가 되고 도마뱀 같은 메뚜기 천적의 활동범위가 네트워크가 된다.

포식자는 먹이를 잡을 때 들어가는 에너지보다 먹이에서 얻는 게 많아야 성공적으로 살아나간다. 만일 일정 범위 안의 메뚜기들을 잡아먹어 그 수가 이런 수준 이하로 떨어지면 도마뱀이 주변의 다른 영역, 즉 격자로 이동한다. 그런데 여기에도 메뚜기 밀도가 낮을 경우에는 살아가는데 어려움을 겪게 된다.

만일 주변에 충분한 수의 메뚜기가 있다면 계속 격자를 옮겨가며 먹이를 손쉽게 사냥할 수 있다. 메뚜기의 입장에서는 최악의 상황인 셈이다. 따라서 메뚜기의 밀도가 어느 수준 이상이 돼 천적의 침투 네트워크가 가능할 경우는 오히려 메뚜기들이 한 곳으로 몰려 집단을 이루는 게 생존에 더 유리하다. 연구자들은 “좁은 지역에 극단적인 밀도로 메뚜기가 모이면 포식자의 먹이 네트워크의 연결성이 없어지는 결과를 낳는다”며 “또 무리가 어느 방향으로 이동할 지 예측할 수 없다는 점도 포식자를 힘들게 한다”고 설명했다.
결국 메뚜기는 서식 밀도가 낮을 때는 개별적으로 살아가고 밀도가 높아지면 떼를 이룸으로써 주어진 상황에서 최선의 선택을 하는 셈이다.