구독상품안내
과학영재학교와 과학고 입시에서 창의적 문제해결력 검사의 비중이 커지고 문제 유형 또한 바뀌고 있다. 출제가능성이 높은 예상문제를 풀어보면서 실전감각을 길러두자.
수학
바둑판 모양의 10×10 보드가 주어져 있을 때 아래 질문에 답하시오.
1) 1×1 블록을 제거해 보드 위에 2×1 블록이 존재하지 않도록 하려고 한다. 제거해야 하는 1×1 블록은 최소 몇 개인가?
2) 1×1 블록을 제거해 보드 위에 2×2 블록이 존재하지 않도록 하려고 한다. 제거해야 하는 1×1 블록은 최소 몇 개인가?
3) 1×1 블록을 제거해 보드 위에 3×2 블록이 존재하지 않도록 하려고 한다. 제거해야 하는 1×1 블록은 최소 몇 개인가?
예시답안
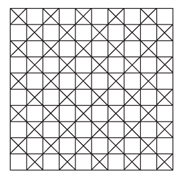1) 10×10 보드를 2×1 블록으로 나누면 50개의 블록이 나오는데, 각각의 2×1 블록에서 적어도 한 개의 1×1 블록을 제거해야 한다. 제거할 1×1 블록의 개수는 50개. 아래 그림처럼 X친 1×1 블록을 제거하면 2×1 블록이 존재하지 않으므로 답은 50개다.
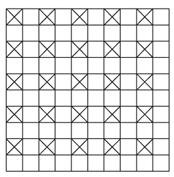2) 10×10 보드를 2×2 블록으로 나누면 25개의 블록이 나오게 되는데, 각각의 2×2 블록에서 적어도 한 개의 1×1 블록을 제거해야 한다. 따라서 1×1 블록은 적어도 25개 제거해야 한다. 아래 그림처럼 X친 1×1 블록을 제거하면 2×2 블록이 존재하지 않으므로 답은 25개다.
3) 5×5 보드에서 1×1 블록을 최소한 4개 이하로 제거해 3×2 블록이 존재하지 않게 하려면 아래 왼쪽 그림과 같이 테두리 부분에 있는 정사각형을 제거하지 말아야 한다.
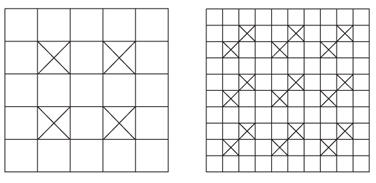
따라서 5×10 보드에서는 1×1 블록을 8개 이상 제거해야 3×2 블록이 존재하지 않게 된다. 실제로 5×10 보드에서 3×2 블록이 존재하지 않으려면 1×1 정사각형을 9개 이상 제거해야 하고 10×10 보드에서는 18개 이상 제거해야 한다.
그림처럼 X친 부분의 정사각형을 제거하면 3×2 블록이 존재하지 않으므로 답은 18개다.
과학
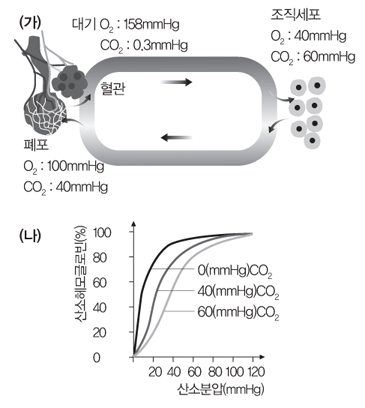
1. 그림 (가)는 혈액순환과정에서 기체의 분압을 나타낸 그림이고, 그림 (나)는 산소해리곡선이다.
1) 호흡과정에서 폐포와 모세혈관, 조직세포와 모세혈관 사이에서 기체의 교환 원리는 무엇인가?
2) 폐포에서 받은 산소를 세포까지 운반하는 물질은 무엇인가?
3) 위 그림에 따르면 폐포에서 운반해온 산소 중에서 적어도 몇 %가 세포에게 제공되겠는가?
예시답안
1) 각 기체는 분압차이에 의한 확산으로 교환된다.
2) 산소는 폐포 근처에서 적혈구의 헤모글로빈과 결합해 조직세포까지 혈액과 함께 이동하고, 조직세포 근처에서는 헤모글로빈에서 해리돼 세포로 확산된다.
3) 폐포에서의 산소 분압은 100mmHg, 이산화탄소 분압은 40mmHg이므로 산소헤로글로빈의 포화도는 100%이다. 한편 조직세포에서는 산소분압이 40mmHg이고 이산화탄소분압은 60mmHg이다. 그래프 (나)에서 조직세포 근처에서는 산소헤모글로빈 포화도가 60%이므로 운반되온 산소의 40%의 산소만 세포에게 제공된다.
2. 다음은 암모니아 기체에 관한 실험이다. 잘 읽고 물음에 답하시오.
1) 플라스크 내의 물은 왜 빨갛게 변하는가?
2) 처음에 스포이트를 눌러 물 한 방울을 플라스크 안에 넣어 주는 이유는 비커에 있는 물이 플라스크로 빨려 올라가도록 하기 위함이다. 물이 충분히 빨려 올라가면 플라스크에서 붉은 물이 분수처럼 쏟아지는데 이는 암모니아의 어떤 성질을 이용한 것인지 간단히 쓰시오.
3) 물이 분수처럼 쏟아지는 현상이 계속된다면 플라스크 내부의 압력과 대기압의 관계는 어떻게 변하는지 간단하게 쓰시오.
예시답안
1) 암모니아가 물에 녹으면서 염기성 용액이 됐기 때문이다. 페놀프탈레인 용액은 염기성에서 붉은색을 띈다.
2) 한 방울의 물에도 암모니아가 잘 녹기 때문에 압력의 차가 크게나서 반응이 지속적으로 일어난다. 또한 유리관의 입구가 작기 때문에 물이 흐르지 않고 분수처럼 쏟아진다.
3) 플라스크의 안의 암모니아 기체가 물에 녹아들어가므로 녹은 기체만큼 내부 압력이 낮아진다.
3. 롤러코스터가 높이 h인 점 P에서 출발해 반지름이 r인 원형의 레일을 돌려고 한다. 롤러코스터는 질량이 m인 객차 세 개로 구성돼 있다.
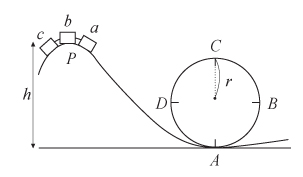
다음 물음에 답하시오 (단, 롤러코스터를 인위적으로 움직이는 동력원은 없고 객차와 레일 사이의 마찰은 무시한다. 중력 가속도는 g이다).
1) 객차 b가 점 P를 출발하는 순간을 t1, 객차 c가 점 P를 지나가는 순간을 t2, 객차 a가 점 A를 지나는 순간을 t3, 객차 b가 점 A를 지나는 순간을 t4라고 할 때, 다음 보기의 에너지 크기를 비교하고 그 이유를 설명하시오.
① t1일 때 롤러코스터의 위치 에너지
② t2일 때 롤러코스터의 위치 에너지
③ t3일 때 롤러코스터의 운동 에너지
④ t4일 때 롤러코스터의 운동 에너지
2) 롤러코스터를 하나의 질점으로 생각할 때, 롤러코스터가 무사히 도착점에 도달하기 위한 최소의 h는 r의 몇 배인가?
예시답안
1) 먼저 롤러코스터가 t1일 때 세 객차의 질량 중심의 연직 위치를 파악해보자. a, c가 같은 높이에 있다면, 질량 중심의 정의에 의해 b의 높이(질량 m)와 a, c(질량 2m)의 높이를 2:1로 내분한 높이가 세 객차의 질량 중심의 높이가 된다. t2일 때는 b의 위치이며, t3일 때는 b의 위치, t4일 때는 b의 높이와 a, c의 높이를 2:1로 내분하는 점이다.
역학적 에너지가 보존된다면 t1에서는 위치 에너지가, t4에서는 운동 에너지가 각각 최댓값이고 그 크기가 같다. t2에서 꼭대기로부터의 높이차와 t3에서 바닥으로부터의 높이차가 같으므로 t2에서의 위치 에너지와 t3에서의 운동 에너지는 같다. 그러므로 정답은 ① = ④ > ② = ③.
2) 역학적 에너지가 보존돼 C점에서 레일과 주고받는 수직항력(N)이 존재하면 C점을 무사히 통과할 수 있다. 그러므로 다음과 같은 식이 성립한다.
수학
바둑판 모양의 10×10 보드가 주어져 있을 때 아래 질문에 답하시오.
1) 1×1 블록을 제거해 보드 위에 2×1 블록이 존재하지 않도록 하려고 한다. 제거해야 하는 1×1 블록은 최소 몇 개인가?
2) 1×1 블록을 제거해 보드 위에 2×2 블록이 존재하지 않도록 하려고 한다. 제거해야 하는 1×1 블록은 최소 몇 개인가?
3) 1×1 블록을 제거해 보드 위에 3×2 블록이 존재하지 않도록 하려고 한다. 제거해야 하는 1×1 블록은 최소 몇 개인가?
예시답안
1) 10×10 보드를 2×1 블록으로 나누면 50개의 블록이 나오는데, 각각의 2×1 블록에서 적어도 한 개의 1×1 블록을 제거해야 한다. 제거할 1×1 블록의 개수는 50개. 아래 그림처럼 X친 1×1 블록을 제거하면 2×1 블록이 존재하지 않으므로 답은 50개다.2) 10×10 보드를 2×2 블록으로 나누면 25개의 블록이 나오게 되는데, 각각의 2×2 블록에서 적어도 한 개의 1×1 블록을 제거해야 한다. 따라서 1×1 블록은 적어도 25개 제거해야 한다. 아래 그림처럼 X친 1×1 블록을 제거하면 2×2 블록이 존재하지 않으므로 답은 25개다.3) 5×5 보드에서 1×1 블록을 최소한 4개 이하로 제거해 3×2 블록이 존재하지 않게 하려면 아래 왼쪽 그림과 같이 테두리 부분에 있는 정사각형을 제거하지 말아야 한다.
따라서 5×10 보드에서는 1×1 블록을 8개 이상 제거해야 3×2 블록이 존재하지 않게 된다. 실제로 5×10 보드에서 3×2 블록이 존재하지 않으려면 1×1 정사각형을 9개 이상 제거해야 하고 10×10 보드에서는 18개 이상 제거해야 한다.
그림처럼 X친 부분의 정사각형을 제거하면 3×2 블록이 존재하지 않으므로 답은 18개다.
과학
1. 그림 (가)는 혈액순환과정에서 기체의 분압을 나타낸 그림이고, 그림 (나)는 산소해리곡선이다.
1) 호흡과정에서 폐포와 모세혈관, 조직세포와 모세혈관 사이에서 기체의 교환 원리는 무엇인가?
2) 폐포에서 받은 산소를 세포까지 운반하는 물질은 무엇인가?
3) 위 그림에 따르면 폐포에서 운반해온 산소 중에서 적어도 몇 %가 세포에게 제공되겠는가?
예시답안
1) 각 기체는 분압차이에 의한 확산으로 교환된다.
2) 산소는 폐포 근처에서 적혈구의 헤모글로빈과 결합해 조직세포까지 혈액과 함께 이동하고, 조직세포 근처에서는 헤모글로빈에서 해리돼 세포로 확산된다.
3) 폐포에서의 산소 분압은 100mmHg, 이산화탄소 분압은 40mmHg이므로 산소헤로글로빈의 포화도는 100%이다. 한편 조직세포에서는 산소분압이 40mmHg이고 이산화탄소분압은 60mmHg이다. 그래프 (나)에서 조직세포 근처에서는 산소헤모글로빈 포화도가 60%이므로 운반되온 산소의 40%의 산소만 세포에게 제공된다.
2. 다음은 암모니아 기체에 관한 실험이다. 잘 읽고 물음에 답하시오.
1) 플라스크 내의 물은 왜 빨갛게 변하는가? 2) 처음에 스포이트를 눌러 물 한 방울을 플라스크 안에 넣어 주는 이유는 비커에 있는 물이 플라스크로 빨려 올라가도록 하기 위함이다. 물이 충분히 빨려 올라가면 플라스크에서 붉은 물이 분수처럼 쏟아지는데 이는 암모니아의 어떤 성질을 이용한 것인지 간단히 쓰시오.
3) 물이 분수처럼 쏟아지는 현상이 계속된다면 플라스크 내부의 압력과 대기압의 관계는 어떻게 변하는지 간단하게 쓰시오.
예시답안
1) 암모니아가 물에 녹으면서 염기성 용액이 됐기 때문이다. 페놀프탈레인 용액은 염기성에서 붉은색을 띈다.
2) 한 방울의 물에도 암모니아가 잘 녹기 때문에 압력의 차가 크게나서 반응이 지속적으로 일어난다. 또한 유리관의 입구가 작기 때문에 물이 흐르지 않고 분수처럼 쏟아진다.
3) 플라스크의 안의 암모니아 기체가 물에 녹아들어가므로 녹은 기체만큼 내부 압력이 낮아진다.
3. 롤러코스터가 높이 h인 점 P에서 출발해 반지름이 r인 원형의 레일을 돌려고 한다. 롤러코스터는 질량이 m인 객차 세 개로 구성돼 있다.
다음 물음에 답하시오 (단, 롤러코스터를 인위적으로 움직이는 동력원은 없고 객차와 레일 사이의 마찰은 무시한다. 중력 가속도는 g이다).
1) 객차 b가 점 P를 출발하는 순간을 t1, 객차 c가 점 P를 지나가는 순간을 t2, 객차 a가 점 A를 지나는 순간을 t3, 객차 b가 점 A를 지나는 순간을 t4라고 할 때, 다음 보기의 에너지 크기를 비교하고 그 이유를 설명하시오.
① t1일 때 롤러코스터의 위치 에너지
② t2일 때 롤러코스터의 위치 에너지
③ t3일 때 롤러코스터의 운동 에너지
④ t4일 때 롤러코스터의 운동 에너지
2) 롤러코스터를 하나의 질점으로 생각할 때, 롤러코스터가 무사히 도착점에 도달하기 위한 최소의 h는 r의 몇 배인가?
예시답안
1) 먼저 롤러코스터가 t1일 때 세 객차의 질량 중심의 연직 위치를 파악해보자. a, c가 같은 높이에 있다면, 질량 중심의 정의에 의해 b의 높이(질량 m)와 a, c(질량 2m)의 높이를 2:1로 내분한 높이가 세 객차의 질량 중심의 높이가 된다. t2일 때는 b의 위치이며, t3일 때는 b의 위치, t4일 때는 b의 높이와 a, c의 높이를 2:1로 내분하는 점이다.
역학적 에너지가 보존된다면 t1에서는 위치 에너지가, t4에서는 운동 에너지가 각각 최댓값이고 그 크기가 같다. t2에서 꼭대기로부터의 높이차와 t3에서 바닥으로부터의 높이차가 같으므로 t2에서의 위치 에너지와 t3에서의 운동 에너지는 같다. 그러므로 정답은 ① = ④ > ② = ③.
2) 역학적 에너지가 보존돼 C점에서 레일과 주고받는 수직항력(N)이 존재하면 C점을 무사히 통과할 수 있다. 그러므로 다음과 같은 식이 성립한다.
